User:
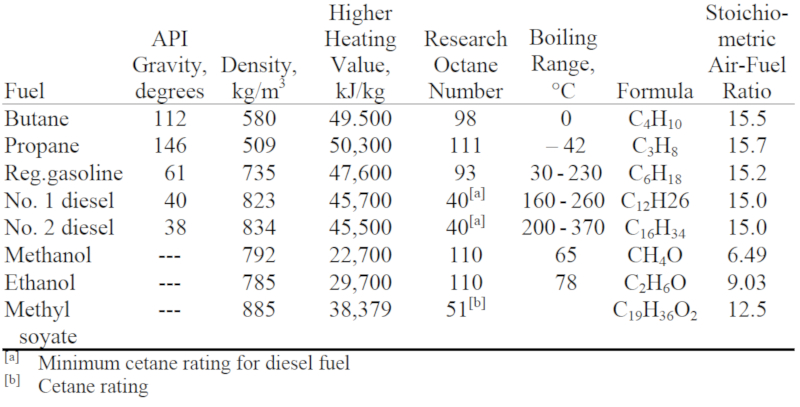
Technical Solution
Concept 
The Otto engine operates in two cycles: the actual Otto cycle, which consists of the following phases:
• Phase 1 to 2: Adiabatic compression
• Phase 2 to 3: Heating
• Phase 3 to 4: Adiabatic expansion
• Phase 4 to 1: Cooling
In addition, it has a cycle for emptying the burnt gases and filling with a fresh mixture.
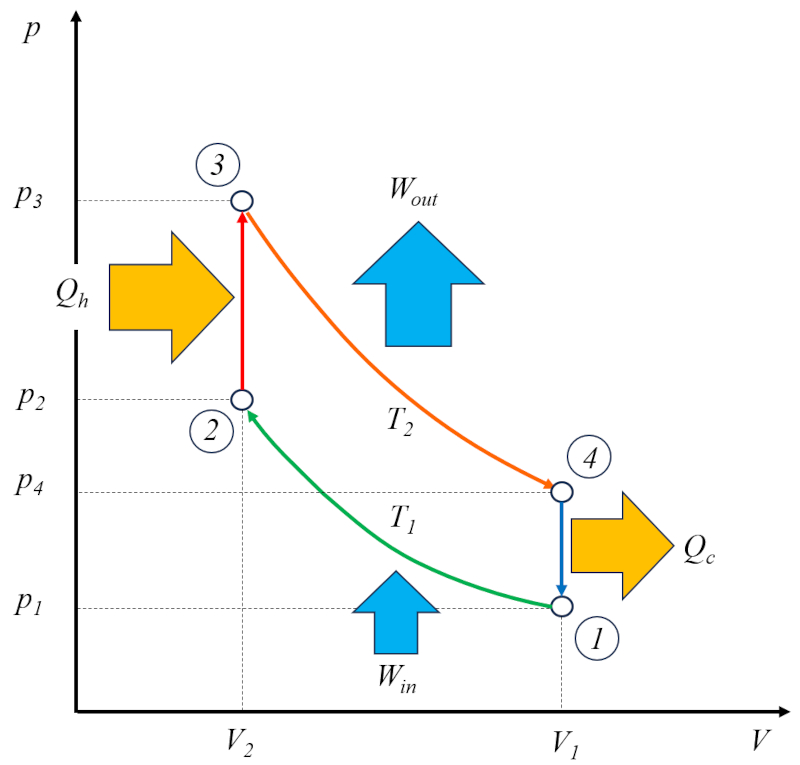
For this reason, it is referred to as a two-stroke engine. The emptying and filling phase can be accomplished using a compensating mass or through a second cylinder that operates out of phase.
The efficiency the efficiency ($\eta$) of the engine can be estimated using the otto compressibility factor ($r$) and the adiabatic index ($\kappa$) with the following equation:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Compressibility factor $r$
Equation
The efficiency ($\eta$) is ultimately a function of the expanded volume ($V_1$) and the compressed volume ($V_2$), and in particular, of the otto compressibility factor ($r$):
 $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Adiabatic expansion is described using the variables the adiabatic index ($\kappa$), the temperature in state 4 ($T_4$), the temperature in state 3 ($T_3$), the expanded volume ($V_1$), and the compressed volume ($V_2$) through the relationship
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
While adiabatic compression is represented by the temperature in state 1 ($T_1$) and the temperature in state 2 ($T_2$) through the relationship
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
By subtracting the second equation from the first, we obtain
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Which leads us to the relationship
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
And this allows us to define the otto compressibility factor ($r$) as follows:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
ID:(11162, 0)
Efficiency depending on the compressibility factor
Equation
The efficiency ($\eta$) can be calculated from the otto compressibility factor ($r$) and the adiabatic index ($\kappa$) in the case of the Otto cycle using:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
The efficiency ($\eta$), in terms of the temperature in state 1 ($T_1$), the temperature in state 2 ($T_2$), the temperature in state 3 ($T_3$), and the temperature in state 4 ($T_4$), is calculated using the equation:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
In the case of adiabatic expansion, it is described using the adiabatic index ($\kappa$), the expanded volume ($V_1$), and the compressed volume ($V_2$) with the relationship:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
And adiabatic compression is represented by the relationship:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
If we subtract the second equation from the first, we obtain:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Which leads to the relationship:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
This, in turn, leads to the definition of the otto compressibility factor ($r$) with the equation:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
With all these components, the efficiency of a process using the Otto cycle can be calculated as:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
.
ID:(11163, 0)