Utilizador:
Fluxo de Água
Storyboard 
Em solo saturado, podem ocorrer situações em que ocorram variações de pressão. Essas variações, por sua vez, geram um fluxo que, neste caso, deve ocorrer dentro dos poros do solo. Como esses poros têm uma ordem de tamanho da ordem de micrômetros ou dezenas de micrômetros, o fluxo tende a ser laminar devido aos baixos números de Reynolds.
ID:(369, 0)
Solução de densidade de fluxo de um canal
Imagem
A solução obtida para a altura e os parâmetros o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) nos mostra que la densidade de fluxo ($j_s$) é igual a:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Podemos representar la densidade de fluxo ($j_s$) graficamente em termos dos fatores adicionais $j_s/j_{s0}$ e $x/x_0$ da seguinte maneira:
la densidade de fluxo ($j_s$) continua aumentando à medida que nos aproximamos do canal, à medida que la altura da coluna d'água no solo ($h$) diminui. Esse aumento é necessário para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, aumentá-la.
ID:(7827, 0)
Fluxo laminar através de um tubo
Nota
Quando um tubo preenchido com líquido de viscosidade ERROR:5422,0 é exposto a la pressão na posição inicial ($p_i$) em o posição no início do tubo ($L_i$) e la pressão na posição final (e) ($p_e$) em o posição na extremidade do tubo ($L_e$), gera-se uma diferença de pressão ($\Delta p_s$) ao longo de o comprimento do tubo ($\Delta L$), resultando no perfil de la velocidade em um raio do cilindro ($v$):
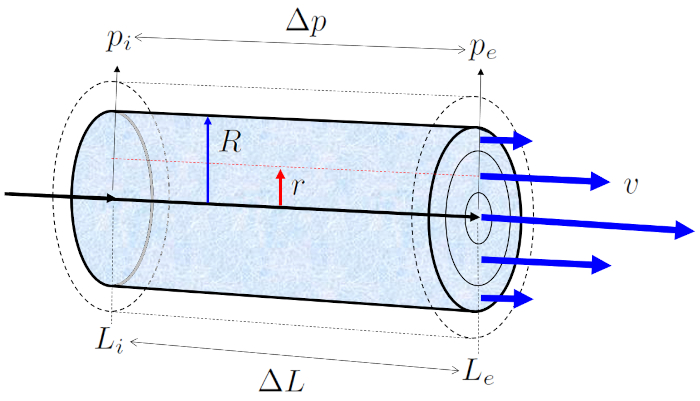
Em fluxos com valores baixos de o número de Reynolds ($Re$), onde a viscosidade é mais relevante do que a inércia do líquido, o fluxo se desenvolve de forma laminar, ou seja, sem a presença de turbulência.
ID:(2218, 0)
Folhas no córrego
Citar
No fluxo laminar, camadas adjacentes se movem e existe uma força gerada pela viscosidade entre elas. A camada mais rápida arrasta sua vizinha mais lenta, enquanto a mais lenta restringe o avanço da mais rápida.
Portanto, a força la força viscosa ($F_v$) gerada por ERROR:10119.1 sobre a outra é uma função de ERROR:5556.1, ERROR:5436.1 e ERROR:5422.1, como mostrado na seguinte equação:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
ilustrado no seguinte diagrama:
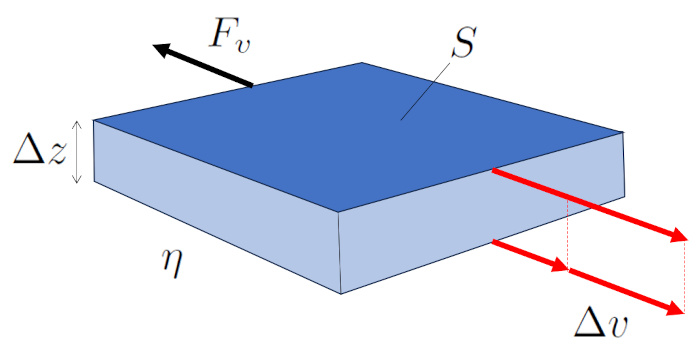
ID:(7053, 0)
Fluir através de um cilindro
Exercício
O fluxo laminar ao redor de um cilindro pode ser representado como múltiplas camadas cilíndricas deslizando sob a influência das camadas adjacentes. Nesse caso, la força viscosa ($F_v$) com o comprimento do tubo ($\Delta L$), la viscosidade ($\eta$) e as variáveis la posição radial no cilindro ($r$) e la velocidade em um raio do cilindro ($v$) é expresso como:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
A camada na borda em ERROR:5417.1 permanece estacionária devido ao efeito de borda e, através de la viscosidade ($\eta$), retarda a camada adjacente que possui velocidade.
O centro é a parte que se move em la taxa de fluxo máxima ($v_{max}$), arrastando a camada circundante. Por sua vez, essa camada arrasta a próxima e assim por diante até atingir a camada em contato com a parede do cilindro, que está estacionária.
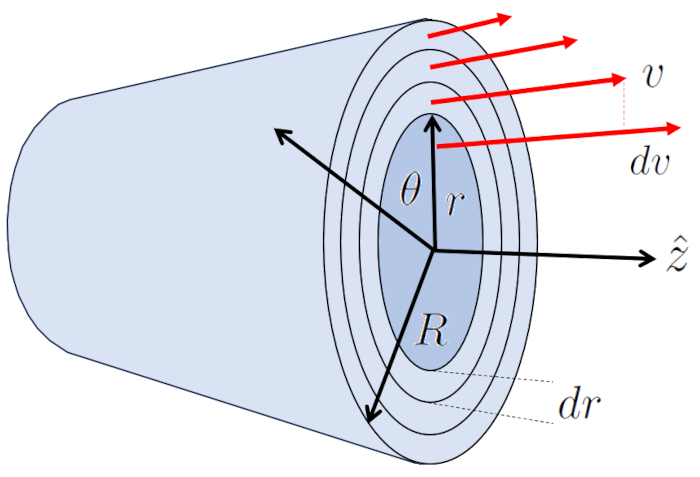
Dessa forma, o sistema transfere energia do centro para a parede, gerando um perfil de velocidade representado por:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
com:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Fluxo de acordo com a equação de Hagen-Poiseuille
Equação
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo através da integração de toda a superfície, o que nos leva à conhecida lei de Hagen-Poiseuille.
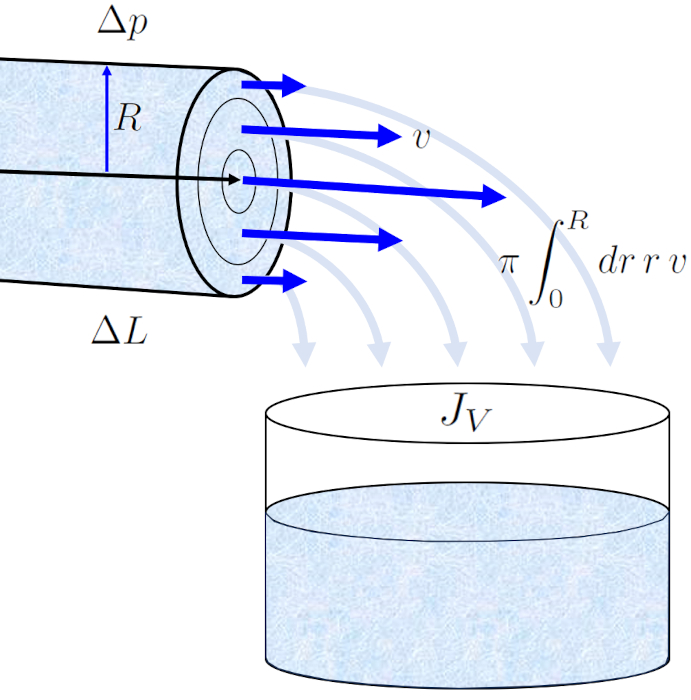
O resultado é uma equação que depende de ERROR:5417,0 elevado à quarta potência. No entanto, é fundamental observar que este perfil de fluxo só é válido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ERROR:6673,1, a expressão:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre as leis que regem o fluxo da água em recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Pesquisa experimental sobre o movimento de líquidos em tubos de diâmetros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Fluxo de volume
Script
Durante um tempo decorrido ($\Delta t$), o fluido com uma velocidade média do fluido ($v$) se desloca um elemento de tubo ($\Delta s$). Se la seção ($S$) representa a quantidade de fluido que atravessa essa seção em o tempo decorrido ($\Delta t$), é calculada como:
$\Delta V = S \Delta s = Sv \Delta t$
Esta equação indica que o volume de fluido que flui através da seção la seção ($S$) durante um tempo decorrido ($\Delta t$) é igual ao produto da área da seção e a distância percorrida pelo fluido nesse tempo.
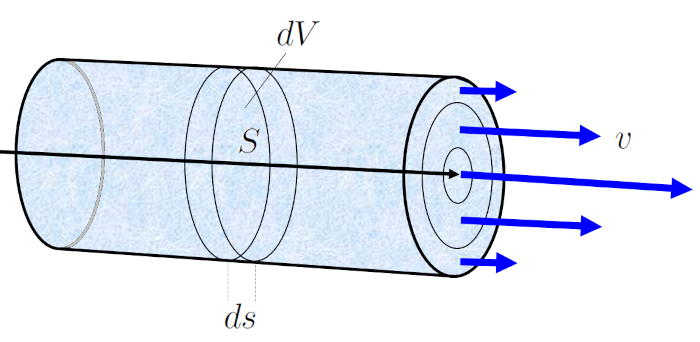
Isso facilita o cálculo de o elemento de volume ($\Delta V$), que é o volume de fluido que flui pelo canal em um período específico de o tempo decorrido ($\Delta t$), correspondente a o fluxo de volume ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Fluxo de Água
Storyboard
Em solo saturado, podem ocorrer situações em que ocorram variações de pressão. Essas variações, por sua vez, geram um fluxo que, neste caso, deve ocorrer dentro dos poros do solo. Como esses poros têm uma ordem de tamanho da ordem de micrômetros ou dezenas de micrômetros, o fluxo tende a ser laminar devido aos baixos números de Reynolds.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Se examinarmos la condutância hidráulica ($G_h$), podemos notar que o numerador cont m a rea da se o transversal do tubo, representada como $\pi R^2$. Aqui, o raio do tubo ($R$) corresponde a uma propriedade do l quido, la viscosidade ($\eta$) est relacionada viscosidade do fluido, e o comprimento do tubo ($\Delta L$) refere-se ao gradiente de press o gerado.
Assim, o fator espec fico da geometria dos poros pode ser definido como la permeabilidade hidrodinâmica ($k$) usando a seguinte f rmula:
Se considerarmos o perfil de ERROR:5449,0 para um fluido em um canal cil ndrico, onde la velocidade em um raio do cilindro ($v$) varia em rela o a ERROR:10120,0 de acordo com a seguinte express o:
envolvendo o raio do tubo ($R$) e la taxa de fluxo máxima ($v_{max}$). Podemos calcular la taxa de fluxo máxima ($v_{max}$) utilizando la viscosidade ($\eta$), la diferença de pressão ($\Delta p$) e o comprimento do tubo ($\Delta L$) da seguinte forma:
Se integrarmos a velocidade em toda a se o transversal do canal, obteremos o fluxo de volume ($J_V$), definida como a integral de $\pi r v(r)$ em rela o a ERROR:10120,0 de $0$ a ERROR:5417,0. Essa integral pode ser simplificada da seguinte maneira:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
A integra o resulta na lei de Hagen-Poiseuille resultante:
O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equa o:
Al m disso, usando a rela o para la resistência hidráulica ($R_h$):
obt m-se o resultado:
Como a for a viscosa
e a superf cie do cilindro
$S=2\pi R L$
onde $R$ o raio e $L$ o comprimento do canal, a for a viscosa pode ser expressa como
onde $\eta$ representa a viscosidade e $dv/dr$ o gradiente de velocidade entre a parede e o fluxo.
Quando uma la diferença de pressão ($\Delta p_s$) age sobre uma se o com uma rea de $\pi R^2$, com o raio do tubo ($R$) como o raio de curvatura ($r$), ela gera uma for a representada por:
$\pi r^2 \Delta p$
Essa for a impulsiona o l quido contra a resist ncia viscosa, dada por:
Ao igualarmos essas duas for as, obtemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
O que nos leva equa o:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Se integrarmos essa equa o de uma posi o definida por o raio de curvatura ($r$) at a borda onde o raio do tubo ($R$) est (levando em considera o que a velocidade na borda zero), podemos obter la velocidade em um raio do cilindro ($v$) como fun o de o raio de curvatura ($r$):
Onde:
la taxa de fluxo máxima ($v_{max}$) no centro do fluxo.
Uma vez que la resistência hidráulica ($R_h$) igual a la condutância hidráulica ($G_h$) conforme a seguinte equa o:
e uma vez que la condutância hidráulica ($G_h$) expresso em termos de la viscosidade ($\eta$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) da seguinte forma:
podemos concluir que:
O fluxo definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equa o:
e o volume igual rea da se o la seção de tubo ($S$) multiplicada pela dist ncia percorrida o elemento de tubo ($\Delta s$):
Como a dist ncia percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde velocidade, ela representada por:
Assim, o fluxo uma densidade de fluxo ($j_s$), que calculado usando:
A defini o de o fluxo de volume ($J_V$) O elemento de volume ($\Delta V$) durante o tempo decorrido ($\Delta t$):
que, no limite de um intervalo de tempo infinitesimal, corresponde derivada de o volume ($V$) em rela o a o tempo ($t$):
Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):
podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:
para obter:
Exemplos
A solu o obtida para a altura e os par metros o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) nos mostra que la densidade de fluxo ($j_s$) igual a:
Podemos representar la densidade de fluxo ($j_s$) graficamente em termos dos fatores adicionais $j_s/j_{s0}$ e $x/x_0$ da seguinte maneira:
la densidade de fluxo ($j_s$) continua aumentando medida que nos aproximamos do canal, medida que la altura da coluna d'água no solo ($h$) diminui. Esse aumento necess rio para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, aument -la.
Quando um tubo preenchido com l quido de viscosidade ERROR:5422,0 exposto a la pressão na posição inicial ($p_i$) em o posição no início do tubo ($L_i$) e la pressão na posição final (e) ($p_e$) em o posição na extremidade do tubo ($L_e$), gera-se uma diferença de pressão ($\Delta p_s$) ao longo de o comprimento do tubo ($\Delta L$), resultando no perfil de la velocidade em um raio do cilindro ($v$):
Em fluxos com valores baixos de o número de Reynolds ($Re$), onde a viscosidade mais relevante do que a in rcia do l quido, o fluxo se desenvolve de forma laminar, ou seja, sem a presen a de turbul ncia.
No fluxo laminar, camadas adjacentes se movem e existe uma for a gerada pela viscosidade entre elas. A camada mais r pida arrasta sua vizinha mais lenta, enquanto a mais lenta restringe o avan o da mais r pida.
Portanto, a for a la força viscosa ($F_v$) gerada por ERROR:10119.1 sobre a outra uma fun o de ERROR:5556.1, ERROR:5436.1 e ERROR:5422.1, como mostrado na seguinte equa o:
ilustrado no seguinte diagrama:
O fluxo laminar ao redor de um cilindro pode ser representado como m ltiplas camadas cil ndricas deslizando sob a influ ncia das camadas adjacentes. Nesse caso, la força viscosa ($F_v$) com o comprimento do tubo ($\Delta L$), la viscosidade ($\eta$) e as vari veis la posição radial no cilindro ($r$) e la velocidade em um raio do cilindro ($v$) expresso como:
A camada na borda em ERROR:5417.1 permanece estacion ria devido ao efeito de borda e, atrav s de la viscosidade ($\eta$), retarda a camada adjacente que possui velocidade.
O centro a parte que se move em la taxa de fluxo máxima ($v_{max}$), arrastando a camada circundante. Por sua vez, essa camada arrasta a pr xima e assim por diante at atingir a camada em contato com a parede do cilindro, que est estacion ria.
Dessa forma, o sistema transfere energia do centro para a parede, gerando um perfil de velocidade representado por:
com:
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo atrav s da integra o de toda a superf cie, o que nos leva conhecida lei de Hagen-Poiseuille.
O resultado uma equa o que depende de ERROR:5417,0 elevado quarta pot ncia. No entanto, fundamental observar que este perfil de fluxo s v lido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ERROR:6673,1, a express o:
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre as leis que regem o fluxo da gua em recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Pesquisa experimental sobre o movimento de l quidos em tubos de di metros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
Durante um tempo decorrido ($\Delta t$), o fluido com uma velocidade média do fluido ($v$) se desloca um elemento de tubo ($\Delta s$). Se la seção ($S$) representa a quantidade de fluido que atravessa essa se o em o tempo decorrido ($\Delta t$), calculada como:
$\Delta V = S \Delta s = Sv \Delta t$
Esta equa o indica que o volume de fluido que flui atrav s da se o la seção ($S$) durante um tempo decorrido ($\Delta t$) igual ao produto da rea da se o e a dist ncia percorrida pelo fluido nesse tempo.
Isso facilita o c lculo de o elemento de volume ($\Delta V$), que o volume de fluido que flui pelo canal em um per odo espec fico de o tempo decorrido ($\Delta t$), correspondente a o fluxo de volume ($J_V$).
O crit rio chave para determinar se um meio laminar ou turbulento o chamado n mero de Reynolds, que compara a energia associada in rcia com aquela associada viscosidade. A primeira depende de la densidade ($\rho$), la velocidade média do fluido ($v$) e la dimensão típica do sistema ($R$), enquanto a segunda depende de la viscosidade ($\eta$), definindo-o como:
Quando la pressão na posição inicial ($p_i$) e la pressão na posição final (e) ($p_e$) s o conectados, uma la diferença de pressão ($\Delta p_s$) criada, a qual calculada usando a seguinte f rmula:
la diferença de pressão ($\Delta p_s$) representa a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.
Para descrever o fluxo, definido um sistema de coordenadas no qual o l quido flui de o posição no início do tubo ($L_i$) para o posição na extremidade do tubo ($L_e$), indicando que a press o em la pressão na posição inicial ($p_i$) maior do que em la pressão na posição final (e) ($p_e$). Este movimento depende de o comprimento do tubo ($\Delta L$), que calculado da seguinte forma:
La força viscosa ($F_v$) pode ser calculado a partir de os superfícies paralelas ($S$), la viscosidade ($\eta$), la diferença de velocidade entre superfícies ($\Delta v$) e la distância entre superfícies ($\Delta z$) utilizando o seguinte m todo:
No caso de um cilindro, a superf cie definida por ERROR:5430,0 e pelo per metro de cada um dos cilindros internos, que calculado multiplicando $2\pi$ por o raio de posição em um tubo ($r$). Com isso, la força de resistência no cilindro ($F_v$) calculada usando la viscosidade ($\eta$) e la variação de velocidade entre dois raios ($dv$) para a largura do cilindro o variação do raio em um tubo ($dr$), resultando em:
Ao resolver a equa o de fluxo com a condi o de contorno, obtemos la velocidade em um raio do cilindro ($v$) como uma fun o de o raio de curvatura ($r$), representada por uma par bola centrada em la taxa de fluxo máxima ($v_{max}$) e igual a zero em o raio do tubo ($R$):
O valor de la taxa de fluxo máxima ($v_{max}$) no centro de um cilindro depende de la viscosidade ($\eta$), o raio do tubo ($R$) e do gradiente criado por la diferença de pressão ($\Delta p_s$) e o comprimento do tubo ($\Delta L$), conforme representado abaixo:
O sinal negativo indica que o fluxo sempre ocorre na dire o oposta ao gradiente, ou seja, da rea de maior press o para a rea de menor press o.
O fluxo de volume ($J_V$) corresponde quantidade ERROR:9847,0 que flui pelo canal durante um tempo ($t$). Portanto, temos:
O fluxo de volume ($J_V$) pode ser calculado com a lei de Hagen-Poiseuille que com os par metros la viscosidade ($\eta$), la diferença de pressão ($\Delta p$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) :
Com o raio do tubo ($R$), la viscosidade ($\eta$) e o comprimento do tubo ($\Delta L$) temos que uma condutância hidráulica ($G_h$) :
Com a introdu o de la condutância hidráulica ($G_h$), podemos reescrever a equa o de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equa o:
No contexto da resist ncia el trica, existe o seu inverso, conhecido como a condut ncia el trica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) atrav s da express o:
Como la resistência hidráulica ($R_h$) igual ao inverso de la condutância hidráulica ($G_h$), ele pode ser calculado a partir da express o deste ltimo. Dessa forma, podemos identificar par metros relacionados geometria (o comprimento do tubo ($\Delta L$) e o raio do tubo ($R$)) e ao tipo de l quido (la viscosidade ($\eta$)), que podem ser denominados coletivamente como uma resistência hidráulica ($R_h$):
Darcy reescreve a equa o de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):
La superfície de um disco ($S$) de um raio do disco ($r$) calculada da seguinte forma:
Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) atrav s da seguinte f rmula:
O fator restante chamado la permeabilidade hidrodinâmica ($k$) e pode ser calculado usando o raio do tubo ($R$) com a seguinte f rmula:
ID:(369, 0)