Utilisateur:
L'écoulement de l'Eau
Storyboard 
Dans un sol saturé, il peut y avoir des situations où des variations de pression se produisent. Ces variations génèrent à leur tour un écoulement qui, dans ce cas, devrait se produire à l'intérieur des pores du sol. Étant donné que ces pores ont une taille de l'ordre des microns ou des dizaines de microns, l'écoulement a tendance à être laminaire en raison des faibles nombres de Reynolds.
ID:(369, 0)
L'écoulement de l'Eau
Storyboard
Dans un sol saturé, il peut y avoir des situations où des variations de pression se produisent. Ces variations génèrent à leur tour un écoulement qui, dans ce cas, devrait se produire à l'intérieur des pores du sol. Étant donné que ces pores ont une taille de l'ordre des microns ou des dizaines de microns, l'écoulement a tendance à être laminaire en raison des faibles nombres de Reynolds.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si nous examinons a conductance hydraulique ($G_h$), nous pouvons remarquer que le num rateur contient la section transversale du tube, repr sent e par $\pi R^2$. Ici, le rayon du tube ($R$) correspond une propri t du liquide, a viscosité ($\eta$) est li e la viscosit du fluide, et le longueur du tube ($\Delta L$) se r f re au gradient de pression g n r .
Ainsi, le facteur propre la g om trie des pores peut tre d fini comme a perméabilité hydrodynamique ($k$) en utilisant la formule suivante :
Si nous examinons le profil de ERROR:5449,0 pour un fluide dans un canal cylindrique, o a vitesse dans un rayon du cylindre ($v$) varie en fonction de ERROR:10120,0 selon l'expression suivante :
avec le rayon du tube ($R$) et a vitesse maximal ($v_{max}$). Nous pouvons calculer a vitesse maximal ($v_{max}$) en utilisant a viscosité ($\eta$), a différence de pression ($\Delta p$), et le longueur du tube ($\Delta L$) comme suit :
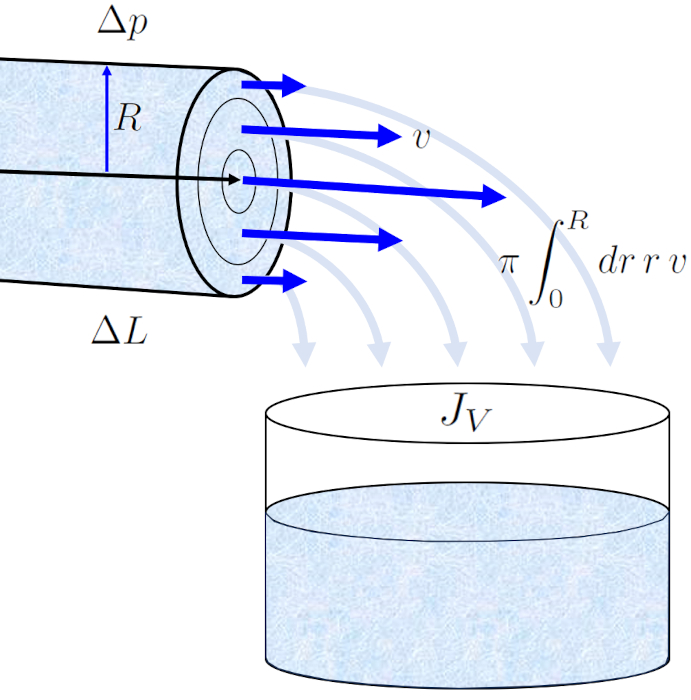
Si nous int grons la vitesse sur toute la section transversale du canal, nous obtenons le volumique flux ($J_V$), d fini comme l'int grale de $\pi r v(r)$ par rapport ERROR:10120,0 de $0$ ERROR:5417,0. Cette int grale peut tre simplifi e comme suit :
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
L'int gration donne la loi de Hagen-Poiseuille r sultante :
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
En fran ais, l' nonc donn serait le suivant :
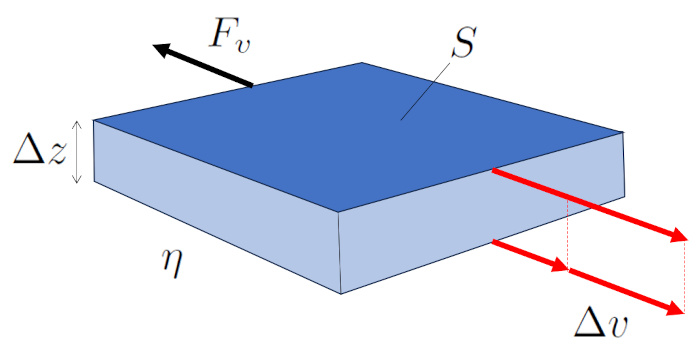
"Comme la force visqueuse est
et la surface du cylindre est
$S=2\pi R L$
o $R$ est le rayon et $L$ est la longueur du canal, la force visqueuse peut tre exprim e comme
o $\eta$ repr sente la viscosit et $dv/dr$ est le gradient de vitesse entre la paroi et l' coulement.
Quand une a différence de pression ($\Delta p_s$) agit sur une section avec une aire de $\pi R^2$, avec le rayon du tube ($R$) comme le rayon de courbure ($r$), elle g n re une force repr sent e par :
$\pi r^2 \Delta p$
Cette force pousse le liquide contre la r sistance visqueuse, donn e par :
En galant ces deux forces, nous obtenons :
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Ce qui nous conduit l' quation :
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si nous int grons cette quation d'une position d finie par le rayon de courbure ($r$) jusqu'au bord o se trouve le rayon du tube ($R$) (en tenant compte que la vitesse au bord est nulle), nous pouvons obtenir a vitesse dans un rayon du cylindre ($v$) en fonction de le rayon de courbure ($r$) :
O :
est a vitesse maximal ($v_{max}$) au centre de l' coulement.
Puisque a résistance hydraulique ($R_h$) est gal a conductance hydraulique ($G_h$) conform ment l' quation suivante :
et puisque a conductance hydraulique ($G_h$) est exprim en termes de a viscosité ($\eta$), le rayon du tube ($R$), et le longueur du tube ($\Delta L$) comme suit :
nous pouvons en conclure que :
Le flux est d fini comme le volume le élément de volume ($\Delta V$) divis par le temps le temps écoulé ($\Delta t$), ce qui est exprim dans l' quation suivante :
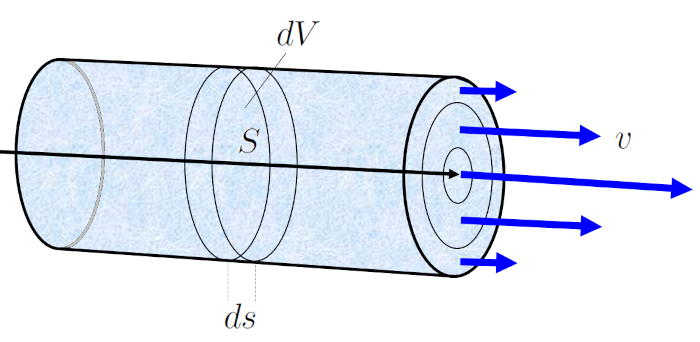
et le volume est gal la section transversale a section de tube ($S$) multipli e par la distance parcourue le élément tubulaire ($\Delta s$) :
tant donn que la distance parcourue le élément tubulaire ($\Delta s$) par unit de temps le temps écoulé ($\Delta t$) correspond la vitesse, elle est repr sent e par :
Ainsi, le flux est une densité de flux ($j_s$), qui est calcul l'aide de :
La d finition de le volumique flux ($J_V$) est le élément de volume ($\Delta V$) pendant le temps écoulé ($\Delta t$) :
qui, la limite d'un intervalle de temps infinit simal, correspond la d riv e de le volume ($V$) par rapport le temps ($t$) :
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Exemples
La solution obtenue pour la hauteur et les param tres le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) nous montre que a densité de flux ($j_s$) est gal :
Nous pouvons repr senter graphiquement a densité de flux ($j_s$) en fonction des facteurs additionnels $j_s/j_{s0}$ et $x/x_0$ comme suit :
a densité de flux ($j_s$) continue d'augmenter mesure que nous nous approchons du canal, tandis que a hauteur de la colonne d'eau au sol ($h$) diminue. Cette augmentation est n cessaire pour maintenir la vitesse d' coulement dans a densité de flux ($j_s$) ou, en alternative, pour l'augmenter.
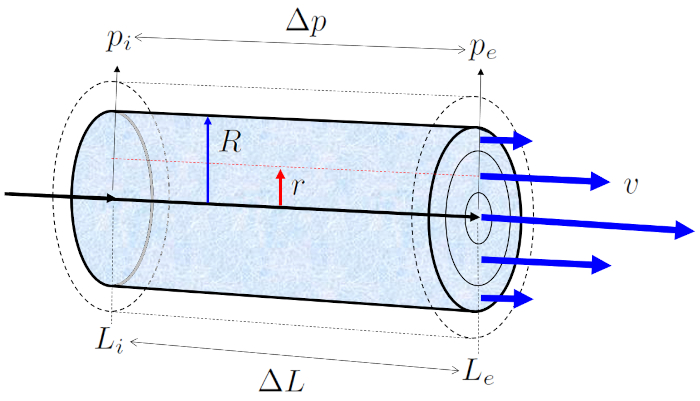
Lorsqu'un tube rempli de liquide d'une viscosit de ERROR:5422,0 est expos a pression en position initiale ($p_i$) en le positionner au début du tube ($L_i$) et a pression en position finale (e) ($p_e$) en le positionner au bout du tube ($L_e$), cela g n re une différence de pression ($\Delta p_s$) le long de le longueur du tube ($\Delta L$), ce qui donne le profil de a vitesse dans un rayon du cylindre ($v$) :
Dans les coulements avec de faibles valeurs de le le numéro de Reynold ($Re$), o la viscosit est plus significative que l'inertie du liquide, l' coulement se d veloppe de mani re lamin e, c'est- -dire sans la pr sence de turbulences.
Dans un coulement laminaire, des couches adjacentes se d placent et une force est g n r e par la viscosit entre elles. La couche la plus rapide entra ne sa voisine plus lente, tandis que la plus lente limite l'avancement de la plus rapide.
Par cons quent, la force a force visqueuse ($F_v$) g n r e par ERROR:10119.1 sur l'autre est une fonction de ERROR:5556.1, ERROR:5436.1 et ERROR:5422.1, comme indiqu dans l' quation suivante :
illustr e dans le sch ma suivant :
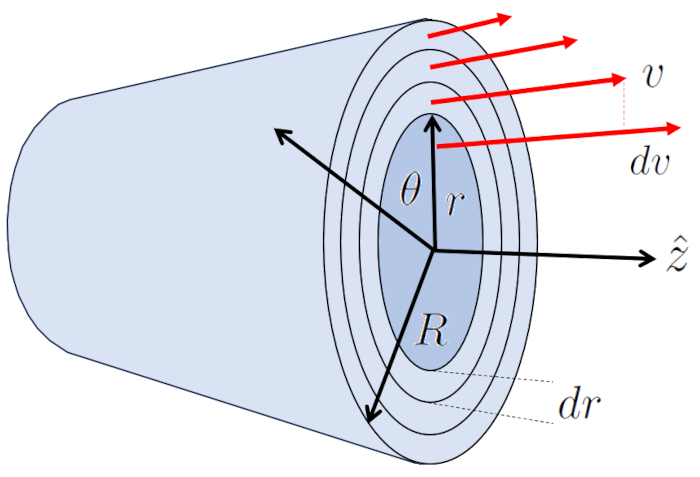
L' coulement laminaire autour d'un cylindre peut tre repr sent comme plusieurs couches cylindriques glissant sous l'influence des couches adjacentes. Dans ce cas, a force visqueuse ($F_v$) avec le longueur du tube ($\Delta L$), a viscosité ($\eta$) et les variables a position radiale dans le cylindre ($r$) et a vitesse dans un rayon du cylindre ($v$) est exprim e comme suit :
La couche la fronti re ERROR:5417.1 reste stationnaire en raison de l'effet de bord et, travers a viscosité ($\eta$), ralentit la couche adjacente qui a une vitesse.
Le centre est la partie qui se d place a vitesse maximal ($v_{max}$), entra nant la couche environnante. son tour, cette couche entra ne la suivante, et ainsi de suite jusqu' ce qu'elle atteigne la couche en contact avec la paroi du cylindre, qui est immobile.
Ainsi, le syst me transf re de l' nergie du centre vers la paroi, g n rant un profil de vitesse repr sent par :
avec :
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en int grant sur toute la surface, ce qui nous conduit la loi bien connue de Hagen-Poiseuille.
Le r sultat est une quation qui d pend de ERROR:5417,0 lev la quatri me puissance. Cependant, il est essentiel de noter que ce profil d' coulement n'est valable que dans le cas d'un coulement laminaire.
Ainsi, avec cela, on d duit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
Les articles originaux qui ont donn naissance cette loi avec un nom combin taient:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sur les lois r gissant l' coulement de l'eau dans des r cipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
Durant un temps écoulé ($\Delta t$), le fluide avec une vitesse moyenne du fluide ($v$) se d place de un élément tubulaire ($\Delta s$). Si a section ($S$) repr sente la quantit de fluide traversant cette section en le temps écoulé ($\Delta t$), elle se calcule comme suit :
$\Delta V = S \Delta s = Sv \Delta t$
Cette quation indique que le volume de fluide qui s' coule travers la section a section ($S$) durant un temps écoulé ($\Delta t$) est gal au produit de la surface de la section et de la distance parcourue par le fluide pendant ce temps.
Cela facilite le calcul de le élément de volume ($\Delta V$), qui est le volume de fluide s' coulant travers le canal sur une p riode sp cifique de le temps écoulé ($\Delta t$), correspondant le volumique flux ($J_V$).
Le crit re cl pour d terminer si un milieu est lamin ou turbulent est le num ro de Reynolds, qui compare l' nergie associ e l'inertie celle associ e la viscosit . La premi re d pend de a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a dimension typique du système ($R$), tandis que la seconde d pend de a viscosité ($\eta$), le d finissant ainsi :
Lorsque a pression en position initiale ($p_i$) et a pression en position finale (e) ($p_e$) sont connect s, une a différence de pression ($\Delta p_s$) est cr e, qui est calcul e l'aide de la formule suivante :
a différence de pression ($\Delta p_s$) repr sente la diff rence de pression qui fera couler le liquide de la colonne la plus haute vers la colonne la plus basse.
Pour d crire l' coulement, un syst me de coordonn es est d fini dans lequel le liquide s' coule de le positionner au début du tube ($L_i$) Le positionner au bout du tube ($L_e$), ce qui signifie que la pression en a pression en position initiale ($p_i$) est sup rieure celle en a pression en position finale (e) ($p_e$). Ce mouvement d pend de le longueur du tube ($\Delta L$), qui est calcul comme suit :
A force visqueuse ($F_v$) peut tre calcul partir de les surfaces parallèles ($S$), a viscosité ($\eta$), a différence de vitesse entre les surfaces ($\Delta v$) et a distance entre les surfaces ($\Delta z$) en utilisant la m thode suivante :
Dans le cas d'un cylindre, la surface est d finie par ERROR:5430,0, et par le p rim tre de chacun des cylindres internes, qui est calcul en multipliant $2\pi$ par le rayon de position dans un tube ($r$). Avec cela, a force de résistance en cylindre ($F_v$) est calcul e en utilisant a viscosité ($\eta$) et a variation de vitesse entre deux rayons ($dv$) pour la largeur du cylindre le variation de rayon dans un tube ($dr$), ce qui donne :
En r solvant l' quation de flux avec la condition aux limites, nous obtenons a vitesse dans un rayon du cylindre ($v$) comme une fonction de le rayon de courbure ($r$), repr sent e par une parabole centr e sur a vitesse maximal ($v_{max}$) et gale z ro en le rayon du tube ($R$) :
La valeur de a vitesse maximal ($v_{max}$) au centre d'un cylindre d pend de a viscosité ($\eta$), le rayon du tube ($R$) et du gradient cr par a différence de pression ($\Delta p_s$) et le longueur du tube ($\Delta L$), comme repr sent ci-dessous :
Le signe n gatif indique que le flux s'effectue toujours dans la direction oppos e au gradient, c'est- -dire, de la zone de plus haute pression vers la zone de plus basse pression.
Le volumique flux ($J_V$) correspond la quantit ERROR:9847,0 qui s' coule travers le canal pendant un temps ($t$). Par cons quent, nous avons :
Le volumique flux ($J_V$) peut tre calcul avec la loi de Hagen-Poiseuille qui avec les param tres a viscosité ($\eta$), a différence de pression ($\Delta p$), le rayon du tube ($R$) et le longueur du tube ($\Delta L$) estxa0:
Avec le rayon du tube ($R$), a viscosité ($\eta$) et le longueur du tube ($\Delta L$) nous avons que une conductance hydraulique ($G_h$) vautxa0:
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons r crire l' quation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) l'aide de l' quation suivante :
Dans le contexte de la r sistance lectrique, son inverse existe, connu sous le nom de conductance lectrique. De mani re similaire, ce qui serait a conductance hydraulique ($G_h$) peut tre d fini en termes de a résistance hydraulique ($R_h$) travers l'expression :
Puisque a résistance hydraulique ($R_h$) est gal l'inverse de a conductance hydraulique ($G_h$), il peut tre calcul partir de l'expression de ce dernier. De cette mani re, nous pouvons identifier des param tres li s la g om trie (le longueur du tube ($\Delta L$) et le rayon du tube ($R$)) et au type de liquide (a viscosité ($\eta$)), qui peuvent tre collectivement d sign s sous le nom de une résistance hydraulique ($R_h$) :
Darcy r crit l' quation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit gal a résistance hydraulique ($R_h$) fois le volumique flux ($J_V$)xa0:
A section ($S$) de un rayon du disque ($r$) est calcul e comme suit :
Une densité de flux ($j_s$) peut tre exprim en termes de le volumique flux ($J_V$) l'aide de a coupe ou surface ($S$) par la formule suivante :
Le facteur restant est appel a perméabilité hydrodynamique ($k$) et peut tre calcul en utilisant le rayon du tube ($R$) avec la formule suivante :
ID:(369, 0)
