Wärmetransport
Storyboard 
Die Feuchtigkeit im Boden hängt von seiner Temperatur ab, daher ist es wichtig, diese Verteilung zu berechnen. Diese Beziehung wird durch den Wärmeaustausch mit der Bodenoberfläche bestimmt.
ID:(2054, 0)
Wärmetransport
Modell 
Die Feuchtigkeit im Boden hängt von seiner Temperatur ab, daher ist es wichtig, diese Verteilung zu berechnen. Diese Beziehung wird durch den Wärmeaustausch mit der Bodenoberfläche bestimmt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Mit die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und die Temperaturdifferenz ($\Delta T$) erhalten wir
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
die mit die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
und mit die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
als
$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$
definieren k nnen wir einen kombinierten Koeffizienten als
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 3486)
Mit die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und die Temperaturdifferenz ($\Delta T$) erhalten wir
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
die mit die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
und mit die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
und
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
als
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
resultiert in
| $ q = k \Delta T $ |
(ID 7716)
(ID 15116)
Mit die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturdifferenz ($\Delta T$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) erhalten wir
| $ q = k \Delta T $ |
was mit der Interner Übertragungskoeffizient ($\alpha_i$) und die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$)
| $ q = \alpha_i \Delta T_i $ |
ergibt
$k\Delta T = \alpha_i \Delta T_i$
und mit die Innentemperatur ($T_i$) und die Innenoberflächentemperatur ($T_{is}$) und
| $ \Delta T_i = T_i - T_{is} $ |
resultiert in
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
(ID 15121)
Mit die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$), die Temperaturdifferenz ($\Delta T$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) erhalten wir
| $ q = k \Delta T $ |
was, mit der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$)
| $ q = \alpha_e \Delta T_e $ |
zu
$k\Delta T = \alpha_e \Delta T_e$
und mit die Außentemperatur ($T_e$) und die Äußere Oberflächentemperatur ($T_{es}$) und
| $ \Delta T_e = T_{es} - T_e $ |
zu
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
f hrt.
(ID 15122)
Beispiele
(ID 15207)
Im Fall eines Festk rpers und hnlich f r eine Fl ssigkeit k nnen wir das System als eine Struktur von Atomen beschreiben, die durch etwas verbunden sind, das sich wie eine Feder verh lt. Wenn beide Enden Temperaturen von eine Temperaturunterschied im Leiter ($\Delta T_0$) haben, wobei die Innenoberflächentemperatur ($T_{is}$) und die Äußere Oberflächentemperatur ($T_{es}$) sind:
| $ \Delta T_0 = T_{is} - T_{es} $ |
Der Temperaturunterschied bedeutet, dass die Atome an den Enden unterschiedlich schwingen; Atome in der Zone mit hoher Temperatur haben eine gr ere Amplitude in ihren Schwingungen im Vergleich zu den Atomen in der Zone mit niedriger Temperatur.

Diese Differenz f hrt jedoch allm hlich dazu, dass die gesamte Kette so schwingt, dass die Amplitude am Wegesrand von den h chsten Werten, wo die Temperatur ebenfalls h her ist, bis zu den niedrigsten Werten in der Zone mit niedrigerer Temperatur variiert.
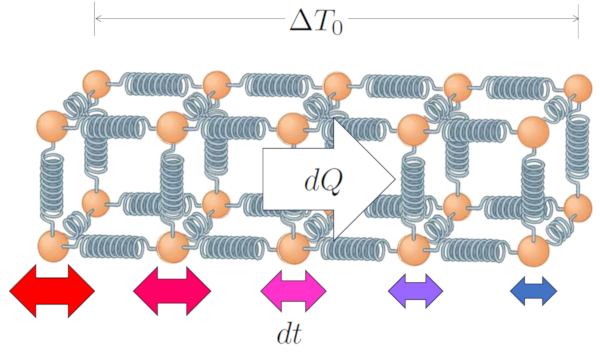
Auf diese Weise f hrt die Temperaturunterschied im Leiter ($\Delta T_0$) zu eine Wärme transportiert ($dQ$) in eine Zeitvariation ($dt$).
(ID 15234)
Einer der Schl sselfaktoren, der bestimmt, wie viel W rme durch einen Feststoff oder eine Fl ssigkeit geleitet werden kann, ist sein Querschnitt, das hei t, die Anzahl der verf gbaren Atomketten. Je mehr dieser Ketten wir haben, desto gr er ist unsere W rmetransportkapazit t.
Jedoch kann die L nge dieser Ketten kontraproduktiv sein. Wenn die Federkette l nger wird, nimmt unsere F higkeit zur W rme bertragung ab, da mehr Atome ihre Schwingungsamplituden anpassen m ssen.
Wenn wir dies mit die Abschnitt ($S$) und der Leitungslänge ($L$) darstellen, nimmt das Diagramm folgende Form an:

Schlie lich erkl rt die F higkeit des Mediums und des Materials zur W rme bertragung, die durch die Koeffizienten der Interner Übertragungskoeffizient ($\alpha_i$) und der Externer Transmissionskoeffizient ($\alpha_e$) und die Wärmeleitfähigkeit ($\lambda$) beschrieben wird, wie die W rme in Reaktion auf die Temperaturdifferenz ($\Delta T$) bertragen wird, das durch die Differenz zwischen die Innentemperatur ($T_i$) und die Außentemperatur ($T_e$) erzeugt wird:

Dies wird wie folgt berechnet:
| $ \Delta T = T_i - T_e $ |
(ID 15235)
Die W rmeleitung wurde erstmals von Jean Baptiste Joseph Fourier [1] modelliert, der festlegte, dass die Wärmestromrate ($q$), definiert durch die Wärme transportiert ($dQ$), die Zeitvariation ($dt$) und die Abschnitt ($S$), durch die folgende Gleichung ausgedr ckt wird:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Diese Theorie steht auch in Beziehung zu die Abschnitt ($S$), der Leitungslänge ($L$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Wärmeleitfähigkeit ($\lambda$), wie in der folgenden Gleichung dargestellt:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
und wird durch das folgende Diagramm veranschaulicht:
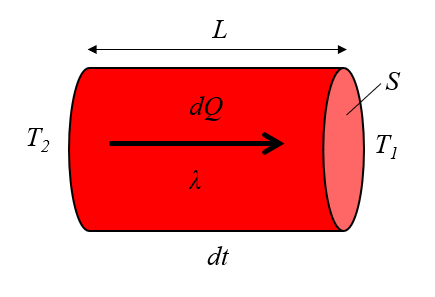
![]() [1] "Th orie Analytique de la Chaleur" (Die analytische Theorie der W rme), Jean Baptiste Joseph Fourier, 1822.
[1] "Th orie Analytique de la Chaleur" (Die analytische Theorie der W rme), Jean Baptiste Joseph Fourier, 1822.
(ID 15236)
Der Haupttreiber f r den W rme bergang von einem Medium auf einen Leiter ist der Temperaturunterschied. In dem Medium die Innentemperatur ($T_i$) haben die Teilchen mehr Energie, und wenn sie mit denen im Leiter bei eine Innenoberflächentemperatur ($T_{is}$) kollidieren, neigen sie dazu, die Energie des Letzteren zu erh hen. Diese Interaktion kann wie folgt dargestellt werden:
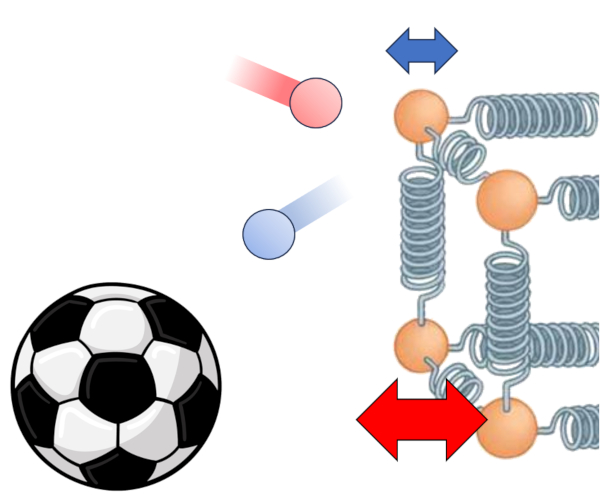
Neben der Temperatur selbst h ngt der W rmefluss von die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) ab:
| $ \Delta T_i = T_i - T_{is} $ |
Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erh ht werden kann, was von die Abschnitt ($S$) abh ngt. Schlie lich m ssen wir auch die Eigenschaften der Oberfl che ber cksichtigen, die durch der Interner Übertragungskoeffizient ($\alpha_i$) beschrieben werden. Dies entspricht dem Verh ltnis zwischen bertragener W rme, Oberfl che, Temperaturunterschied und verstrichener Zeit:
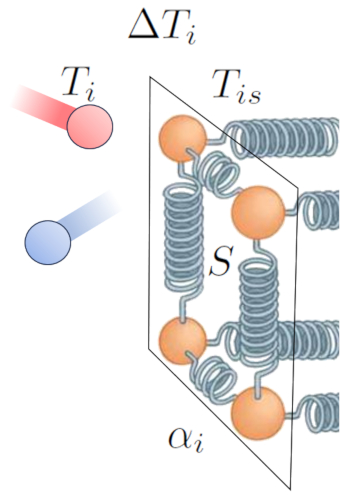
(ID 15237)
Auf diese Weise etablieren wir eine Beziehung, die es uns erm glicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$) zu berechnen:
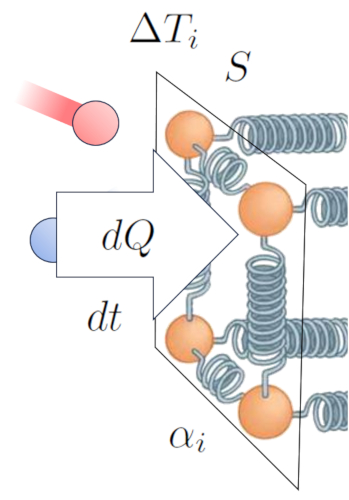
Dies kann mathematisch wie folgt ausgedr ckt werden:
| $ q = \alpha_i \Delta T_i $ |
(ID 15238)
Der Haupttreiber f r den W rme bergang von einem Leiter zu einem Medium ist der Temperaturunterschied. Wenn die Äußere Oberflächentemperatur ($T_{es}$), haben die Teilchen mehr Energie und schwingen mit einer gr eren Amplitude, wenn sie mit den Atomen und Molek len des Mediums bei eine Außentemperatur ($T_e$) interagieren. Dies f hrt dazu, dass die Energie dieser letzten erh ht wird. Diese Interaktion kann wie folgt dargestellt werden:

Neben der Temperatur h ngt der W rmefluss von die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) ab.
| $ \Delta T_e = T_{es} - T_e $ |
Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erh ht werden kann, was von die Abschnitt ($S$) abh ngt. Abschlie end m ssen wir die Oberfl cheneigenschaften ber cksichtigen, die durch der Externer Transmissionskoeffizient ($\alpha_e$) repr sentiert werden. Dies entspricht dem Verh ltnis zwischen bertragener W rme, Oberfl che, Temperaturunterschied und verstrichener Zeit:

(ID 15239)
Auf diese Weise etablieren wir eine Beziehung, die es uns erm glicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und der Externer Transmissionskoeffizient ($\alpha_e$) zu berechnen:
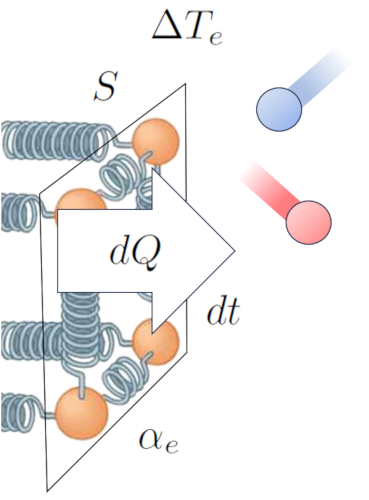
Dies kann mathematisch wie folgt ausgedr ckt werden:
| $ q = \alpha_e \Delta T_e $ |
(ID 15240)
W rme bertragungs- und Leitungsmodelle legen nahe, dass es m glich ist, eine Beziehung zu entwickeln, die alle drei Mechanismen zusammenfasst. Diese Gleichung sollte die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Temperaturdifferenz ($\Delta T$), die Abschnitt ($S$) und der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) ber cksichtigen:

Mathematisch kann dies wie folgt ausgedr ckt werden:
| $ q = k \Delta T $ |
(ID 15241)
Einer der Effekte der W rme bertragung von einem Leiter auf ein externes Medium ist die Erw rmung des Mediums nahe der Schnittstelle, was eine Interferenzzone in der bertragung schafft. Dies verringert die Effizienz der bertragung und f hrt dazu, dass eine isolierende Schicht entsteht, die den Energiefluss reduziert.
Dieser Effekt kann sich jedoch in Anwesenheit von Wind ndern. Der Wind kann die Schicht aus hochtemperierten Atomen und Molek len entfernen, wodurch die Effizienz der W rme bertragung verbessert wird. Dies deutet darauf hin, dass der Durchgangskoeffizient ($\alpha$) von die Mittlere Geschwindigkeit ($v_m$) beeinflusst wird [1,2]:
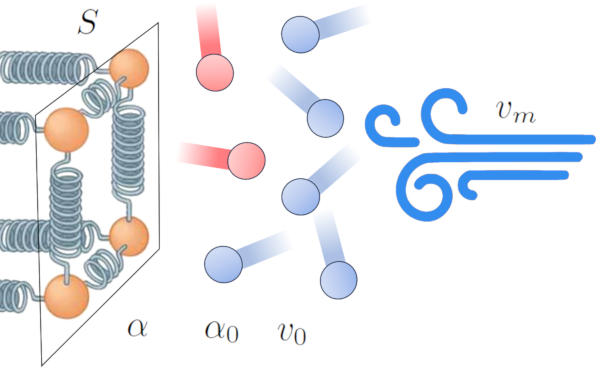
In diesem Zusammenhang modellieren wir die Beziehung basierend auf ERROR:9844,0 und einem Referenzfaktor von der Medienreferenzgeschwindigkeit ($v_0$).
Die mathematische Beziehung, die dieses Ph nomen f r ein Gas mit der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$), die Mittlere Geschwindigkeit ($v_m$), der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$) beschreibt, ist:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Und f r eine Fl ssigkeit mit der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$), die Mittlere Geschwindigkeit ($v_m$), der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Dies zeigt, wie der Wind die Effizienz der W rme bertragung zwischen einem Leiter und einem externen Medium erheblich beeinflussen kann.![]() [1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung", Ludwig Prandtl, 1904
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung", Ludwig Prandtl, 1904![]() [2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge", Wilhelm Nusselt, 1910
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge", Wilhelm Nusselt, 1910
(ID 3620)
(ID 15229)
ID:(2054, 0)
