User:
Heat transport
Storyboard 
The moisture content in the soil is dependent on its temperature, making it essential to calculate this distribution. This relationship is determined by the heat flux exchanged with the soil's surface.
ID:(2054, 0)
Heat transport mechanism
Image
In the case of a solid, and similarly for a liquid, we can describe the system as a structure of atoms held together by something that behaves like a spring. When both ends have temperatures of ERROR:10165.1, with the inner surface temperature ($T_{is}$) and the outer surface temperature ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
The temperature difference implies that the atoms at the ends oscillate differently; atoms in the high-temperature zone will have a greater amplitude in their oscillations compared to the atoms in the low-temperature zone.
However, this difference will gradually lead to the entire chain oscillating in such a way that, in the end, the amplitude will vary along the path, from the highest values where the temperature is also higher, to the lowest values in the lower-temperature zone.
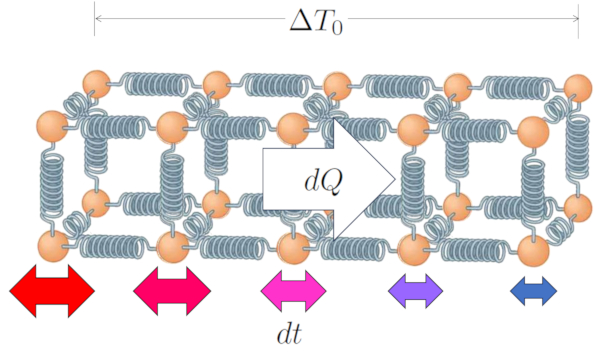
In this way, the temperature difference in the conductor ($\Delta T_0$) leads to ERROR:10159.1 in ERROR:10160.1.
ID:(15234, 0)
Geometry and material dependence
Note
One of the key factors determining how much heat can be conducted through a solid or liquid is its cross-sectional area, which refers to the quantity of atom chains available. The more of these chains we have, the greater our heat transport capacity.
However, the length of these chains can be counterproductive. As the spring chain becomes longer, our ability to transmit heat decreases, as more atoms must adjust their oscillation amplitudes.
If we represent this with the section ($S$) and the conductor length ($L$), the diagram takes the following form:
Finally, the ability of the medium and material to transport heat, described by coefficients the internal transmission coefficient ($\alpha_i$) and the external transmission coefficient ($\alpha_e$), and the thermal conductivity ($\lambda$), explains how heat moves in response to the temperature difference ($\Delta T$) created by the difference between the indoor temperature ($T_i$) and the outdoor temperature ($T_e$):
This is calculated as:
| $ \Delta T = T_i - T_e $ |
ID:(15235, 0)
Heat conduction
Quote
Heat conduction was first modeled by Jean Baptiste Joseph Fourier [1], who established that the heat flow rate ($q$), defined using the heat transported ($dQ$), the time variation ($dt$), and the section ($S$), is expressed by:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
This theory is also related to the section ($S$), the conductor length ($L$), the temperature difference in the conductor ($\Delta T_0$), and the thermal conductivity ($\lambda$), as shown in:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
and is illustrated with the following diagram:
[1] "Théorie Analytique de la Chaleur" (The Analytical Theory of Heat), Jean Baptiste Joseph Fourier, 1822.
ID:(15236, 0)
Dependence of heat transfer on geometry to the conductor
Exercise
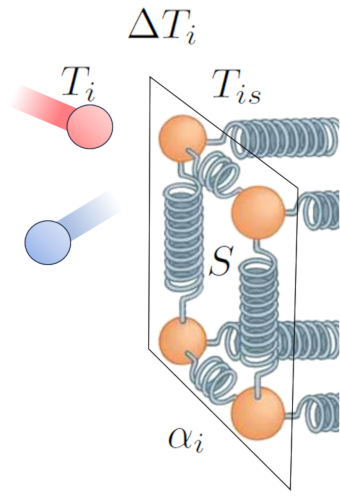
The primary driver of heat transfer from a medium to a conductor is the difference in temperature. In the medium the indoor temperature ($T_i$), particles have more energy, and when they collide with those in the conductor at ERROR:5212.1, they tend to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature itself, the heat flow depends on the temperature difference at internal interface ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Another key factor is the number of atoms whose oscillation amplitude can be increased, which depends on the section ($S$). Lastly, we must consider surface properties, described by the internal transmission coefficient ($\alpha_i$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
ID:(15237, 0)
Calculation of heat transmission to the conductor
Equation
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
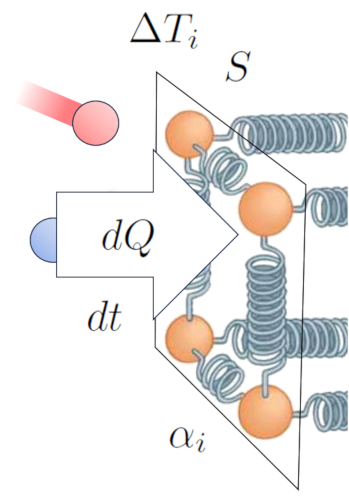
This can be expressed mathematically as follows:
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Dependence of heat transfer on geometry from the conductor
Script
The primary driver of heat transfer from a conductor to a medium is the temperature difference. When the outer surface temperature ($T_{es}$), particles have more energy and oscillate with a greater amplitude when interacting with the atoms and molecules of the medium at ERROR:5207.1. This tends to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature, the heat flow depends on the temperature difference at external interface ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Another key factor is the number of atoms that can have their oscillation amplitude increased, which depends on the section ($S$). Finally, we must consider surface properties, represented by the external transmission coefficient ($\alpha_e$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
ID:(15239, 0)
Heat transfer from the conductor
Variable
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
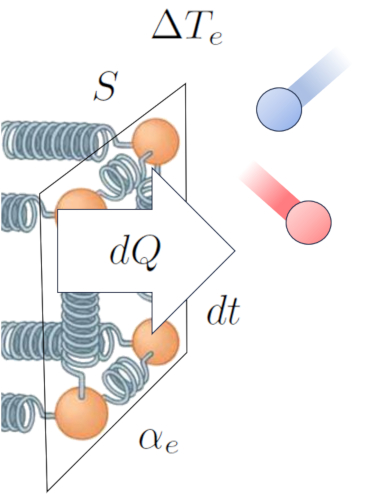
This can be expressed mathematically as follows:
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Total heat transport by a conductor
Audio
Heat transfer and conduction models suggest that it is possible to develop a relationship that incorporates all three mechanisms together. This equation should take into account the heat transported ($dQ$), the time variation ($dt$), the temperature difference ($\Delta T$), the section ($S$), and the total transport coefficient (multiple medium, two interfaces) ($k$):
Mathematically, this can be expressed as follows:
| $ q = k \Delta T $ |
ID:(15241, 0)
Dependence of the transfer coefficient on the velocity of the medium
Video
One of the effects of heat transfer from a conductor to an external medium is the heating of the medium near the interface, creating an interference zone in the transmission. This decreases the efficiency of the transfer and tends to form an insulating layer that reduces the flow of energy.
However, this effect can change in the presence of wind. The wind can remove the layer of high-temperature atoms and molecules, enhancing the efficiency of heat transfer. This suggests that the transmission coefficient ($\alpha$) is influenced by the mean speed ($v_m$) [1,2]:
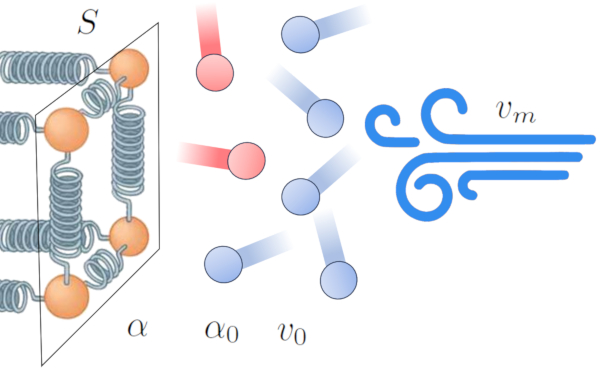
In this context, we model the relationship based on ERROR:9844,0 and a reference factor of the media reference speed ($v_0$).
The mathematical relationship that describes this phenomenon for a gas with the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$), the mean speed ($v_m$), the transmission coefficient in gases, independent of speed ($\alpha_{g0}$), and the transmission coefficient gas velocity factor ($v_{g0}$) is:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
And for a liquid with the transmission coefficient dependent on the speed ($\alpha_{wv}$), the mean speed ($v_m$), the transmission coefficient Independent of the speed ($\alpha_{w0}$), and the factor velocidad del coefiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
This illustrates how wind can significantly influence the efficiency of heat transfer between a conductor and an external medium.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung" (On Fluid Movement with Very Little Friction), Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge" (The Dependence of the Heat Transfer Coefficient on the Length of the Pipe), Wilhelm Nusselt, 1910
ID:(3620, 0)
Heat transport
Description
The moisture content in the soil is dependent on its temperature, making it essential to calculate this distribution. This relationship is determined by the heat flux exchanged with the soil's surface.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
With the temperature difference at internal interface ($\Delta T_i$), the temperature difference in the conductor ($\Delta T_0$), the temperature difference at external interface ($\Delta T_e$), and the temperature difference ($\Delta T$), we obtain
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
which can be rewritten with the heat transported ($dQ$), the time variation ($dt$), the section ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
and with the thermal conductivity ($\lambda$) and the conductor length ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
as
$\Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \displaystyle\frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right)$
so we can define a combined coefficient as
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 3486)
With the temperature difference at internal interface ($\Delta T_i$), the temperature difference in the conductor ($\Delta T_0$), the temperature difference at external interface ($\Delta T_e$), and the temperature difference ($\Delta T$), we obtain
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
which can be rewritten with the heat transported ($dQ$), the time variation ($dt$), the section ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
and with the thermal conductivity ($\lambda$) and the conductor length ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
and
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
as
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
resulting in
| $ q = k \Delta T $ |
(ID 7716)
(ID 15116)
With the heat transported ($dQ$), the time variation ($dt$), the section ($S$), the temperature difference ($\Delta T$), and the total transport coefficient (multiple medium, two interfaces) ($k$), we have
| $ q = k \Delta T $ |
which, with the internal transmission coefficient ($\alpha_i$) and the temperature difference at internal interface ($\Delta T_i$)
| $ q = \alpha_i \Delta T_i $ |
results in
$k\Delta T = \alpha_i \Delta T_i$
and with the indoor temperature ($T_i$) and the inner surface temperature ($T_{is}$) and
| $ \Delta T_i = T_i - T_{is} $ |
results in
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
(ID 15121)
With the heat transported ($dQ$), the time variation ($dt$), the section ($S$), the temperature difference ($\Delta T$), and the total transport coefficient (multiple medium, two interfaces) ($k$), we obtain
| $ q = k \Delta T $ |
which, with the external transmission coefficient ($\alpha_e$) and the temperature difference at external interface ($\Delta T_e$)
| $ q = \alpha_e \Delta T_e $ |
results in
$k\Delta T = \alpha_e \Delta T_e$
and with the outdoor temperature ($T_e$) and the outer surface temperature ($T_{es}$) and
| $ \Delta T_e = T_{es} - T_e $ |
results in
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
(ID 15122)
Examples
(ID 15207)
In the case of a solid, and similarly for a liquid, we can describe the system as a structure of atoms held together by something that behaves like a spring. When both ends have temperatures of ERROR:10165.1, with the inner surface temperature ($T_{is}$) and the outer surface temperature ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
The temperature difference implies that the atoms at the ends oscillate differently; atoms in the high-temperature zone will have a greater amplitude in their oscillations compared to the atoms in the low-temperature zone.
However, this difference will gradually lead to the entire chain oscillating in such a way that, in the end, the amplitude will vary along the path, from the highest values where the temperature is also higher, to the lowest values in the lower-temperature zone.
In this way, the temperature difference in the conductor ($\Delta T_0$) leads to ERROR:10159.1 in ERROR:10160.1.
(ID 15234)
One of the key factors determining how much heat can be conducted through a solid or liquid is its cross-sectional area, which refers to the quantity of atom chains available. The more of these chains we have, the greater our heat transport capacity.
However, the length of these chains can be counterproductive. As the spring chain becomes longer, our ability to transmit heat decreases, as more atoms must adjust their oscillation amplitudes.
If we represent this with the section ($S$) and the conductor length ($L$), the diagram takes the following form:
Finally, the ability of the medium and material to transport heat, described by coefficients the internal transmission coefficient ($\alpha_i$) and the external transmission coefficient ($\alpha_e$), and the thermal conductivity ($\lambda$), explains how heat moves in response to the temperature difference ($\Delta T$) created by the difference between the indoor temperature ($T_i$) and the outdoor temperature ($T_e$):
This is calculated as:
| $ \Delta T = T_i - T_e $ |
(ID 15235)
Heat conduction was first modeled by Jean Baptiste Joseph Fourier [1], who established that the heat flow rate ($q$), defined using the heat transported ($dQ$), the time variation ($dt$), and the section ($S$), is expressed by:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
This theory is also related to the section ($S$), the conductor length ($L$), the temperature difference in the conductor ($\Delta T_0$), and the thermal conductivity ($\lambda$), as shown in:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
and is illustrated with the following diagram:
[1] "Th orie Analytique de la Chaleur" (The Analytical Theory of Heat), Jean Baptiste Joseph Fourier, 1822.
(ID 15236)
The primary driver of heat transfer from a medium to a conductor is the difference in temperature. In the medium the indoor temperature ($T_i$), particles have more energy, and when they collide with those in the conductor at ERROR:5212.1, they tend to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature itself, the heat flow depends on the temperature difference at internal interface ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Another key factor is the number of atoms whose oscillation amplitude can be increased, which depends on the section ($S$). Lastly, we must consider surface properties, described by the internal transmission coefficient ($\alpha_i$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
(ID 15237)
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
This can be expressed mathematically as follows:
| $ q = \alpha_i \Delta T_i $ |
(ID 15238)
The primary driver of heat transfer from a conductor to a medium is the temperature difference. When the outer surface temperature ($T_{es}$), particles have more energy and oscillate with a greater amplitude when interacting with the atoms and molecules of the medium at ERROR:5207.1. This tends to increase the energy of the latter. This interaction can be represented as follows:
Beyond temperature, the heat flow depends on the temperature difference at external interface ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Another key factor is the number of atoms that can have their oscillation amplitude increased, which depends on the section ($S$). Finally, we must consider surface properties, represented by the external transmission coefficient ($\alpha_e$), which corresponds to the relationship between transmitted heat, surface area, temperature difference, and elapsed time:
(ID 15239)
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
This can be expressed mathematically as follows:
| $ q = \alpha_e \Delta T_e $ |
(ID 15240)
Heat transfer and conduction models suggest that it is possible to develop a relationship that incorporates all three mechanisms together. This equation should take into account the heat transported ($dQ$), the time variation ($dt$), the temperature difference ($\Delta T$), the section ($S$), and the total transport coefficient (multiple medium, two interfaces) ($k$):
Mathematically, this can be expressed as follows:
| $ q = k \Delta T $ |
(ID 15241)
One of the effects of heat transfer from a conductor to an external medium is the heating of the medium near the interface, creating an interference zone in the transmission. This decreases the efficiency of the transfer and tends to form an insulating layer that reduces the flow of energy.
However, this effect can change in the presence of wind. The wind can remove the layer of high-temperature atoms and molecules, enhancing the efficiency of heat transfer. This suggests that the transmission coefficient ($\alpha$) is influenced by the mean speed ($v_m$) [1,2]:
In this context, we model the relationship based on ERROR:9844,0 and a reference factor of the media reference speed ($v_0$).
The mathematical relationship that describes this phenomenon for a gas with the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$), the mean speed ($v_m$), the transmission coefficient in gases, independent of speed ($\alpha_{g0}$), and the transmission coefficient gas velocity factor ($v_{g0}$) is:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
And for a liquid with the transmission coefficient dependent on the speed ($\alpha_{wv}$), the mean speed ($v_m$), the transmission coefficient Independent of the speed ($\alpha_{w0}$), and the factor velocidad del coefiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
This illustrates how wind can significantly influence the efficiency of heat transfer between a conductor and an external medium.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (On Fluid Movement with Very Little Friction), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (The Dependence of the Heat Transfer Coefficient on the Length of the Pipe), Wilhelm Nusselt, 1910
(ID 3620)
(ID 15229)
In the case of a solid, and similarly for a liquid, we can describe the system as a structure of atoms held together by something that behaves like a spring. When both ends have temperatures of ERROR:10165.1, with the inner surface temperature ($T_{is}$) and the outer surface temperature ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
(ID 15120)
The temperature difference ($\Delta T$) is calculated by subtracting the outdoor temperature ($T_e$) and the indoor temperature ($T_i$), which is expressed as:
| $ \Delta T = T_i - T_e $ |
(ID 15116)
The heat flux ($q$) is a function of the thermal conductivity ($\lambda$), the conductor length ($L$) and the temperature difference in the conductor ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
(ID 7712)
The temperature difference at internal interface ($\Delta T_i$) is calculated by subtracting the inner surface temperature ($T_{is}$) from the indoor temperature ($T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
(ID 15117)
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) based on the temperature difference at internal interface ($\Delta T_i$), and the internal transmission coefficient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
(ID 15113)
The temperature difference at external interface ($\Delta T_e$) is calculated by subtracting the outer surface temperature ($T_{es}$) from the outdoor temperature ($T_e$):
| $ \Delta T_e = T_{es} - T_e $ |
(ID 15118)
In this manner, we establish a relationship that enables us to calculate the heat flow rate ($q$) based on the temperature difference at external interface ($\Delta T_e$), and the external transmission coefficient ($\alpha_e$):
| $ q = \alpha_e \Delta T_e $ |
(ID 15114)
In this way, we establish a relationship that allows us to calculate the heat flow rate ($q$) as a function of the total transport coefficient (multiple medium, two interfaces) ($k$), and the temperature difference ($\Delta T$):
| $ q = k \Delta T $ |
(ID 7716)
In the process of heat transfer, the temperature gradually decreases from the system with the highest temperature (internal) to the one with the lowest temperature (external). In this process, it first decreases from the internal average temperature to the temperature difference at internal interface ($\Delta T_i$), then to the temperature difference in the conductor ($\Delta T_0$), and finally to the temperature difference at external interface ($\Delta T_e$). The sum of these three variations equals the total drop, that is, the temperature difference ($\Delta T$), as shown below:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
(ID 15115)
The value of the coefficient of total transportation ($k$) in the transport equation is determined using the external transmission coefficient ($\alpha_e$), the internal transmission coefficient ($\alpha_i$), the thermal conductivity ($\lambda$), and the conductor length ($L$) as follows:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 3486)
The inner surface temperature ($T_{is}$) is not equal to the temperature of the medium itself, which is the indoor temperature ($T_i$). This temperature can be calculated from the temperature difference ($\Delta T$), the total transport coefficient (multiple medium, two interfaces) ($k$), and the internal transmission coefficient ($\alpha_i$) using the following formula:
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
(ID 15121)
The outer surface temperature ($T_{es}$) is not equal to the temperature of the medium, which is the outdoor temperature ($T_e$). This temperature can be calculated from the temperature difference ($\Delta T$), the total transport coefficient (multiple medium, two interfaces) ($k$), and the external transmission coefficient ($\alpha_e$) using the following formula:
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
(ID 15122)
The value of the coefficient of total transportation ($k$) in the transport equation is determined using the external transmission coefficient ($\alpha_e$), the thermal conductivity ($\lambda$) and the conductor length ($L$) as follows:
| $ \displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 3619)
The value of the heat flow rate ($q$) in the transport equation is determined using the internal transmission coefficient ($\alpha_i$), the external transmission coefficient ($\alpha_e$), the thermal conductivity element i ($\lambda_i$) and the element length i ($L_i$) as follows:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
(ID 7730)
In the event that a medium moves with a constant value of ERROR:5250.1 and the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$) is equal to
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
where the transmission coefficient in gases, independent of speed ($\alpha_{g0}$) represents the scenario where the medium does not move, and the transmission coefficient gas velocity factor ($v_{g0}$) is the reference velocity.
The thermal transfer constant for the material in the case of a stationary gas is equal to $5.6 J/m^2sK$, while the reference velocity is $1.41 m/s$.
(ID 7715)
If a medium is moving with a constant of the transmission coefficient dependent on the speed ($\alpha_{wv}$), and the mean speed ($v_m$) is equal to
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
where the transmission coefficient Independent of the speed ($\alpha_{w0}$) represents the case where the medium is not moving, and the factor velocidad del coefiente de transmisión ($v_{w0}$) is the reference velocity.
The thermal transfer constant of the material for the case of a stationary liquid is equal to $340 J/m^2sK$, while the reference velocity is $0.0278 m/s$.
(ID 7714)
Modeling thermal conductivity in a porous medium like soil is a challenging task. In this study, a wide range of samples was analyzed, and a numerical model was developed to predict the thermal conductivity in dry soil ($\lambda_b$) based on soil textures [1].
The relationship of the thermal conductivity in dry soil ($\lambda_b$) was determined in terms of the thermal conductivity in sand ($\lambda_a$), the thermal conductivity in silt ($\lambda_i$), the thermal conductivity in clay ($\lambda_c$), and the mass fraction of sand in the sample ($g_a$), the mass fraction of silt in the sample ($g_i$), the mass fraction of clay in the sample ($g_c$), using the following formula:
| $ \lambda_b = \lambda_a g_a + \lambda_i g_i + \lambda_c g_c $ |
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches," Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.
(ID 15130)
Modeling thermal conductivity in a porous medium like soil is a challenging task. In this study, a wide range of samples was analyzed, and a numerical model was developed to predict the thermal conductivity in dry soil ($\lambda_b$) based on soil textures [1].
The relationship of the thermal conductivity in dry soil ($\lambda_b$) was determined in terms of the thermal conductivity in sand ($\lambda_a$), the thermal conductivity in silt ($\lambda_i$), the thermal conductivity in clay ($\lambda_c$), and the mass fraction of sand in the sample ($g_a$), the mass fraction of silt in the sample ($g_i$), the mass fraction of clay in the sample ($g_c$), using the following formula:
| $ \lambda = \lambda_w^{\Phi} \lambda_b^{1-\Phi} e^{-\beta \Phi (1-\theta_S)^2}$ |
[1] "Physical principles and calculation methods of moisture and heat transfer in cable trenches," Brakelmann, H., etz-Report 19, 93p. (1984), Berlin; Offenbach.
(ID 15131)
ID:(2054, 0)