Estabilidade Vertical
Storyboard 
A estabilidade da coluna de água marinha depende tanto da temperatura quanto da salinidade.
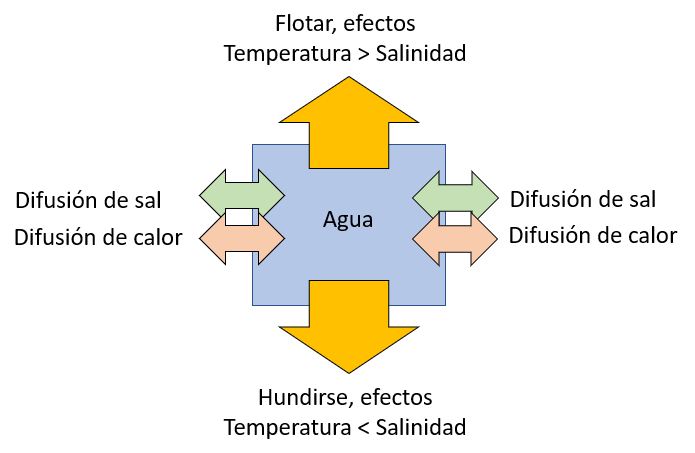
Se a temperatura aumenta, a água se expande, criando uma zona de menor densidade, levando o volume a tender a flutuar.
Por outro lado, se a salinidade aumenta, a densidade aumenta, fazendo com que o volume tenda a afundar.
Nesse sentido, existe uma competição entre os efeitos da temperatura e da salinidade, onde o volume pode tentar emergir ou afundar. Este último caso é fundamental para a geração de correntes profundas.
ID:(1524, 0)
Estabilidade Vertical
Storyboard 
A estabilidade da coluna de água marinha depende tanto da temperatura quanto da salinidade. Se a temperatura aumenta, a água se expande, criando uma zona de menor densidade, levando o volume a tender a flutuar. Por outro lado, se a salinidade aumenta, a densidade aumenta, fazendo com que o volume tenda a afundar. Nesse sentido, existe uma competição entre os efeitos da temperatura e da salinidade, onde o volume pode tentar emergir ou afundar. Este último caso é fundamental para a geração de correntes profundas.
Variáveis
Cálculos
Cálculos
Equações
Como o número Rayleigh para temperatura ($Ra_T$) depende de la aceleração gravitacional ($g$), la profundidade ($h$), la variação de temperatura ($\Delta T$), la constante de difusão do momento ($D_p$) e la constante de difusão térmica ($D_T$), conforme definido por:
e ERROR:8991 depende de o coeficiente de salinidade ($k_s$) e o fluxo crítico ($\Delta s$), conforme definido por:
ent o, podemos afirmar que
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
reduzido para:
Como la densidade da água do mar ($\rho$) igual a uma massa $m$ dividida por o volume ($V$), expressa como:
$\rho =\displaystyle\frac{m}{V}$
Se diferenciarmos essa express o para uma massa constante $m$, resultar em um ERROR:8624 como:
$\Delta\rho =-\displaystyle\frac{m}{V^2}\Delta V=-\displaystyle\frac{\rho}{V}\Delta V$
Portanto, a express o em o coeficiente de salinidade ($k_s$) com o fluxo crítico ($\Delta s$):
implica em:
Exemplos
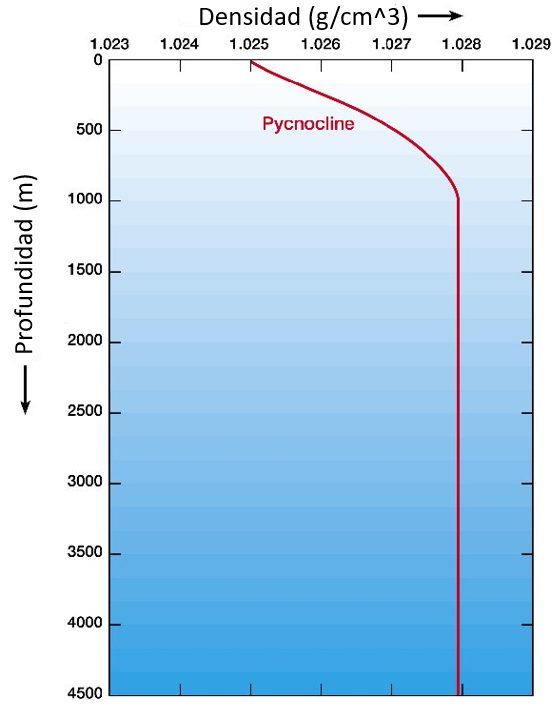
Normalmente, a densidade da gua do mar aumenta com a profundidade.
Isso significa que as camadas mais pr ximas superf cie s o mais leves do que as camadas mais profundas. Isso garante que elas flutuem sobre as camadas mais profundas e n o tendam a desloc -las.
No entanto, flutua es na temperatura e salinidade podem fazer com que as camadas mais profundas se tornem menos densas do que as camadas superiores. Isso cria uma situa o inst vel, j que essas camadas tendem a flutuar e emergir sobre as camadas superiores.
Apenas em situa es em que a densidade constante ou aumenta com a profundidade o sistema est vel.
Por outro lado, quando um sistema se torna inst vel, isso significa que, diante de uma perturba o, ele pode entrar em colapso, mas se n o for perturbado, pode manter seu estado atual.
O aumento de la variação de temperatura ($\Delta T$) leva expans o t rmica, fazendo com que la variação de volume por temperatura ($\Delta V_T$) aumente em rela o a o volume ($V$) com o coeficiente de dilatação térmica ($k_T$), como mostrado em:
Da mesma forma, o aumento de o fluxo crítico ($\Delta s$) devido massa faz com que ERROR:8624 aumente em rela o a la densidade da água do mar ($\rho$) com o coeficiente de salinidade ($k_s$), como mostrado em:
Essa express o equivalente express o em que la variação de volume devido à salinidade ($\Delta V_s$) diminui (valor negativo), como mostrado em:
Portanto, o papel da temperatura e da salinidade crucial, pois podem fazer com que a coluna de gua oce nica se torne inst vel, levando um elemento de volume a come ar a flutuar ou a afundar, revertendo assim a coluna.
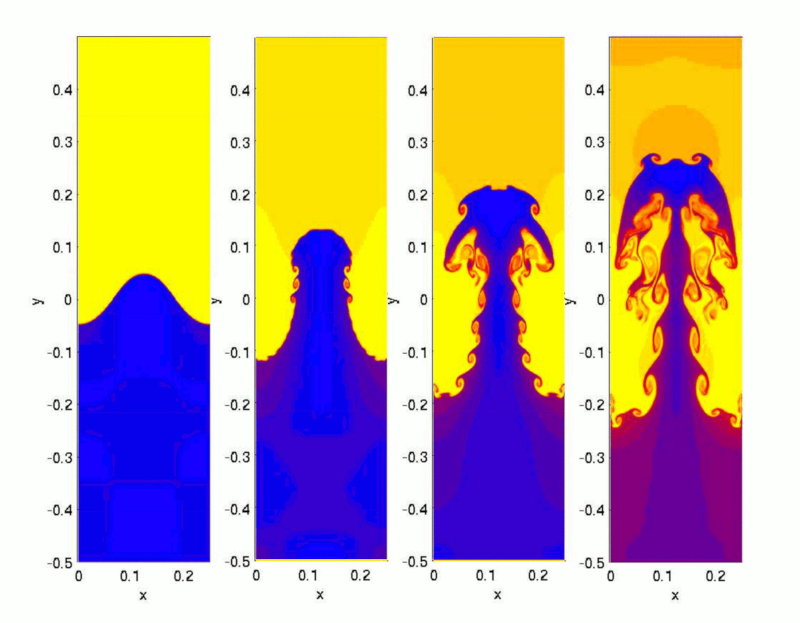
Quando aquecemos gua em uma panela, uma regi o de menor densidade se forma no fundo, pr xima fonte de calor. Essa regi o come a a subir, buscando deslocar a camada superior mais fria, que mais densa e tende a afundar.
Uma vez que a diferen a de temperatura entre a superf cie e o fundo ultrapassa um valor cr tico, verdadeiros jatos de gua quente come am a surgir, alcan ando a superf cie e criando espa o para que a gua superficial mais fria des a em dire o ao fundo:
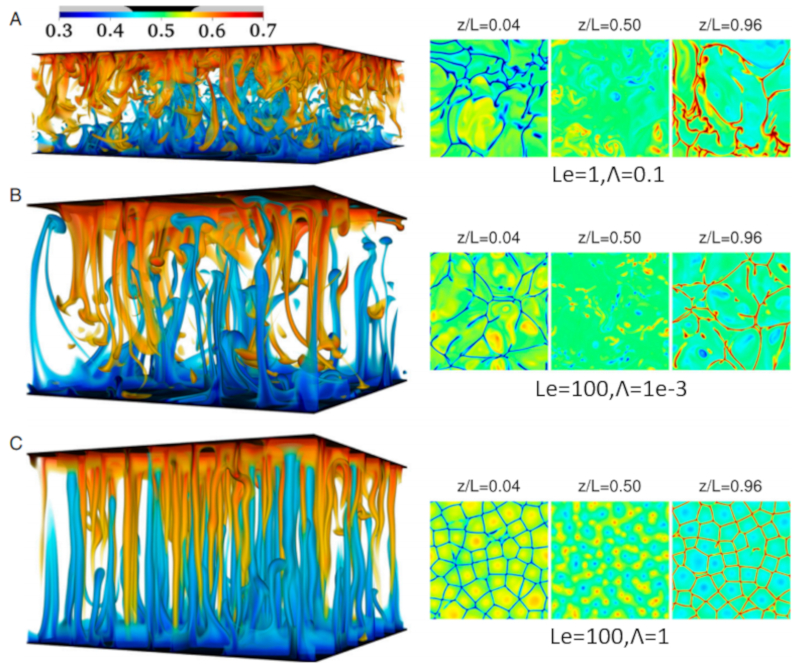
No caso da gua do mar, n o s pode haver varia es na temperatura, mas tamb m na salinidade. A salinidade geralmente aumenta a densidade, portanto, processos que reduzem a salinidade na profundidade podem levar a instabilidades.
Nesse caso, surgem regi es em que a gua com maior salinidade afunda, enquanto a gua com menor concentra o sobe. Essas regi es de afundamento de sal s o chamadas de dedos de sal e podem ser observadas no seguinte gr fico gerado por meio de simula o:
A difus o corresponde ao movimento aleat rio das mol culas, distribuindo-se gradualmente no espa o. As m ltiplas colis es fazem com que frequentemente invertam sua dire o de movimento, resultando em uma expans o muito lenta. Para descrever esse movimento, s o empregados conceitos estat sticos, como descrever a regi o onde a maioria das part culas se encontra atrav s do desvio quadr tico m dio. De fato, esse desvio quadr tico m dio aumenta linearmente no tempo:
A constante de proporcionalidade chamada de coeficiente de difus o.
Esse conceito tamb m usado para descrever como as propriedades das part culas, como momento e energia, se propagam dentro de um sistema. Nesse caso, n o ocorre altera o na distribui o espacial das part culas, mas sim na distribui o espacial do par metro considerado.
Quando a gua aquecida em uma panela, a gua pr xima ao fundo come a a se aquecer, causando sua expans o em uma variação de volume por temperatura ($\Delta V_T$) de acordo com a rela o de expans o t rmica, que atende a o coeficiente de dilatação térmica ($k_T$), o volume ($V$) e la variação de temperatura ($\Delta T$) atrav s de:
la força de empuxo ($F_b$) proporcional ao volume deslocado e pode ser aproximadamente expresso como:
$F_b \sim g \Delta V \sim k_T V \Delta T$
Ao analisarmos as unidades, podemos observar que o fator
$\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}$
o quadrado de uma constante de difus o. Portanto, a instabilidade pode ser entendida como a domin ncia de la constante de difusão do momento ($D_p$) da convec o em compara o com la constante de difusão térmica ($D_T$) necess ria para aumentar a temperatura e a perda de momento devido viscosidade.
Portanto, se a seguinte propor o:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
for muito maior do que a unidade, a convec o dominar . Nesse sentido, faz sentido definir um n mero adimensional caracter stico conhecido como o número Rayleigh para temperatura ($Ra_T$):
No caso de um sistema sem limites, foi demonstrado que o limite cr tico para a instabilidade ocorre quando o n mero de Rayleigh excede $Ra_L=657,51$. No entanto, esse limite depende da geometria do sistema, e no caso de um cilindro (como uma panela aberta), foi demonstrado que ele inst vel quando $Ra_L=1.100,65$.
A tend ncia de um elemento de gua oce nica flutuar devido ao aumento da temperatura ou afundar devido ao aumento da salinidade representada no seguinte diagrama:
Para estudar a situa o, introduzimos o fator lambda ($\Lambda$) como a propor o de o número Rayleigh para temperatura ($Ra_T$) e ERROR:8991:
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}$
Como o número Rayleigh para temperatura ($Ra_T$) depende de la aceleração gravitacional ($g$), o coeficiente de dilatação térmica ($k_T$), la variação de temperatura ($\Delta T$), la constante de difusão do momento ($D_p$) e la constante de difusão térmica ($D_T$), conforme definido pela equa o:
e ERROR:8991 depende de o coeficiente de salinidade ($k_s$), o fluxo crítico ($\Delta s$) e la constante de difusão de partículas ($D_N$), conforme definido pela equa o:
obtemos a rela o para o fator lambda ($\Lambda$) atrav s de:
ERROR:8994 compara la constante de difusão térmica ($D_T$), que depende de la condução térmica oceânica ($\lambda_T$), o calor específico ($c$) e la densidade da água do mar ($\rho$), conforme:
com la constante de difusão de partículas ($D_N$), que depende de la mobilidade de partículas ($\mu$), la constante de Boltzmann ($k_B$) e la temperatura absoluta ($T$), conforme:
Portanto, definido como:
Para manter o sistema est vel, necess rio que a difus o de energia (temperatura) e salinidade n o gerem uma la força de empuxo ($F_b$) grande o suficiente para inverter a coluna. Isso alcan ado quando o fator lambda ($\Lambda$) maior que ERROR:8994.
Portanto, o sistema est vel se a seguinte condi o for atendida:
importante observar que o fator de n mero depende da temperatura e da salinidade, ent o se essas vari veis variarem, poss vel que o sistema atinja um ponto de instabilidade.
Para modelar a convec o, devemos considerar que a gua pr xima base do sistema se aquece e, como resultado, se expande. Essa expans o o que eventualmente leva a uma diminui o da densidade e, portanto, tend ncia de flutuar. Para descrever isso, introduzimos o o coeficiente de dilatação térmica ($k_T$), que indica a propor o na qual o la variação de volume por temperatura ($\Delta V_T$) se expande em rela o ao o volume ($V$) devido ao aumento do la variação de temperatura ($\Delta T$).
Portanto, temos:
O aumento de la variação de temperatura ($\Delta T$) resulta em expans o t rmica, levando a um aumento em la variação de volume por temperatura ($\Delta V_T$) em rela o a o volume ($V$) como fun o de o coeficiente de dilatação térmica ($k_T$), como mostrado em:
Da mesma forma, adicionar sal gua leva a um aumento em o fluxo crítico ($\Delta s$) em rela o a la densidade da água do mar ($\rho$) devido ao aumento em o fluxo crítico ($\Delta s$) como fun o de o coeficiente de salinidade ($k_s$), como mostrado em:
O aumento de o fluxo crítico ($\Delta s$) provoca mudan as em ERROR:8624 em rela o a la densidade da água do mar ($\rho$) com o coeficiente de salinidade ($k_s$), como mostrado em:
Isso pode ser formulado em termos do equivalente la variação de volume devido à salinidade ($\Delta V_s$) em rela o a o volume ($V$), resultando em:
importante notar que o sinal negativo, o que significa que o aumento da salinidade leva a uma redu o efetiva do volume, fazendo com que o volume tenda a afundar.
O movimento de um sistema como a gua tende a se dissipar at que o sistema alcance o repouso em rela o ao seu entorno. Esse fen meno conhecido como viscosidade e compete com a in rcia dos corpos para manter o movimento.
O primeiro termo est associado a la viscosidade da água do oceano ($\eta$), enquanto o segundo est relacionado com a massa, ou no caso de um l quido, com la densidade da água do mar ($\rho$).
Portanto, introduzimos la constante de difusão do momento ($D_p$) com:
As unidades s o:
$\displaystyle\frac{\eta}{\rho} \rightarrow \displaystyle\frac{Pa,s}{kg/m^3} = \displaystyle\frac{m^3 kg,m,s}{s^2m^2kg} = \displaystyle\frac{m^2}{s}$
o que corresponde a uma constante de difus o. O valor para a gua est na ordem de $10^{-6} , m^2/s$.
A temperatura em um sistema como a gua tende a se difundir at que se torne uniforme em todo o volume. Essa difus o proporcional a la condução térmica oceânica ($\lambda_T$) e inversamente proporcional a la densidade da água do mar ($\rho$) e o calor específico ($c$), que s o necess rios para aumentar a temperatura.
Portanto, introduzimos la constante de difusão térmica ($D_T$) como:
As unidades s o:
$\displaystyle\frac{\lambda_T}{\rho,c} \rightarrow \displaystyle\frac{J/m,s,K}{kg/m^3,J/kg K} = \displaystyle\frac{m^2}{s}$
o que corresponde a uma constante de difus o. O valor para a gua est na ordem de $10^{-6} , m^2/s$.
A difus o de part culas, como o sal, ocorre de forma lenta devido intera o das part culas com o meio. Esse processo depende, por um lado, de la mobilidade de partículas ($\mu$), expresso em $(m/s)/N=kg/s$, que corresponde velocidade que uma part cula alcan a quando uma for a aplicada. Por outro lado, depende de la temperatura absoluta ($T$), associado velocidade que a part cula pode atingir.
Portanto, la constante de difusão de partículas ($D_N$) para o movimento das mol culas :
onde $k_B=1.34\times 10^{-23} J/K$ La constante de Boltzmann ($k_B$).
A estabilidade depende de la força de empuxo ($F_b$), que proporcional a la variação de volume por temperatura ($\Delta V_T$), o qual, junto com la aceleração gravitacional ($g$), precisa ser comparado com la constante de difusão do momento ($D_p$) e la constante de difusão térmica ($D_T$). Se reescrevermos la variação de volume por temperatura ($\Delta V_T$) em termos de expans o t rmica com o coeficiente de dilatação térmica ($k_T$), onde o volume ($V$) expresso como o cubo de la profundidade ($h$), obtemos:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
Desta forma, podemos definir o número Rayleigh para temperatura ($Ra_T$) em rela o temperatura:
O número Rayleigh para temperatura ($Ra_T$) representa a compara o de la variação de volume por temperatura ($\Delta V_T$) em termos de la variação de temperatura ($\Delta T$) e o coeficiente de dilatação térmica ($k_T$) com la constante de difusão térmica ($D_T$) e la constante de difusão do momento ($D_p$):
com la aceleração gravitacional ($g$). Da mesma forma, uma rela o para a salinidade pode ser estabelecida substituindo o coeficiente de dilatação térmica ($k_T$) por o coeficiente de salinidade ($k_s$) e la constante de difusão térmica ($D_T$) por la constante de difusão de partículas ($D_N$), resultando em ERROR:8991:
A chave para determinar se o volume de gua tender a flutuar ou a afundar pode ser estudada comparando a rela o entre o número Rayleigh para temperatura ($Ra_T$) e ERROR:8991, o que nos permite definir um n mero caracter stico chamado o fator lambda ($\Lambda$).
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
Usando as rela es que definem os n meros de Rayleigh, pode-se mostrar que o fator lambda ($\Lambda$) uma fun o de o coeficiente de dilatação térmica ($k_T$), o coeficiente de salinidade ($k_s$) e la variação de temperatura ($\Delta T$) com o fluxo crítico ($\Delta s$):
ERROR:8994 compara la constante de difusão térmica ($D_T$) com la constante de difusão de partículas ($D_N$) atrav s de:
O sistema est vel desde que o fator lambda ($\Lambda$) seja maior que ERROR:8994, pois, nesse caso, a difus o de energia (temperatura) e salinidade n o conseguem desestabilizar a coluna:
ID:(1524, 0)