Vertikale Stabilität
Storyboard 
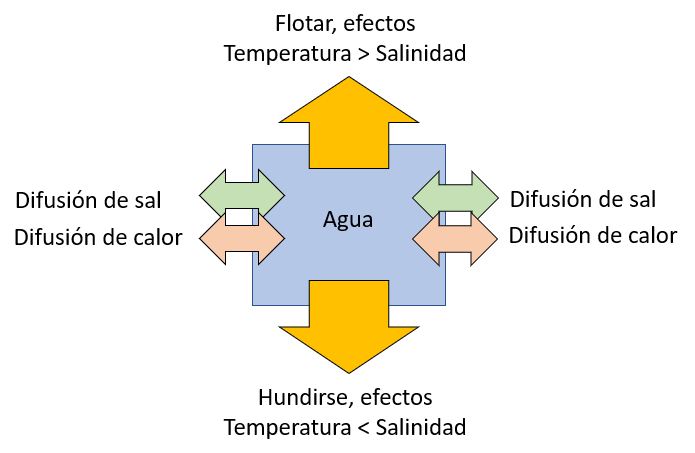
Die Stabilität der Wassersäule im Meer hängt sowohl von der Temperatur als auch von der Salinität ab.
Wenn die Temperatur steigt, dehnt sich das Wasser aus und bildet eine Zone mit geringerer Dichte, wodurch das Volumen dazu neigt, zu schwimmen.
Wenn hingegen die Salinität steigt, nimmt die Dichte zu, wodurch das Volumen dazu neigt, zu sinken.
In diesem Sinne gibt es einen Wettbewerb zwischen den Auswirkungen von Temperatur und Salinität, bei dem das Volumen versuchen kann, aufzutauchen oder zu sinken. Der letztere Fall ist entscheidend für die Bildung von Tiefenströmungen.
ID:(1524, 0)
Vertikale Stabilität
Storyboard 
Die Stabilität der Wassersäule im Meer hängt sowohl von der Temperatur als auch von der Salinität ab. Wenn die Temperatur steigt, dehnt sich das Wasser aus und bildet eine Zone mit geringerer Dichte, wodurch das Volumen dazu neigt, zu schwimmen. Wenn hingegen die Salinität steigt, nimmt die Dichte zu, wodurch das Volumen dazu neigt, zu sinken. In diesem Sinne gibt es einen Wettbewerb zwischen den Auswirkungen von Temperatur und Salinität, bei dem das Volumen versuchen kann, aufzutauchen oder zu sinken. Der letztere Fall ist entscheidend für die Bildung von Tiefenströmungen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Da der Rayleigh-Zahl für Temperatur ($Ra_T$) von die Gravitationsbeschleunigung ($g$), die Tiefe ($h$), die Temperaturschwankungen ($\Delta T$), die Diffusionskonstante des Moments ($D_p$) und die Wärmediffusionskonstante ($D_T$) abh ngt, wie definiert durch:
und der Numero de Rayleigh para la salinidad ($Ra_s$) von der Salzgehaltskoeffizient ($k_s$) und die Variación de la salinidad ($\Delta s$) abh ngt, wie definiert durch:
dann k nnen wir behaupten, dass
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
reduziert wird auf:
Da die Dichte des Meerwassers ($\rho$) gleich einer Masse $m$ geteilt durch der Volumen ($V$) ist, ausgedr ckt als:
$\rho =\displaystyle\frac{m}{V}$
Wenn wir diesen Ausdruck f r eine konstante Masse $m$ differenzieren, ergibt sich ein ERROR:8624 als:
$\Delta\rho =-\displaystyle\frac{m}{V^2}\Delta V=-\displaystyle\frac{\rho}{V}\Delta V$
Daher impliziert der Ausdruck in der Salzgehaltskoeffizient ($k_s$) mit die Variación de la salinidad ($\Delta s$):
folgendes:
Beispiele
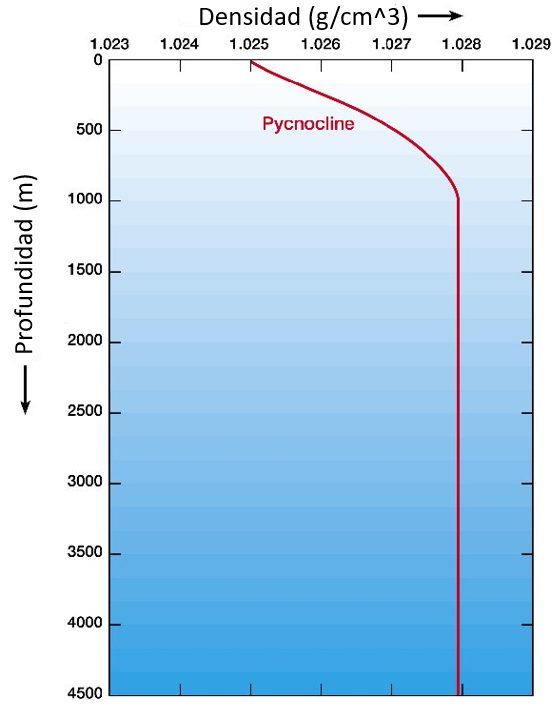
Normalerweise nimmt die Dichte des Meerwassers mit der Tiefe zu.
Das bedeutet, dass die Schichten nahe der Oberfl che leichter sind als die tieferen Schichten. Dadurch schwimmen diese Schichten ber den tieferen Schichten und neigen nicht dazu, sie zu verdr ngen.
Jedoch k nnen Schwankungen in Temperatur und Salinit t dazu f hren, dass die tieferen Schichten eine geringere Dichte als die oberen Schichten aufweisen. Dies schafft eine instabile Situation, da diese Schichten dazu neigen, ber den oberen Schichten zu schwimmen und aufzutauchen.
Nur in Situationen, in denen die Dichte konstant ist oder mit der Tiefe zunimmt, ist das System stabil.
Andererseits bedeutet die Instabilit t eines Systems, dass es bei einer St rung zusammenbrechen kann, aber wenn es nicht gest rt wird, kann es seinen aktuellen Zustand beibehalten.
Die Zunahme von die Temperaturschwankungen ($\Delta T$) f hrt zu thermischer Ausdehnung, wodurch die Volumenvariation je nach Temperatur ($\Delta V_T$) im Verh ltnis zu der Volumen ($V$) mit der Koeffizient der thermischen Ausdehnung ($k_T$) zunimmt, wie in folgender Gleichung gezeigt:
Ebenso f hrt die Zunahme von die Variación de la salinidad ($\Delta s$) aufgrund der Masse dazu, dass ERROR:8624 im Verh ltnis zu die Dichte des Meerwassers ($\rho$) mit der Salzgehaltskoeffizient ($k_s$) zunimmt, wie in folgender Gleichung gezeigt:
Dieser Ausdruck entspricht dem Ausdruck, in dem die Volumenschwankungen aufgrund des Salzgehalts ($\Delta V_s$) abnimmt (negativer Wert), wie in folgender Gleichung gezeigt:
Daher ist die Rolle von Temperatur und Salinit t entscheidend, da sie dazu f hren k nnen, dass die ozeanische Wassers ule instabil wird, wodurch ein Volumenelement zu schwimmen oder zu sinken beginnt und die S ule umgekehrt wird.
Wenn Wasser in einem Topf erhitzt wird, bildet sich im Bereich des Bodens in der N he der W rmequelle eine Region mit geringerer Dichte. Diese Region beginnt aufzusteigen und versucht, die k hlere, dichtere Schicht dar ber zu verdr ngen, die wiederum dazu neigt, abzusinken.
Sobald der Temperaturunterschied zwischen der Oberfl che und dem Boden einen kritischen Wert berschreitet, bilden sich echte Strahlen hei eres Wasser, die an die Oberfl che gelangen und Platz f r das Absteigen des k hleren Oberfl chenwassers in Richtung des Bodens schaffen:
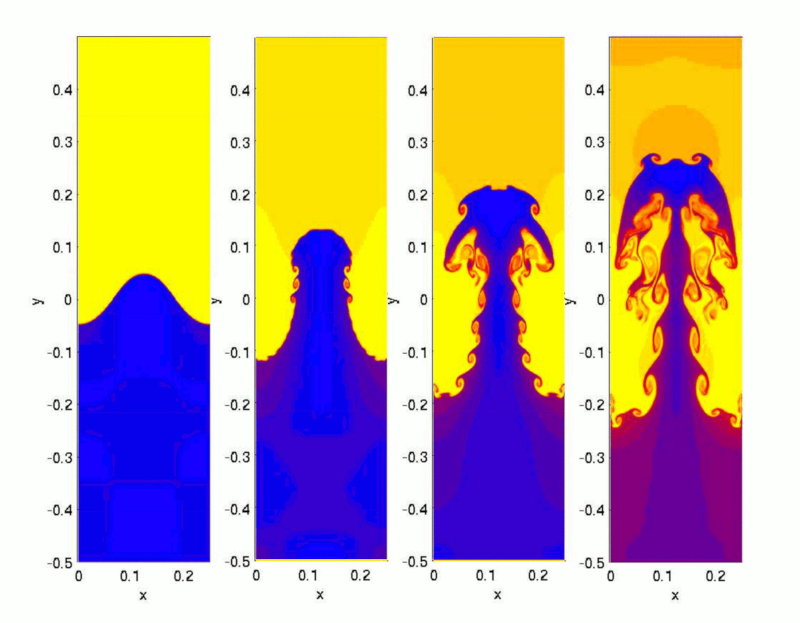
Im Fall von Meerwasser kann es nicht nur Variationen in der Temperatur geben, sondern auch in der Salinit t. Die Salinit t erh ht in der Regel die Dichte, daher k nnen Prozesse, die die Salinit t in der Tiefe verringern, zu Instabilit ten f hren.
In diesem Fall entstehen Zonen, in denen Wasser mit h herer Salinit t absinkt, w hrend Wasser mit geringerer Konzentration aufsteigt. Diese absinkenden Salzzonen werden als Salzfinger bezeichnet und sind in der folgenden Grafik dargestellt, die durch Simulation erstellt wurde:
Diffusion entspricht der zuf lligen Bewegung von Molek len, die sich allm hlich im Raum verteilen. Die Vielzahl an Kollisionen f hrt dazu, dass die Molek le h ufig ihre Bewegungsrichtung ndern und sich dadurch langsam ausdehnen. Um diese Bewegung zu beschreiben, werden statistische Konzepte verwendet, wie zum Beispiel die Beschreibung des Bereichs, in dem sich die Mehrheit der Partikel befindet, mithilfe der mittleren quadratischen Abweichung. Tats chlich nimmt diese mittlere quadratische Abweichung im Laufe der Zeit linear zu:
Die Proportionalit tskonstante wird als Diffusionskoeffizient bezeichnet.
Dieses Konzept wird auch verwendet, um zu beschreiben, wie sich Eigenschaften von Partikeln wie Impuls und Energie in einem System ausbreiten. Dabei bleibt die r umliche Verteilung der Partikel unver ndert, jedoch wird die r umliche Verteilung des betrachteten Parameters beeinflusst.
Wenn Wasser in einem Topf erhitzt wird, beginnt das Wasser in der N he des Bodens warm zu werden, was dazu f hrt, dass es sich entsprechend der thermischen Ausdehnungsbeziehung um eine Volumenvariation je nach Temperatur ($\Delta V_T$) ausdehnt, die der Koeffizient der thermischen Ausdehnung ($k_T$), der Volumen ($V$) und die Temperaturschwankungen ($\Delta T$) erf llt durch:
die Auftriebskraft ($F_b$) ist proportional zum verdr ngten Volumen und kann ungef hr ausgedr ckt werden als:
$F_b \sim g \Delta V \sim k_T V \Delta T$
Durch Analyse der Einheiten k nnen wir feststellen, dass der Faktor
$\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}$
das Quadrat einer Diffusionskonstante ist. Daher kann Instabilit t als die Dominanz von die Diffusionskonstante des Moments ($D_p$) der Konvektion im Vergleich zu die Wärmediffusionskonstante ($D_T$), die erforderlich ist, um die Temperatur zu erh hen, und dem Impulsverlust aufgrund der Viskosit t verstanden werden.
Daher, wenn das folgende Verh ltnis:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
viel gr er als eins ist, wird die Konvektion dominieren. In diesem Sinne macht es Sinn, eine charakteristische dimensionslose Zahl zu definieren, die als der Rayleigh-Zahl für Temperatur ($Ra_T$) bekannt ist:
Im Fall eines Systems ohne Begrenzungen wurde gezeigt, dass die kritische Grenze f r Instabilit t berschritten wird, wenn die Rayleigh-Zahl $Ra_L=657,51$ berschreitet. Dieser Grenzwert h ngt jedoch von der Geometrie des Systems ab, und im Fall eines Zylinders (wie eines offenen Topfes) wurde gezeigt, dass er instabil wird, wenn $Ra_L=1.100,65$ ist.
Die Tendenz, dass ein Element ozeanischen Wassers aufgrund steigender Temperatur schwimmt oder aufgrund steigender Salinit t sinkt, wird im folgenden Diagramm dargestellt:
Um die Situation zu untersuchen, f hren wir der Lambda-Faktor ($\Lambda$) als das Verh ltnis von der Rayleigh-Zahl für Temperatur ($Ra_T$) und der Numero de Rayleigh para la salinidad ($Ra_s$) ein:
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}$
Da der Rayleigh-Zahl für Temperatur ($Ra_T$) von die Gravitationsbeschleunigung ($g$), der Koeffizient der thermischen Ausdehnung ($k_T$), die Temperaturschwankungen ($\Delta T$), die Diffusionskonstante des Moments ($D_p$) und die Wärmediffusionskonstante ($D_T$) abh ngt, wie durch die Gleichung definiert:
und der Numero de Rayleigh para la salinidad ($Ra_s$) von der Salzgehaltskoeffizient ($k_s$), die Variación de la salinidad ($\Delta s$) und die Partikeldiffusionskonstante ($D_N$) abh ngt, wie durch die Gleichung definiert:
erhalten wir die Beziehung f r der Lambda-Faktor ($\Lambda$) durch:
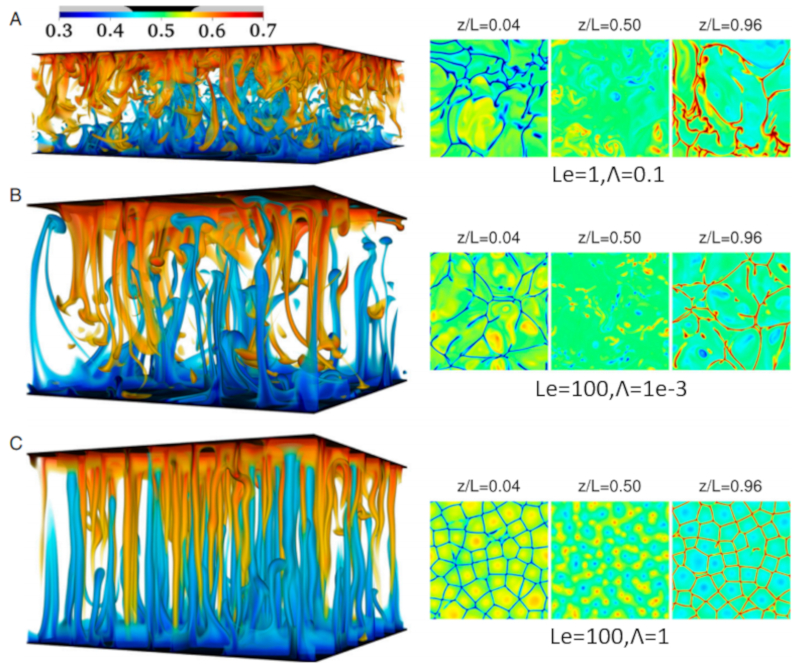
Der Numero de Lewis ($Le$) vergleicht die Wärmediffusionskonstante ($D_T$), die von die Wärmeleitung im Ozean ($\lambda_T$), der Spezifische Wärme ($c$) und die Dichte des Meerwassers ($\rho$) abh ngt, wie folgt:
mit die Partikeldiffusionskonstante ($D_N$), die von die Teilchenmobilität ($\mu$), die Boltzmann-Konstante ($k_B$) und die Absolute Temperatur ($T$) abh ngt, wie folgt:
Daher wird sie definiert als:
Um das System stabil zu halten, ist es erforderlich, dass die Diffusion von Energie (Temperatur) und Salinit t keine die Auftriebskraft ($F_b$) erzeugen, die gro genug ist, um die S ule umzukehren. Dies wird erreicht, wenn der Lambda-Faktor ($\Lambda$) gr er ist als der Numero de Lewis ($Le$).
Daher ist das System stabil, wenn folgende Bedingung erf llt ist:
Es ist wichtig zu beachten, dass der Faktor der Zahl von Temperatur und Salinit t abh ngt. Wenn sich diese Variablen also ndern, kann das System einen instabilen Zustand erreichen.
Um Konvektion zu modellieren, m ssen wir ber cksichtigen, dass das Wasser in der N he der Basis des Systems erw rmt wird und sich infolgedessen ausdehnt. Diese Ausdehnung f hrt letztendlich zu einer Abnahme der Dichte und damit zur Tendenz zu schwimmen. Um dies zu beschreiben, wird der Koeffizient der thermischen Ausdehnung ($k_T$) eingef hrt, was den Anteil angibt, um den die Volumenvariation je nach Temperatur ($\Delta V_T$) im Verh ltnis zu der Volumen ($V$) aufgrund des Anstiegs von die Temperaturschwankungen ($\Delta T$) expandiert.
Deshalb haben wir:
Die Zunahme von die Temperaturschwankungen ($\Delta T$) f hrt zu thermischer Ausdehnung, was zu einem Anstieg von die Volumenvariation je nach Temperatur ($\Delta V_T$) im Verh ltnis zu der Volumen ($V$) als Funktion von der Koeffizient der thermischen Ausdehnung ($k_T$) f hrt, wie in der folgenden Gleichung dargestellt:
hnlich f hrt das Hinzuf gen von Salz zu Wasser zu einem Anstieg von die Variación de la salinidad ($\Delta s$) im Verh ltnis zu die Dichte des Meerwassers ($\rho$) aufgrund des Anstiegs von die Variación de la salinidad ($\Delta s$) als Funktion von der Salzgehaltskoeffizient ($k_s$), wie in der folgenden Gleichung gezeigt:
Die Zunahme von die Variación de la salinidad ($\Delta s$) f hrt zu Ver nderungen in ERROR:8624 relativ zu die Dichte des Meerwassers ($\rho$) mit der Salzgehaltskoeffizient ($k_s$), wie in der folgenden Gleichung dargestellt:
Dies kann formuliert werden in Bezug auf das quivalent die Volumenschwankungen aufgrund des Salzgehalts ($\Delta V_s$) bez glich der Volumen ($V$), was zu folgender Formulierung f hrt:
Es ist wichtig zu beachten, dass das Vorzeichen negativ ist, was bedeutet, dass die Zunahme der Salinit t zu einer effektiven Volumenreduzierung f hrt und das Volumen dazu neigt, zu sinken.
Die Bewegung eines Systems wie Wasser neigt dazu, sich zu verbreiten, bis das System in Bezug auf seine Umgebung zur Ruhe kommt. Dieses Ph nomen wird als Viskosit t bezeichnet und konkurriert mit der Tr gheit von K rpern, um die Bewegung aufrechtzuerhalten.
Der erste Begriff ist mit die Viskosität von Meerwasser ($\eta$) verbunden, w hrend der zweite mit der Masse oder im Fall einer Fl ssigkeit mit die Dichte des Meerwassers ($\rho$) zusammenh ngt.
Daher f hren wir die Diffusionskonstante des Moments ($D_p$) ein mit:
Die Einheiten sind:
$\displaystyle\frac{\eta}{\rho} \rightarrow \displaystyle\frac{Pa,s}{kg/m^3} = \displaystyle\frac{m^3 kg,m,s}{s^2m^2kg} = \displaystyle\frac{m^2}{s}$
was einer Diffusionskonstante entspricht. Der Wert f r Wasser liegt in der Gr enordnung von $10^{-6} , m^2/s$.
Die Temperatur in einem System wie Wasser neigt dazu, sich zu verbreiten, bis sie im gesamten Volumen gleichm ig ist. Diese Diffusion ist proportional zu die Wärmeleitung im Ozean ($\lambda_T$) und invers proportional zu die Dichte des Meerwassers ($\rho$) und der Spezifische Wärme ($c$), die erforderlich sind, um die Temperatur zu erh hen.
Daher f hren wir die Wärmediffusionskonstante ($D_T$) ein als:
Die Einheiten sind:
$\displaystyle\frac{\lambda_T}{\rho,c} \rightarrow \displaystyle\frac{J/m,s,K}{kg/m^3,J/kg K} = \displaystyle\frac{m^2}{s}$
was einer Diffusionskonstante entspricht. Der Wert f r Wasser liegt in der Gr enordnung von $10^{-6} , m^2/s$.
Die Diffusion von Partikeln, wie zum Beispiel Salz, erfolgt langsam aufgrund der Wechselwirkung der Partikel mit dem Medium. Dieser Prozess h ngt einerseits von die Teilchenmobilität ($\mu$) ab, der in $(m/s)/N=kg/s$ ausgedr ckt wird und der Geschwindigkeit entspricht, die ein Teilchen erreicht, wenn eine Kraft angewendet wird. Andererseits h ngt er von die Absolute Temperatur ($T$) ab, der mit der Geschwindigkeit verbunden ist, die das Teilchen erreichen kann.
Daher ist die Partikeldiffusionskonstante ($D_N$) f r die Bewegung der Molek le:
wobei $k_B=1.34\times 10^{-23} J/K$ Die Boltzmann-Konstante ($k_B$) ist.
Die Stabilit t h ngt von die Auftriebskraft ($F_b$) ab, die proportional zu die Volumenvariation je nach Temperatur ($\Delta V_T$) ist, welches zusammen mit die Gravitationsbeschleunigung ($g$) mit die Diffusionskonstante des Moments ($D_p$) und die Wärmediffusionskonstante ($D_T$) verglichen werden muss. Wenn wir die Volumenvariation je nach Temperatur ($\Delta V_T$) in Bezug auf die thermische Ausdehnung mit der Koeffizient der thermischen Ausdehnung ($k_T$) neu schreiben, wobei der Volumen ($V$) als Kubus von die Tiefe ($h$) ausgedr ckt wird, erhalten wir:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
Auf diese Weise k nnen wir der Rayleigh-Zahl für Temperatur ($Ra_T$) bez glich der Temperatur definieren:
Der Rayleigh-Zahl für Temperatur ($Ra_T$) repr sentiert den Vergleich von die Volumenvariation je nach Temperatur ($\Delta V_T$) in Bezug auf die Temperaturschwankungen ($\Delta T$) und der Koeffizient der thermischen Ausdehnung ($k_T$) mit die Wärmediffusionskonstante ($D_T$) und die Diffusionskonstante des Moments ($D_p$):
mit die Gravitationsbeschleunigung ($g$). Analog dazu kann eine Beziehung f r die Salinit t hergestellt werden, indem man der Koeffizient der thermischen Ausdehnung ($k_T$) durch der Salzgehaltskoeffizient ($k_s$) und die Wärmediffusionskonstante ($D_T$) durch die Partikeldiffusionskonstante ($D_N$) ersetzt, was zu der Numero de Rayleigh para la salinidad ($Ra_s$) f hrt:
Der Schl ssel zur Bestimmung, ob das Volumen des Wassers dazu neigt zu schwimmen oder zu sinken, kann durch den Vergleich der Beziehung zwischen der Rayleigh-Zahl für Temperatur ($Ra_T$) und der Numero de Rayleigh para la salinidad ($Ra_s$) untersucht werden, was es uns erm glicht, eine charakteristische Zahl namens der Lambda-Faktor ($\Lambda$) zu definieren.
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
Durch die Verwendung der Beziehungen, die die Rayleigh-Zahlen definieren, kann gezeigt werden, dass der Lambda-Faktor ($\Lambda$) eine Funktion von der Koeffizient der thermischen Ausdehnung ($k_T$), der Salzgehaltskoeffizient ($k_s$) und die Temperaturschwankungen ($\Delta T$) mit die Variación de la salinidad ($\Delta s$) ist:
Der Numero de Lewis ($Le$) vergleicht die Wärmediffusionskonstante ($D_T$) mit die Partikeldiffusionskonstante ($D_N$) durch:
Das System ist stabil, solange der Lambda-Faktor ($\Lambda$) gr er ist als der Numero de Lewis ($Le$), da in diesem Fall die Diffusion von Energie (Temperatur) und Salinit t die S ule nicht destabilisiert:
ID:(1524, 0)