Stabilité verticale
Storyboard 
La stabilité de la colonne d'eau marine dépend à la fois de la température et de la salinité.
Si la température augmente, l'eau se dilate, créant une zone de moindre densité, ce qui fait que le volume a tendance à flotter.
En revanche, si la salinité augmente, la densité augmente, ce qui fait que le volume a tendance à s'enfoncer.
Dans ce sens, il y a une compétition entre les effets de la température et de la salinité, où le volume peut tenter d'émerger ou de s'enfoncer. Ce dernier cas est crucial pour la génération de courants profonds.
ID:(1524, 0)
Stabilité verticale
Storyboard 
La stabilité de la colonne d'eau marine dépend à la fois de la température et de la salinité. Si la température augmente, l'eau se dilate, créant une zone de moindre densité, ce qui fait que le volume a tendance à flotter. En revanche, si la salinité augmente, la densité augmente, ce qui fait que le volume a tendance à s'enfoncer. Dans ce sens, il y a une compétition entre les effets de la température et de la salinité, où le volume peut tenter d'émerger ou de s'enfoncer. Ce dernier cas est crucial pour la génération de courants profonds.
Variables
Calculs
Calculs
Équations
Puisque le nombre de Rayleigh pour la température ($Ra_T$) d pend de a accélération gravitationnelle ($g$), a profondeur ($h$), a variation de température ($\Delta T$), a constante de diffusion du moment ($D_p$) et a constante de diffusion thermique ($D_T$), comme d fini par :
et que ERROR:8991 d pend de le coefficient de salinité ($k_s$) et le débit critique ($\Delta s$), comme d fini par :
alors, nous pouvons affirmer que
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
est r duit :
Comme a densité de l'eau de mer ($\rho$) est gal une masse $m$ divis e par le volume ($V$), exprim e comme :
$\rho =\displaystyle\frac{m}{V}$
Si nous diff rencions cette expression pour une masse constante $m$, cela entra ne un ERROR:8624 comme :
$\Delta\rho =-\displaystyle\frac{m}{V^2}\Delta V=-\displaystyle\frac{\rho}{V}\Delta V$
Par cons quent, l'expression en le coefficient de salinité ($k_s$) avec le débit critique ($\Delta s$) :
implique :
Exemples
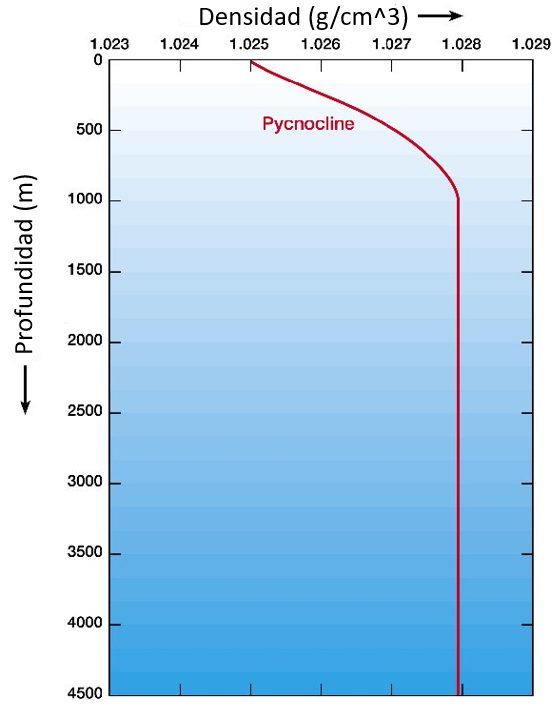
G n ralement, la densit de l'eau de mer augmente avec la profondeur.
Cela signifie que les couches proches de la surface sont plus l g res que les couches plus profondes. Cela garantit que ces couches flottent au-dessus des couches plus profondes et n\'ont pas tendance les d placer.
Cependant, les fluctuations de temp rature et de salinit peuvent entra ner des couches plus profondes ayant une densit inf rieure aux couches sup rieures. Cela cr e une situation instable, car ces couches ont tendance flotter et merger au-dessus des couches sup rieures.
Seules les situations o la densit est constante ou augmente avec la profondeur rendent le syst me stable.
D\'autre part, lorsqu\'un syst me devient instable, cela signifie qu\'en pr sence d\'une perturbation, il peut s\'effondrer, mais s\'il n\'est pas perturb , il peut maintenir son tat actuel.
L'augmentation de a variation de température ($\Delta T$) entra ne une expansion thermique, ce qui fait que a variation du volume selon la température ($\Delta V_T$) augmente par rapport le volume ($V$) avec le coefficient de dilatation thermique ($k_T$), comme illustr dans :
De m me, l'augmentation de le débit critique ($\Delta s$) due la masse fait que ERROR:8624 augmente par rapport a densité de l'eau de mer ($\rho$) avec le coefficient de salinité ($k_s$), comme illustr dans :
Cette expression est quivalente l'expression dans laquelle a variation de volume due à la salinité ($\Delta V_s$) diminue (valeur n gative), comme illustr dans :
Par cons quent, le r le de la temp rature et de la salinit est crucial, car ils peuvent rendre la colonne d'eau oc anique instable, amenant un l ment de volume commencer flotter ou couler, inversant ainsi la colonne.
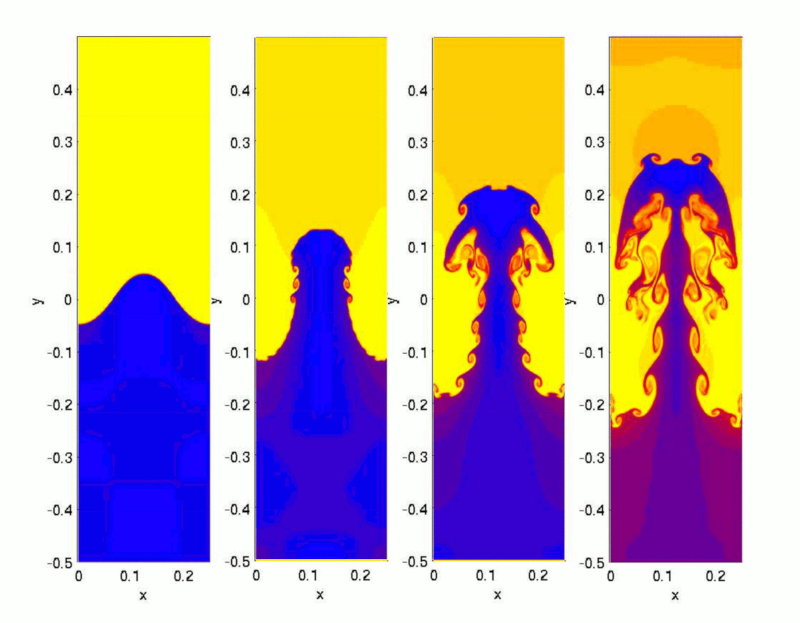
Lorsque l'eau est chauff e dans une casserole, une zone de densit plus faible se forme au fond, pr s de la source de chaleur. Cette zone commence s\' lever, cherchant d placer la couche sup rieure plus froide, qui est plus dense et tend s\'enfoncer.
Une fois que la diff rence de temp rature entre la surface et le fond d passe une valeur critique, de v ritables jets d\'eau chaude commencent merger, atteignant la surface et cr ant de l\'espace pour que l\'eau superficielle plus froide descende vers le fond:
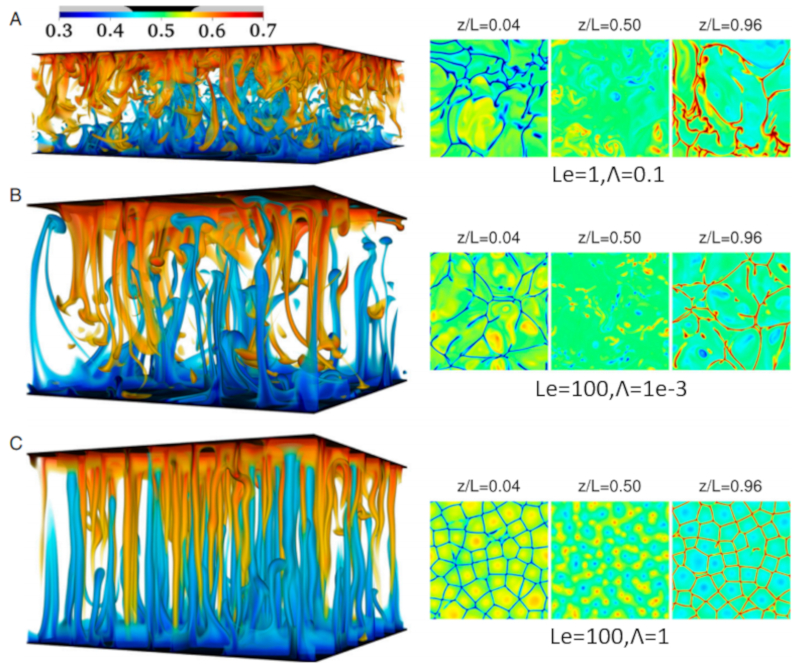
Dans le cas de l'eau de mer, il peut y avoir non seulement des variations de temp rature, mais aussi de salinit . La salinit augmente g n ralement la densit , de sorte que des processus r duisant la salinit en profondeur peuvent entra ner des instabilit s.
Dans ce cas, des zones se forment o l\'eau plus haute salinit descend tandis que l\'eau concentration plus faible monte. Ces zones de descente de sel sont appel es doigts de sel et peuvent tre observ es sur le graphique suivant, g n r par simulation:
La diffusion correspond au mouvement al atoire des mol cules se r partissant progressivement dans l'espace. Les multiples collisions font que ces mol cules changent fr quemment de direction de d placement, ce qui entra ne une expansion tr s lente. Pour d crire ce mouvement, on utilise des concepts statistiques tels que la d viation quadratique moyenne pour d crire la zone o se trouvent la majorit des particules. En fait, cette d viation quadratique moyenne augmente lin airement dans le temps :
La constante de proportionnalit est appel e le coefficient de diffusion.
Ce concept est galement utilis pour d crire comment les propri t s des particules, telles que la quantit de mouvement et l\' nergie, se propagent l\'int rieur d\'un syst me. Dans ce cas, la distribution spatiale des particules ne change pas, mais c\'est la distribution spatiale du param tre consid r qui est affect e.
Lorsque l'eau est chauff e dans une casserole, l'eau pr s du fond commence se r chauffer, ce qui entra ne son expansion de une variation du volume selon la température ($\Delta V_T$) selon la relation d'expansion thermique, qui satisfait le coefficient de dilatation thermique ($k_T$), le volume ($V$) et a variation de température ($\Delta T$) travers :
a force de poussée ($F_b$) est proportionnelle au volume d plac et peut tre approximativement exprim e comme :
$F_b \sim g \Delta V \sim k_T V \Delta T$
En analysant les unit s, nous pouvons observer que le facteur
$\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}$
est le carr d'une constante de diffusion. Par cons quent, l'instabilit peut tre comprise comme la pr dominance de a constante de diffusion du moment ($D_p$) de la convection par rapport a constante de diffusion thermique ($D_T$) n cessaire pour augmenter la temp rature et la perte de moment due la viscosit .
Ainsi, si la proportion suivante :
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
est nettement sup rieure l'unit , la convection dominera. Dans ce sens, il est logique de d finir un nombre adimensionnel caract ristique connu sous le nom de le nombre de Rayleigh pour la température ($Ra_T$) :
Dans le cas d'un syst me sans limites, il a t d montr que la limite critique pour l'instabilit survient lorsque le nombre de Rayleigh d passe $Ra_L=657,51$. Cependant, cette limite d pend de la g om trie du syst me, et dans le cas d'un cylindre (comme une casserole ouverte), il a t d montr qu'il est instable lorsque $Ra_L=1.100,65$.
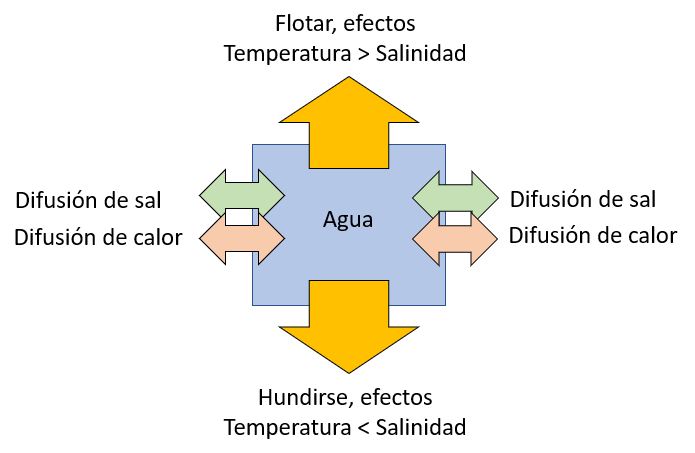
La tendance d'un l ment d'eau oc anique flotter en raison de l'augmentation de la temp rature ou couler en raison de l'augmentation de la salinit est repr sent e dans le diagramme suivant :
Pour tudier la situation, nous introduisons le facteur lambda ($\Lambda$) comme la proportion de le nombre de Rayleigh pour la température ($Ra_T$) et ERROR:8991 :
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}$
Puisque le nombre de Rayleigh pour la température ($Ra_T$) d pend de a accélération gravitationnelle ($g$), le coefficient de dilatation thermique ($k_T$), a variation de température ($\Delta T$), a constante de diffusion du moment ($D_p$) et a constante de diffusion thermique ($D_T$), tel que d fini par l' quation :
et que ERROR:8991 d pend de le coefficient de salinité ($k_s$), le débit critique ($\Delta s$) et a constante de diffusion des particules ($D_N$), tel que d fini par l' quation :
nous obtenons la relation pour le facteur lambda ($\Lambda$) par :
ERROR:8994 compare a constante de diffusion thermique ($D_T$), qui d pend de a conduction thermique des océans ($\lambda_T$), le chaleur spécifique ($c$) et a densité de l'eau de mer ($\rho$), comme suit :
avec a constante de diffusion des particules ($D_N$), qui d pend de a mobilité des particules ($\mu$), a constante de Boltzmann ($k_B$) et a température absolue ($T$), comme suit :
Par cons quent, il est d fini comme suit :
Pour maintenir le syst me stable, il est n cessaire que la diffusion de l' nergie (temp rature) et de la salinit ne g n rent pas une a force de poussée ($F_b$) suffisamment grande pour inverser la colonne. Cela est atteint lorsque le facteur lambda ($\Lambda$) est sup rieur ERROR:8994.
Par cons quent, le syst me est stable si la condition suivante est remplie :
Il est important de noter que le facteur de nombre d pend de la temp rature et de la salinit , donc si ces variables varient, le syst me peut atteindre un point d'instabilit .
Pour mod liser la convection, nous devons consid rer que l'eau pr s de la base du syst me se r chauffe et, par cons quent, se dilate. Cette expansion est ce qui conduit finalement une diminution de la densit et, donc, la tendance flotter. Pour d crire cela, nous introduisons le coefficient de dilatation thermique ($k_T$), qui indique la proportion selon laquelle a variation du volume selon la température ($\Delta V_T$) se dilate par rapport le volume ($V$) en raison de l'augmentation de a variation de température ($\Delta T$).
Donc, nous avons :
L'augmentation de a variation de température ($\Delta T$) entra ne une expansion thermique, conduisant une augmentation de a variation du volume selon la température ($\Delta V_T$) par rapport le volume ($V$) en fonction de le coefficient de dilatation thermique ($k_T$), comme illustr dans :
De m me, l'ajout de sel l'eau conduit une augmentation de le débit critique ($\Delta s$) par rapport a densité de l'eau de mer ($\rho$) en raison de l'augmentation de le débit critique ($\Delta s$) en fonction de le coefficient de salinité ($k_s$), comme illustr dans :
L'augmentation de le débit critique ($\Delta s$) entra ne des changements dans ERROR:8624 par rapport a densité de l'eau de mer ($\rho$) avec le coefficient de salinité ($k_s$), comme illustr dans :
Cela peut tre formul en termes de l' quivalent a variation de volume due à la salinité ($\Delta V_s$) par rapport le volume ($V$), ce qui donne :
Il est important de noter que le signe est n gatif, ce qui signifie que l'augmentation de la salinit conduit une r duction effective du volume, faisant en sorte que le volume tende s'enfoncer.
Le mouvement d'un syst me tel que l'eau a tendance se dissiper jusqu' ce que le syst me atteigne le repos par rapport son environnement. Ce ph nom ne est connu sous le nom de viscosit et entre en comp tition avec l'inertie des corps pour maintenir le mouvement.
Le premier terme est associ a viscosité de l'eau des océans ($\eta$), tandis que le second est li la masse, ou dans le cas d'un liquide, a densité de l'eau de mer ($\rho$).
Par cons quent, nous introduisons a constante de diffusion du moment ($D_p$) avec :
Les unit s sont :
$\displaystyle\frac{\eta}{\rho} \rightarrow \displaystyle\frac{Pa,s}{kg/m^3} = \displaystyle\frac{m^3 kg,m,s}{s^2m^2kg} = \displaystyle\frac{m^2}{s}$
ce qui correspond une constante de diffusion. La valeur pour l'eau est de l'ordre de $10^{-6} , m^2/s$.
La temp rature dans un syst me comme l'eau a tendance se diffuser jusqu' ce qu'elle soit uniforme dans tout le volume. Cette diffusion est proportionnelle a conduction thermique des océans ($\lambda_T$) et inversement proportionnelle a densité de l'eau de mer ($\rho$) et le chaleur spécifique ($c$), qui sont n cessaires pour augmenter la temp rature.
Par cons quent, nous introduisons a constante de diffusion thermique ($D_T$) comme:
Les unit s sont:
$\displaystyle\frac{\lambda_T}{\rho,c} \rightarrow \displaystyle\frac{J/m,s,K}{kg/m^3,J/kg K} = \displaystyle\frac{m^2}{s}$
ce qui correspond une constante de diffusion. La valeur pour l'eau est de l'ordre de $10^{-6} , m^2/s$.
La diffusion des particules, comme le sel, se produit lentement en raison de l'interaction des particules avec le milieu. Ce processus d pend, d'une part, de a mobilité des particules ($\mu$), exprim en $(m/s)/N=kg/s$, ce qui correspond la vitesse qu'une particule atteint lorsqu'une force est appliqu e. D'autre part, il d pend de a température absolue ($T$), associ la vitesse que la particule peut atteindre.
Par cons quent, a constante de diffusion des particules ($D_N$) pour le mouvement des mol cules est :
o $k_B=1.34\times 10^{-23} J/K$ est a constante de Boltzmann ($k_B$).
La stabilit d pend de a force de poussée ($F_b$), qui est proportionnelle a variation du volume selon la température ($\Delta V_T$), lequel, avec a accélération gravitationnelle ($g$), doit tre compar a constante de diffusion du moment ($D_p$) et a constante de diffusion thermique ($D_T$). Si nous r crivons a variation du volume selon la température ($\Delta V_T$) en termes d'expansion thermique avec le coefficient de dilatation thermique ($k_T$), o le volume ($V$) est exprim comme le cube de a profondeur ($h$), nous obtenons :
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
De cette fa on, nous pouvons d finir le nombre de Rayleigh pour la température ($Ra_T$) par rapport la temp rature :
Le nombre de Rayleigh pour la température ($Ra_T$) repr sente la comparaison de a variation du volume selon la température ($\Delta V_T$) en termes de a variation de température ($\Delta T$) et le coefficient de dilatation thermique ($k_T$) avec a constante de diffusion thermique ($D_T$) et a constante de diffusion du moment ($D_p$) :
avec a accélération gravitationnelle ($g$). De m me, une relation pour la salinit peut tre tablie en rempla ant le coefficient de dilatation thermique ($k_T$) par le coefficient de salinité ($k_s$) et a constante de diffusion thermique ($D_T$) par a constante de diffusion des particules ($D_N$), ce qui donne ERROR:8991 :
La cl pour d terminer si le volume d'eau tendra flotter ou couler peut tre tudi e en comparant la relation entre le nombre de Rayleigh pour la température ($Ra_T$) et ERROR:8991, ce qui nous permet de d finir un nombre caract ristique appel le facteur lambda ($\Lambda$).
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
En utilisant les relations d finissant les nombres de Rayleigh, on peut montrer que le facteur lambda ($\Lambda$) est une fonction de le coefficient de dilatation thermique ($k_T$), le coefficient de salinité ($k_s$) et a variation de température ($\Delta T$) avec le débit critique ($\Delta s$) :
ERROR:8994 compare a constante de diffusion thermique ($D_T$) avec a constante de diffusion des particules ($D_N$) travers :
Le syst me est stable tant que le facteur lambda ($\Lambda$) est sup rieur ERROR:8994, car dans ce cas, la diffusion d' nergie (temp rature) et de salinit ne parviennent pas d stabiliser la colonne :
ID:(1524, 0)