mechanisms

The change in gravitational acceleration leads to a flow of water that tends to alter the height of the water column (sea depth) in order to compensate for pressure:

image

Variations in acceleration lead to changes in water pressure around the planet, allowing water columns to differ in heights.

In particular, the deviations caused are as follows:

For the sun's case: 8.14 cm, 16.28 cm
For the moon's case: 17.9 cm, 35.6 cm

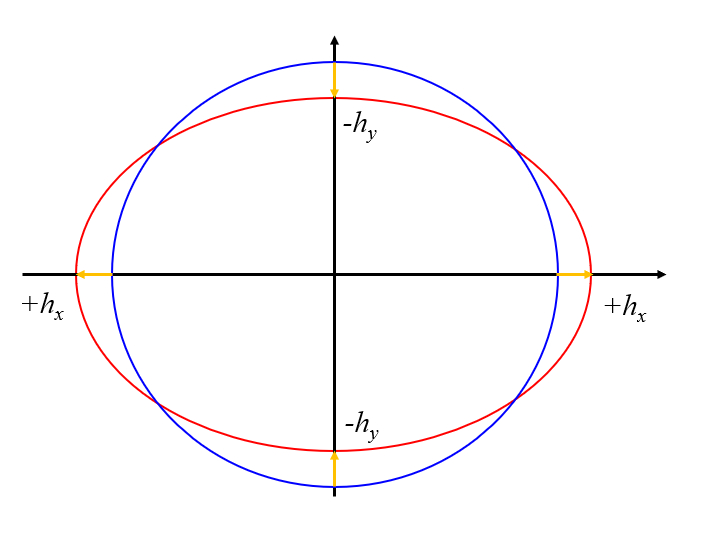
This situation can be represented as a deformation of a circle, corresponding to an ellipse.

image

In the case of the sun,

image

the following parameters are considered:

Mass: 1.987e+30 kg
Sun-Earth distance: 1.50e+11 m

The tidal heights can be calculated using the following relationships:

For the x-direction, with list=11653, we have:

And for the y-direction, with list=11654, we obtain:

$h_y = 8.14 cm$

And at the point of maximum tide ($\theta = 0$), it is:

$h_x = 16.28 cm$

Thus, the fluctuations due to the sun amount to $h_x + h_y = 24.42 cm$.

In the case of the Moon,

image

we have the following parameters:

Mass: 7.349e+22 kg
Distance Earth-Moon: 3.84e+8 m

For the x-direction, with list=11653, we have:

And for the y-direction, with list=11654, we have:

$h_y = 17.9 cm$

And at the point of highest tide ($\theta = 0$), we have:

$h_x = 35.6 cm$

So, the fluctuations due to the Moon amount to $h_x + h_y = 53.5 cm$.

model

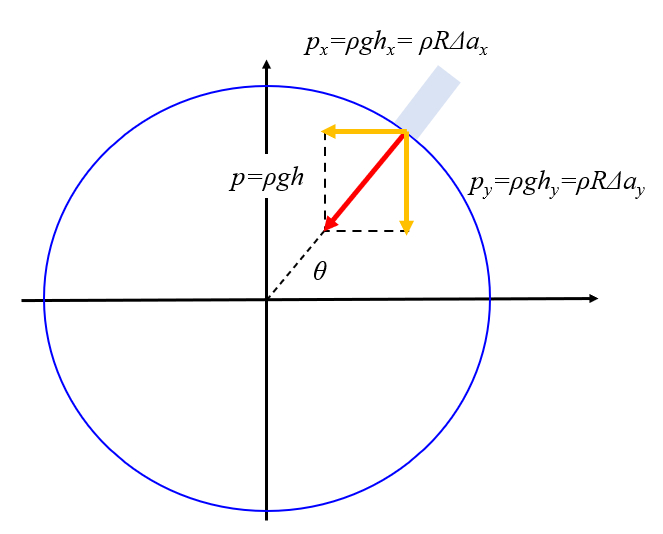
The change in acceleration means that the water column experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$

Therefore,

kyon

The change in acceleration implies that the column of water experiences a different pressure unless the depth adjusts. Achieving a steady state involves precisely this. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

equation=13215

With the variation on the conjunction side with list=11650

and with list=11649

It follows that the surface rises with list in

where only the variable part of the variation was taken into account, since the term $GM/d^2$ acts on the entire system and does not create differences.

The change in acceleration implies that the column of water experiences a different pressure unless the depth adjusts. Achieving a steady state involves precisely this. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

$p_y=\rho g h_y=\rho\Delta a_{cy} R$

Therefore, it follows that:

kyon

The change in acceleration means that the column of water experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:

equation=13216

With the variation on the side of conjunction with list=11645

As a result, the surface rises with list at

With the variation in sea level due to lunar and/or solar tides, which is a function of the universal Gravitation Constant ($G$), the planet radio ($R$), the celestial object planet distance ($d$), the gravitational Acceleration ($g$), and the latitude of the place ($\theta$), the tidal height in the direction of the celestial body causing the tide is given by the height of the tide in the direction of the star ($h_x$), calculated as follows:

equation=11653

In the perpendicular direction, the corresponding height is the height of the tide perpendicular to the direction towards the star ($h_y$):

equation=11654

Therefore, the total difference is obtained from the height of the tide in the direction of the star ($h_x$) and the height of the tide perpendicular to the direction towards the star ($h_y$):

kyon