User:
Lunar-solar tidal overlap and continent effect
Storyboard 
The overlap of lunar and solar tides leads to either more extreme tides or compensatory effects that reduce them. Additionally, there is discussion about the effect of water being unable to move freely due to the presence of continents.
ID:(1577, 0)
Lunar-solar tidal overlap and continent effect
Storyboard
The overlap of lunar and solar tides leads to either more extreme tides or compensatory effects that reduce them. Additionally, there is discussion about the effect of water being unable to move freely due to the presence of continents.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
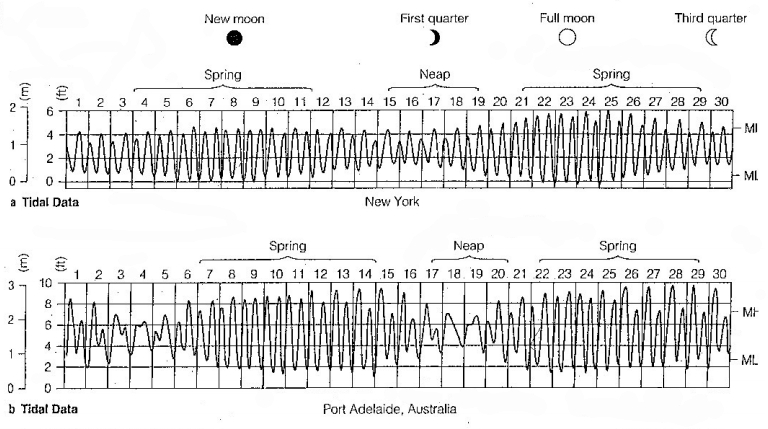
If one studies tide records worldwide, it is observed that:
• There are two tides per day.
• During full moon and new moon, tides are higher.
• During waxing and waning crescents, tides are lower.
The terms "spring tide" and "neap tide" mean:
• Spring tide = high tide
• Neap tide = low tide
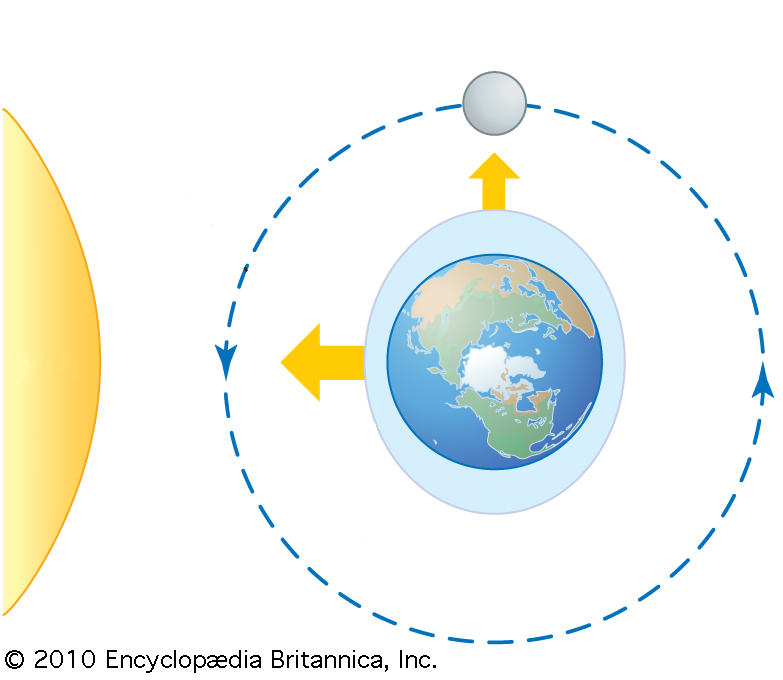
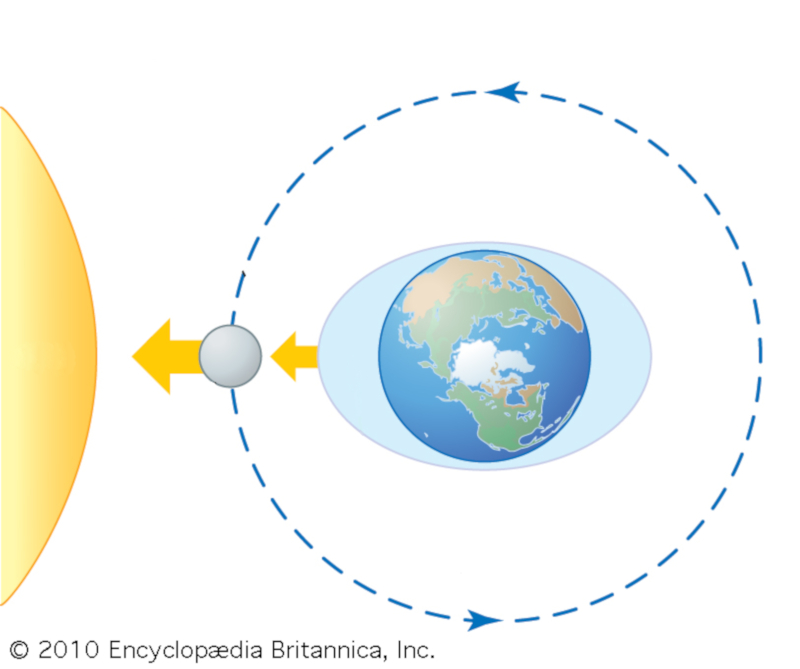
When the moon is at a right angle with respect to the Earth-Sun direction, the tides are partially counteracted. This happens every time there is a first quarter or last quarter moon.
When the sun and the moon align, the tides combine, creating a higher tide. This occurs every time there is a full moon (moon in opposition to the sun) or a new moon (moon aligned with the sun).
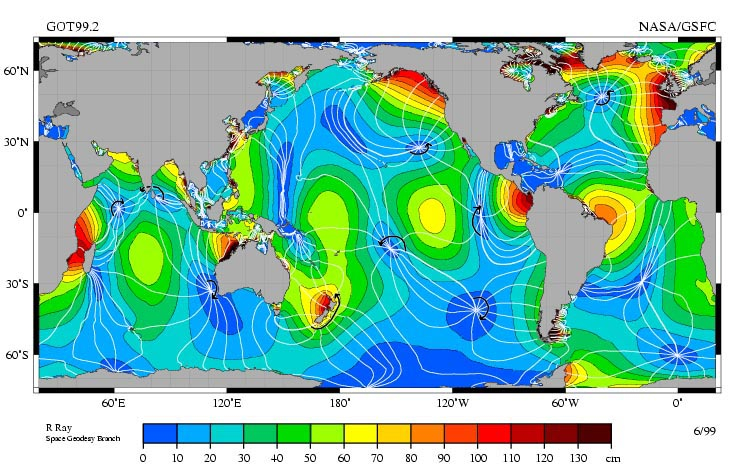
An extreme example is illustrated in the following image of Alma, New Brunswick, Canada, in the Bay of Fundy. This tide surpasses by far the maximum value that occurs when the sun and moon align (24.42 cm + 53.5 cm = 77.92 cm). The reason for this is the displacement of water, which is halted by the American continent, leading to this accumulation.
If we observe the measurements of the highest tides on the planet, we can see that:
• They occur along coastlines because water accumulates when it encounters obstacles such as the coastline.
• Waves are formed that have nodes, points where the sea level does not vary.
The change in acceleration implies that the column of water experiences a different pressure unless the depth adjusts. Achieving a steady state involves precisely this. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:
With the variation on the conjunction side with
and with
It follows that the surface rises with
where only the variable part of the variation was taken into account, since the term $GM/d^2$ acts on the entire system and does not create differences.
The change in acceleration means that the column of water experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:
With the variation on the side of conjunction with
As a result, the surface rises with
The change in acceleration implies that the column of water experiences a different pressure unless the depth adjusts. Achieving a steady state involves precisely this. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:
With the variation on the conjunction side with
and with
It follows that the surface rises with
where only the variable part of the variation was taken into account, since the term $GM/d^2$ acts on the entire system and does not create differences.
The change in acceleration means that the column of water experiences a different pressure unless the depth adjusts. To achieve a steady state, this is precisely what happens. The modification of gravitational acceleration is compensated by a change in depth corresponding to the tide:
With the variation on the side of conjunction with
As a result, the surface rises with
ID:(1577, 0)
