Fluxos de circulação profunda
Storyboard 
Existem vários pontos onde ocorrem fluxos da superfície oceânica para maiores profundidades, induzindo assim uma circulação profunda. Esta circulação está sujeita à força de Coriolis, resultando em desvios e alguns fluxos em direção à superfície (ressurgência), que estão associados às correntes de superfície.
O modelo clássico para essas correntes é o de Stommel e Arons, que, embora simples, explica os diferentes fluxos de profundidade observados.
[1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
ID:(1623, 0)
Fluxos de circulação profunda
Storyboard 
Existem vários pontos onde ocorrem fluxos da superfície oceânica para maiores profundidades, induzindo assim uma circulação profunda. Esta circulação está sujeita à força de Coriolis, resultando em desvios e alguns fluxos em direção à superfície (ressurgência), que estão associados às correntes de superfície. O modelo clássico para essas correntes é o de Stommel e Arons, que, embora simples, explica os diferentes fluxos de profundidade observados. [1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
Variáveis
Cálculos
Cálculos
Equações
Como la aceleração de Coriolis na direção x ($a_{c,x}$) composto por la velocidade angular do planeta ($\omega$), la latitude ($\varphi$), la y velocidade do objeto ($v_y$) e la z velocidade do objeto ($v_z$):
e a defini o de o fator de Coriolis ($f$) :
al m da restri o de movimento na superf cie, onde:
$v_z = 0$
resulta que la aceleração de Coriolis na direção x ($a_{c,x}$) :
Como la aceleração de Coriolis na direção y ($a_{c,y}$) composto por la velocidade angular do planeta ($\omega$), la x velocidade do objeto ($v_x$) e la latitude ($\varphi$):
e a defini o de o fator de Coriolis ($f$) :
al m da restri o de um movimento na superf cie onde:
$v_z = 0$
isso leva a que la aceleração de Coriolis na direção y ($a_{c,y}$) seja:
Se assumirmos tempos caracter sticos para cada dimens o, podemos estimar as acelera es de Coriolis como velocidades divididas pelos seus tempos caracter sticos, ou seja:
$v_i =a_i \Delta t_i$
onde
Isso nos leva a:
$v_z=\beta R v_x\Delta t_z$
Por outro lado, com a equa o para a componente
$v_x=\displaystyle\frac{v_y}{f\Delta t_y}$
Substituindo
Quando h movimento na dire o x (leste-oeste), ocorre la aceleração de Coriolis na direção z ($a_{c,z}$) com la x velocidade do objeto ($v_x$), la velocidade angular do planeta ($\omega$) e la latitude ($\varphi$):
Isso complementado por la aceleração de Coriolis na superfície, na direção x ($a_{c,x}$) (leste-oeste), com o fator de Coriolis ($f$) e la y velocidade do objeto ($v_y$):
e la aceleração de Coriolis na superfície, na direção y ($a_{c,y}$) (norte-sul) com o fator de Coriolis ($f$) e la x velocidade do objeto ($v_x$), que definido como:
Onde o fator de Coriolis ($f$) definido como:
Portanto, podemos introduzir o fator Beta Coriolis ($\beta$), definido como:
Com isso, obtemos:
Em analogia a o fator de Coriolis ($f$) definido com la latitude ($\varphi$) e la velocidade angular do planeta ($\omega$) como:
o fator varia no arco $R\theta$, com o raio do planeta ($R$) e la latitude ($\varphi$) como a latitude, de acordo com:
$\displaystyle\frac{\partial f}{\partial (R\varphi) }=\displaystyle\frac{ 2\omega\cos\varphi }{R}$
portanto, o fator Beta Coriolis ($\beta$) pode ser definido como:
Exemplos
A circula o mais profunda conhecida como circula o termohalina (Termohaline Circulation - THC), pois o seu movimento est associado a varia es de temperatura (termo) e salinidade (halina). Para compreender como isso ocorre, necess rio descrever primeiro a estrutura do sistema.
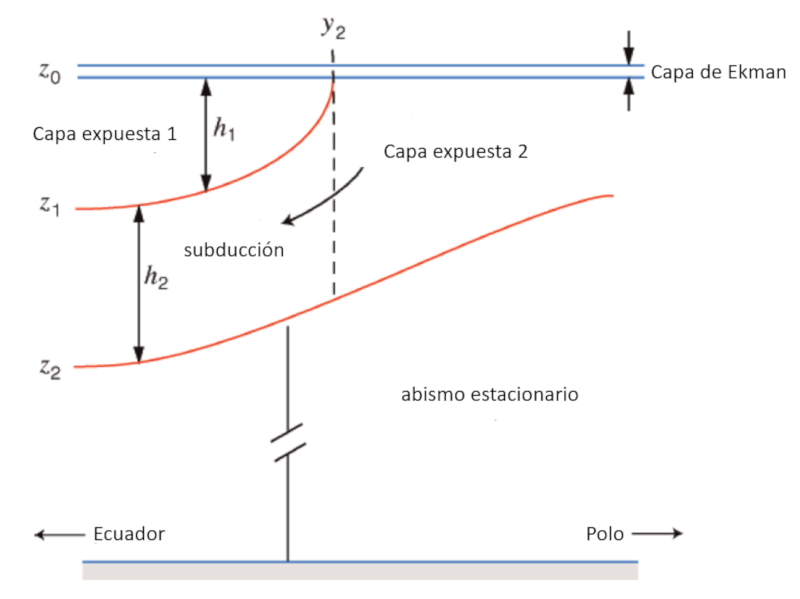
De forma simplificada, o oceano pode ser modelado como um sistema de tr s camadas:
- Uma camada superior em que o movimento da gua gerado pelas correntes de ar sobre ela.
- Uma camada intermedi ria cujo movimento gerado por diferen as de densidade nos oceanos, originadas por diferen as de temperatura e salinidade (termohalina).
- Uma camada profunda que pode ser considerada em repouso.
O aumento da densidade em dire o aos polos, onde a gua mais fria, faz com que a gua literalmente afunde, criando uma subduc o abaixo da camada superficial. O diagrama a seguir resume o que foi descrito:
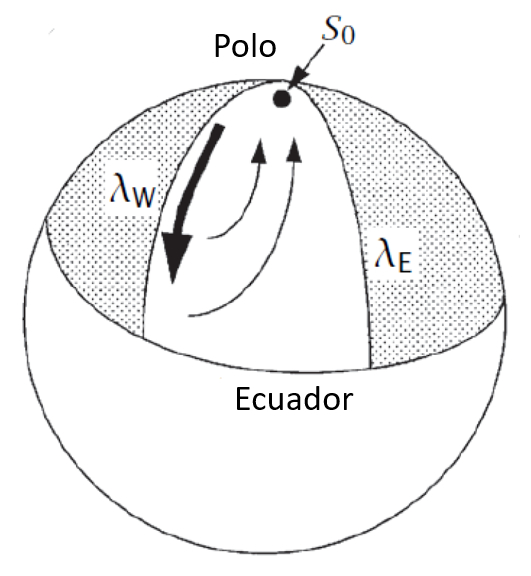
Se observarmos o globo terrestre, a circula o termohalina gerada perto de um dos polos (norte ou sul) por meio da gua que, devido a uma maior salinidade e menor temperatura, come a a afundar. Seu fluxo direcionado em dire o ao equador, havendo um afloramento que faz com que parte da gua suba e flua em dire o ao polo para suprir a gua que est descendo.
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre a circula o abissal do oceano mundial - I. Padr es estacion rios de fluxo planet rio em uma esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre a circula o abissal do oceano mundial - II. Um modelo idealizado do padr o e amplitude da circula o em bacias oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
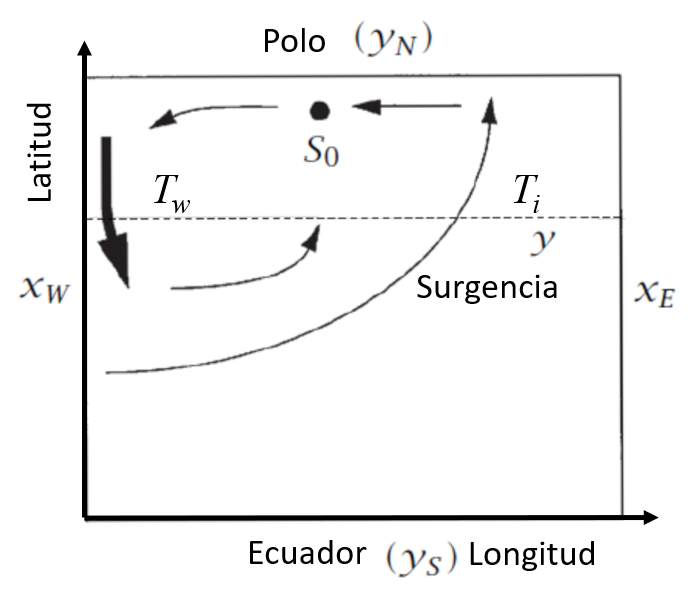
O modelo de Stommel e Arons [1], [2] considera o oceano como uma caixa bidimensional com coordenadas nos eixos x e y. Especificamente:
- Coordenadas no eixo x: $x_w$ (oeste) e $x_e$ (leste).
- Coordenadas no eixo y: $y_s$ (sul) e $y_n$ (norte).
Essas coordenadas s o representadas no seguinte gr fico:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre a circula o abissal do oceano mundial - I. Padr es estacion rios de fluxo planet rio em uma esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre a circula o abissal do oceano mundial - II. Um modelo idealizado do padr o e amplitude da circula o em bacias oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
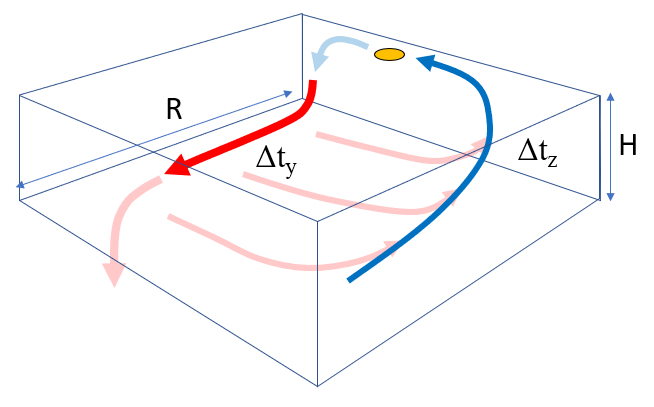
Cada etapa est associada a um tempo caracter stico:
Tempo de viagem com o fluxo principal $\Delta t_y$
Tempo de desvio com o fluxo de perda $\Delta t_x$
Tempo de surg ncia $\Delta t_z$
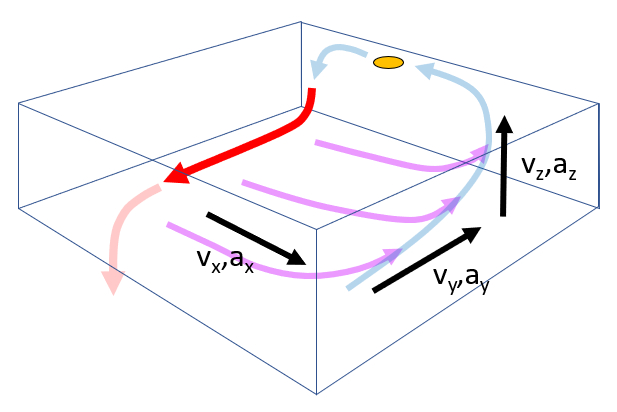
Cada tempo caracter stico est associado s velocidades e acelera es ao longo do caminho percorrido:
- Com o fluxo principal $v_y, a_y$.
- Com o fluxo de perda $v_x, a_x$.
- Com a surg ncia $v_z, a_z$.
Em geral, a velocidade inicial (
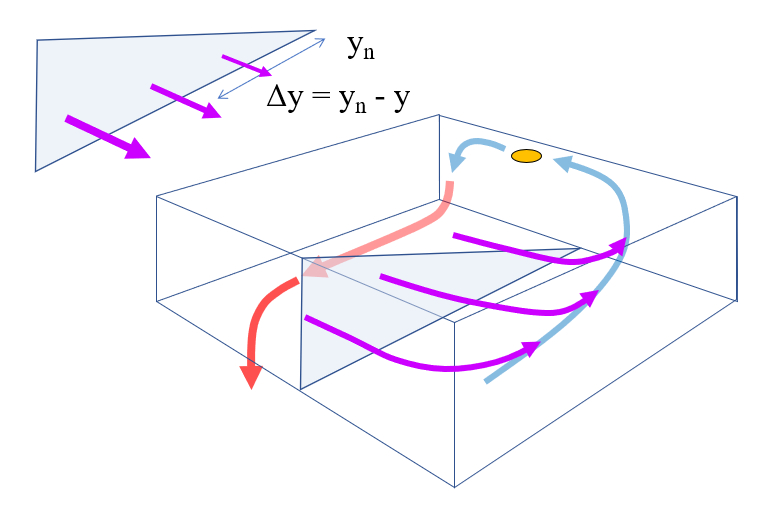
O fluxo de perda n o uniforme e distribui-se ao longo da latitude, sendo modelado em fun o da sua dist ncia em rela o posi o mais ao norte. Assim, ele nulo em latitudes do norte e m ximo na borda sul do ret ngulo onde a circula o modelada:
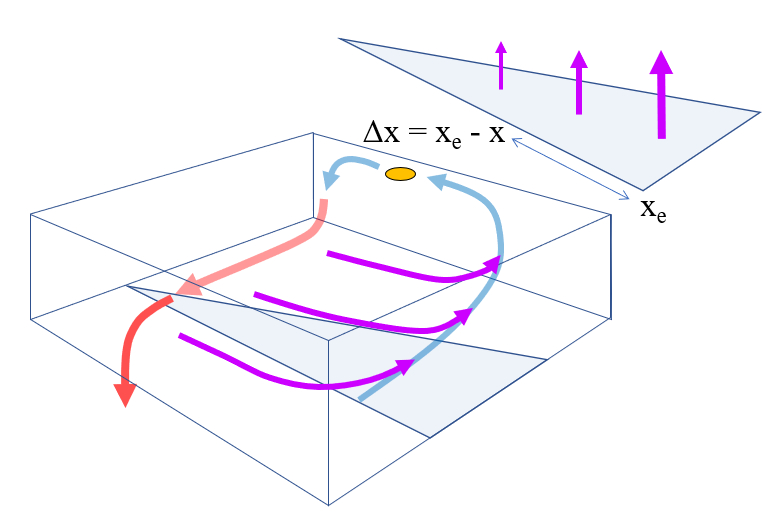
Uma vez que o fluxo de perda n o uniforme, a surg ncia tamb m n o ser . Dentro do mesmo modelo, assume-se que a surg ncia m xima na borda leste do ret ngulo onde a circula o modelada. De forma an loga perda, assume-se uma rela o linear:
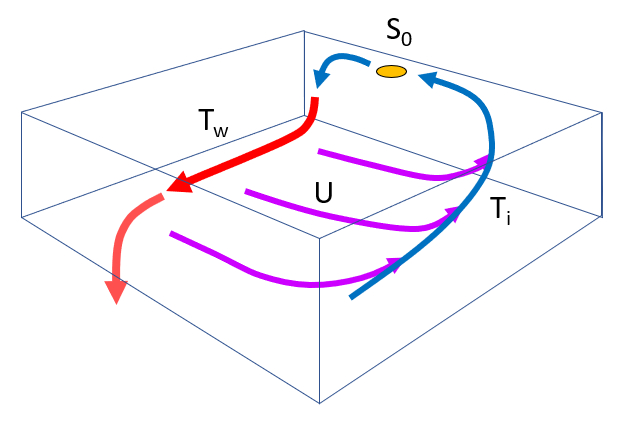
No modelo do fluxo profundo, existem quatro fluxos a serem considerados:
O fluxo principal $F_w$, que se move ao longo do fundo do mar.
O fluxo de perda $F_i$, que a fra o desviada devido for a de Coriolis.
O fluxo de surg ncia $U_x$, que corresponde fra o do fluxo de perda que atinge a superf cie.
O fluxo de afundamento $S_0$, proveniente das correntes superficiais, incluindo as perdas que voltam a afundar.
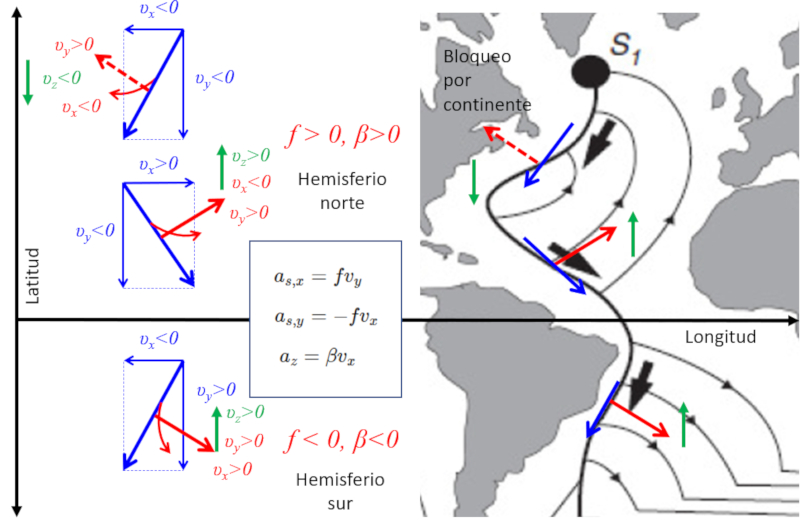
A chamada For a de Coriolis desempenha um papel essencial na din mica da gua nos polos, influenciando como as massas de gua descem devido s varia es de temperatura e salinidade.
Ao analisar o Oceano Atl ntico, pode-se observar um movimento da gua do polo em dire o ao equador, que se desvia para oeste. Esse fen meno causado pelo atraso em rela o rota o do planeta, ao passar de uma zona de menor velocidade ao longo da latitude para uma de maior velocidade. Esse comportamento pode ser modelado pela equa o de Coriolis para a dire o x, que com
Nessa equa o, o fator de Coriolis
O contorno geogr fico do continente permite um movimento na dire o x (longitude), resultando em uma acelera o na dire o y (latitude), que pode ser calculada com
Esse c lculo revela que, pr ximo ao equador, ocorrem deslocamentos que afastam a gua da corrente principal, movendo-a para o norte. Se analisarmos a acelera o na dire o z (profundidade) e considerarmos que o
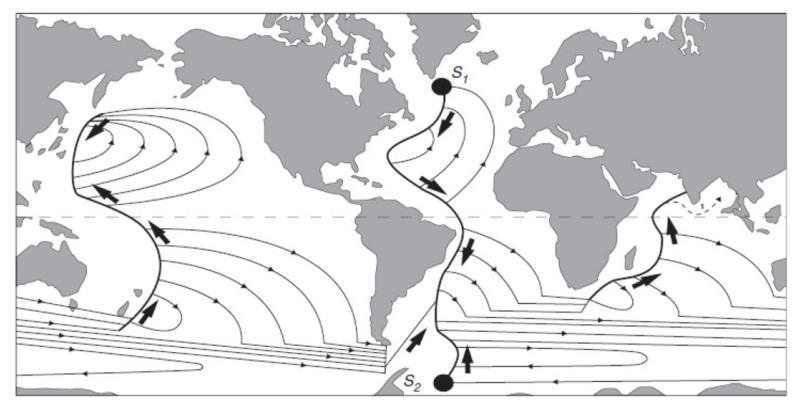
No final, Stommel e Arons [1], [2] resolvem o modelo, indicando os principais fluxos profundos que existem em todo o globo:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre a circula o abissal do oceano mundial - I. Padr es estacion rios de fluxo planet rio em uma esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre a circula o abissal do oceano mundial - II. Um modelo idealizado do padr o e amplitude da circula o em bacias oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
Quando Stommel e Arons [1], [2] desenvolveram seu primeiro modelo de circula o termohalina, eles subdividiram os diferentes oceanos em zonas com surg ncia definida (setas apontando para cima) e duas fontes, uma no rtico e outra na Ant rtica:
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sobre a circula o abissal do oceano mundial - I. Padr es estacion rios de fluxo planet rio em uma esfera.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sobre a circula o abissal do oceano mundial - II. Um modelo idealizado do padr o e amplitude da circula o em bacias oce nicas.) Deep Sea Research (1953), 6(3), 217-233.
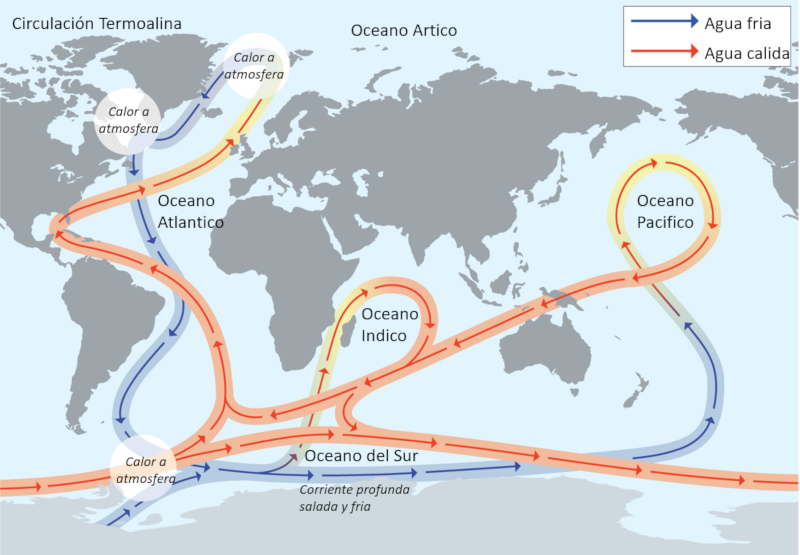
Medi es t m mostrado que a circula o termohalina um sistema integrado que abrange todo o globo. Existem pelo menos dois pontos que podem ser considerados como fontes, e seu percurso penetra todos os oceanos.
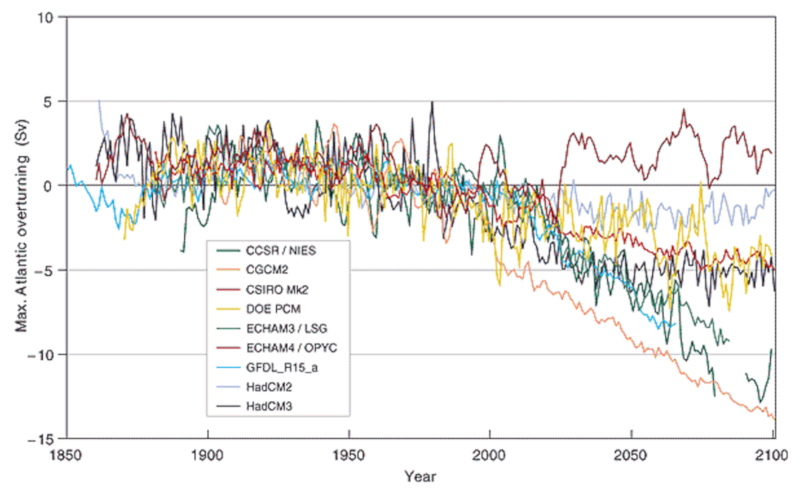
Atrav s de m ltiplas simula es, s o estudados os efeitos do derretimento do gelo polar na supress o dos afundamentos e seu impacto na circula o profunda. Existem indica es de que a circula o come ou a diminuir, no entanto, o colapso da circula o profunda n o significa necessariamente que o mesmo ocorrer com a circula o superficial, que impulsionada pelos ventos. O que pode ocorrer um deslocamento na circula o superficial, resultando em uma redu o na contribui o da Corrente do Golfo de guas quentes para o norte da Europa.
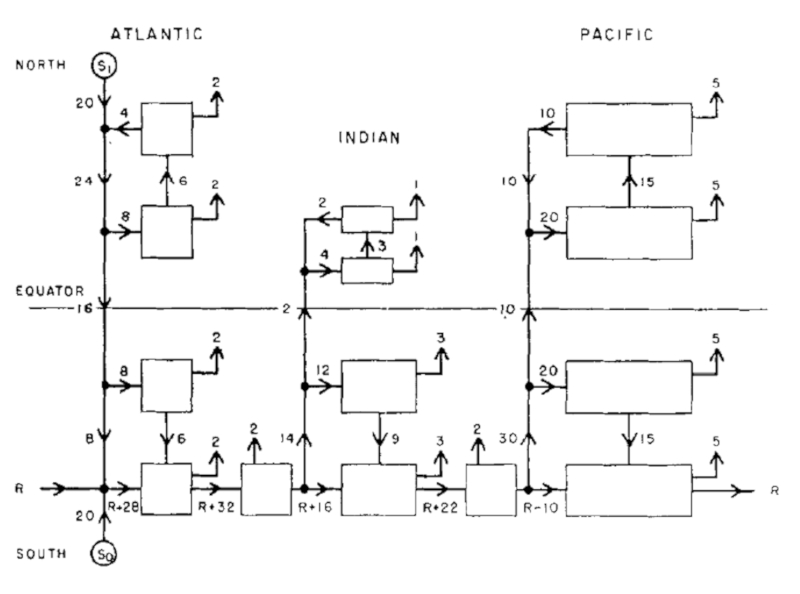
A seguir, apresentado um diagrama das varia es dos fluxos em unidades de Sv (Sverdrup), equivalente a $10^6,m^3/s$:
Assumindo uma taxa de afundamento de aproximadamente 20 Sv, conclui-se que em algumas simula es a circula o profunda interrompida. Essas varia es est o associadas a diferentes cen rios futuros de atividade humana e considera es para aspectos em que h menos certeza sobre sua ocorr ncia. Mais detalhes podem ser encontrados nos relat rios do Painel Intergovernamental sobre Mudan as Clim ticas (IPCC).
Ao modelar o Atl ntico Norte como uma caixa com um sistema de coordenadas pr ximo ao equador e na regi o do Caribe, a largura da caixa calculada subtraindo-se a posi o oeste da posi o leste:
Ao modelar o Atl ntico Norte como uma caixa com um sistema de coordenadas pr ximo ao equador e na regi o do Caribe, a altura da caixa obtida subtraindo a posi o sul da posi o norte:
Analogamente ao fator de Coriolis, podemos estudar como o fator varia ao longo do arco, o que nos leva a obter o fator Beta Coriolis ($\beta$) dado por la latitude ($\varphi$), o raio do planeta ($R$) e la velocidade angular do planeta ($\omega$) por:
Com base na rela o entre a acelera o de Coriolis e as velocidades em cada eixo, podemos estimar a acelera o da ressurg ncia que ocorrer na circula o. Utilizando a parametriza o que depende do tamanho do setor e da latitude da localiza o, obtemos la aceleração de Coriolis na direção z ($a_{c,z}$) em fun o de o fator Beta Coriolis ($\beta$), o raio do planeta ($R$) e la velocidade paralela ($v_x$):
Como la aceleração de Coriolis na direção x ($a_{c,x}$) pode ser reescrito com o fator de Coriolis ($f$) e a condi o de que n o h movimento vertical:
$v_z = 0$
ent o resulta que la aceleração de Coriolis na superfície, na direção x ($a_{c,x}$) :
Como la aceleração de Coriolis na direção x ($a_{c,x}$) pode ser reescrito com o fator de Coriolis ($f$) e sob a condi o de que n o haja movimento vertical:
$v_z = 0$
Assim, deduz-se que la aceleração de Coriolis na superfície, na direção y ($a_{c,y}$) :
O movimento ao longo de uma latitude, devido rota o da Terra, gera uma acelera o de Coriolis la aceleração de Coriolis na superfície, na direção y ($a_{c,y}$), que em o movimento característico do intervalo de tempo em $y$ ($\Delta t_y$) resulta em la velocidade no meridiano ($v_y$) conforme:
A velocidade de ressurg ncia la velocidade de ressurgência ($v_z$) determinada por la aceleração de Coriolis na direção z ($a_{c,z}$) em fun o de o movimento característico do intervalo de tempo em $z$ ($\Delta t_z$):
Para simplificar as equa es, trabalhamos com um fator de Coriolis ($f$), que uma constante para o local f sico, pois inclui la velocidade angular do planeta ($\omega$) para a Terra e la latitude ($\varphi$) para o local:
No hemisf rio sul, a latitude negativa e, com ela, 8600, o que explica por que os sistemas giram na dire o oposta ao hemisf rio norte.
A circula o do fluxo faz com que la velocidade paralela ($v_x$) tenda a ter uma magnitude semelhante a la velocidade no meridiano ($v_y$) em um giro negativo:
A continuidade do fluxo nos permite determinar como as velocidades est o relacionadas em cada fase. Dessa forma, podemos estimar la velocidade de ressurgência ($v_z$) com base em o fator Beta Coriolis ($\beta$), o fator de Coriolis ($f$), o movimento característico do intervalo de tempo em $y$ ($\Delta t_y$), o movimento característico do intervalo de tempo em $z$ ($\Delta t_z$), o raio do planeta ($R$) e la velocidade no meridiano ($v_y$):
Como a velocidade de surg ncia determinada por
e a rela o entre os tempos deve cumprir com
a velocidade no fundo dada por
A surg ncia depende da velocidade em dire o superf cie e da posi o na caixa. Uma vez que maior em dire o ao equador e relativamente uniforme ao longo da largura, ela modelada de forma a variar apenas com a dist ncia em rela o borda norte da caixa:
$y_n - y$
Portanto, com
A velocidade de surg ncia determinada usando o valor
O fluxo dentro da caixa pode ser modelado usando a equa o
Especificamente, observa-se que a velocidade de surg ncia maior em dire o borda oeste, o que pode ser representado por
con
A presen a do fator 2 no modelo considera a m dia levando em conta o gradiente existente.
O tempo na dire o
A conserva o do fluxo implica que o fluxo que se move ao longo da costa leste da Am rica, representado por $T_w$, e as componentes que sofrem afloramento, representadas por $U_x$, s o inicialmente gerados pelo volume que afunda, indicado como $S_0$, al m daqueles provenientes da circula o por meio do afloramento. Portanto, podemos expressar da seguinte forma:
Neste caso, existem dois tipos de fluxos: o fluxo superficial e o fluxo em dire o ou a partir da profundidade. Por conserva o, podemos assumir que o fluxo total que flui em dire o s profundidades no ponto S_0 deve corresponder ao fluxo total gerado pela surg ncia. Esta ltima ocorre em toda a superf cie e com velocidade vertical, portanto:
Se a velocidade for multiplicada por
com a altura
$T_i \sim v_y H \Delta x$
Portanto, com
Considerando a equa o de balan o, com
a contribui o da fonte com
o fluxo de fundo
e a surg ncia, com
Assumindo que a zona chega ao equador (
Como o fator de Coriolis dado por
ele pode ser relacionado ao fator beta com base em sua varia o ao redor de uma posi o. Isso ocorre porque, na expans o de Taylor, obtemos:
$f \sim f_0 + \frac{df}{dy}y$
onde a derivada :
$\frac{df}{dy} = 2\omega\cos\theta = \beta$
Assim, utilizando
Com
pode ser reescrita como
utilizando
ID:(1623, 0)