Flux de circulation profonde
Storyboard 
Il existe plusieurs points où des flux depuis la surface océanique vers des profondeurs plus importantes se produisent, induisant ainsi une circulation profonde. Cette circulation est soumise à la force de Coriolis, entraînant des déviations et quelques flux vers la surface (upwelling) qui sont associés aux courants de surface.
Le modèle classique pour ces courants est celui de Stommel et Arons, qui, bien que simple, explique les différents flux de profondeur observés.
[1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
ID:(1623, 0)
Flux de circulation profonde
Storyboard 
Il existe plusieurs points où des flux depuis la surface océanique vers des profondeurs plus importantes se produisent, induisant ainsi une circulation profonde. Cette circulation est soumise à la force de Coriolis, entraînant des déviations et quelques flux vers la surface (upwelling) qui sont associés aux courants de surface. Le modèle classique pour ces courants est celui de Stommel et Arons, qui, bien que simple, explique les différents flux de profondeur observés. [1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
Variables
Calculs
Calculs
Équations
Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) est compos de a vitesse angulaire de la planète ($\omega$), a latitude ($\varphi$), a y vitesse de l'objet ($v_y$) et a z vitesse de l'objet ($v_z$) :
et la d finition de le facteur de Coriolis ($f$) est :
ainsi que la contrainte de mouvement la surface o :
$v_z = 0$
il en r sulte que a accélération de Coriolis dans la direction x ($a_{c,x}$) est :
Comme a accélération de Coriolis dans la direction y ($a_{c,y}$) est compos de a vitesse angulaire de la planète ($\omega$), a x vitesse de l'objet ($v_x$) et a latitude ($\varphi$) :
et que la d finition de le facteur de Coriolis ($f$) est :
en plus de la contrainte d'un mouvement la surface o :
$v_z = 0$
cela conduit ce que a accélération de Coriolis dans la direction y ($a_{c,y}$) soit :
Si nous introduisons des chelles de temps typiques pour chaque dimension, nous pouvons estimer les acc l rations de Coriolis comme des vitesses divis es par leurs chelles de temps typiques, c'est- -dire :
$v_i =a_i \Delta t_i$
avec
Ainsi, nous avons :
$v_z=\beta R v_x\Delta t_z$
D'autre part, avec l\' quation pour la composante
$v_x=\displaystyle\frac{v_y}{f\Delta t_y}$
En rempla ant
Lorsqu'il y a un mouvement dans la direction x (est-ouest), cela produit a accélération de Coriolis dans la direction z ($a_{c,z}$) avec a x vitesse de l'objet ($v_x$), a vitesse angulaire de la planète ($\omega$) et a latitude ($\varphi$) :
Cela est compl t par a accélération de Coriolis à la surface, dans la direction x ($a_{c,x}$) (est-ouest), avec le facteur de Coriolis ($f$) et a y vitesse de l'objet ($v_y$) :
et a accélération de Coriolis à la surface, dans la direction y ($a_{c,y}$) (nord-sud) avec le facteur de Coriolis ($f$) et a x vitesse de l'objet ($v_x$), qui est d fini comme :
O Le facteur de Coriolis ($f$) est d fini comme :
Par cons quent, nous pouvons introduire le facteur bêta de Coriolis ($\beta$), d fini comme :
Avec cela, nous obtenons :
En analogie avec le facteur de Coriolis ($f$) d fini avec a latitude ($\varphi$) et a vitesse angulaire de la planète ($\omega$) comme :
le facteur varie dans l'arc $R\theta$, avec le rayon de la planète ($R$) et a latitude ($\varphi$) comme la latitude, selon :
$\displaystyle\frac{\partial f}{\partial (R\varphi) }=\displaystyle\frac{ 2\omega\cos\varphi }{R}$
ainsi le facteur bêta de Coriolis ($\beta$) peut tre d fini comme :
Exemples
La circulation en profondeur est connue sous le nom de circulation thermohaline (THC) car son mouvement est associ aux variations de temp rature (thermo) et de salinit (haline). Pour comprendre comment cela se produit, nous devons d'abord d crire la structure du syst me.
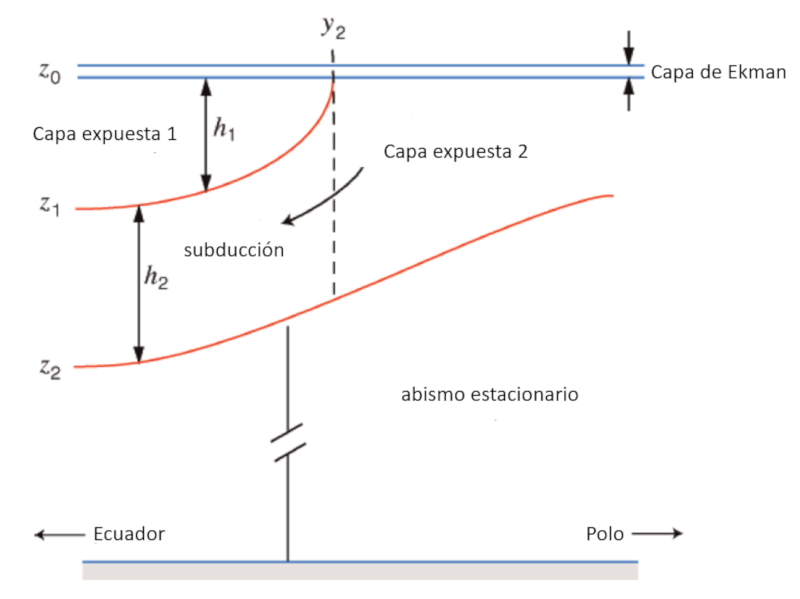
De mani re simplifi e, l\'oc an peut tre mod lis comme un syst me trois couches :
- Une couche sup rieure o le mouvement de l\'eau est g n r par les courants d\'air qui soufflent sa surface.
- Une couche interm diaire dont le mouvement est g n r par des diff rences de densit dans les oc ans, r sultant de variations de temp rature et de salinit (thermohaline).
- Une couche profonde qui peut tre consid r e comme immobile.
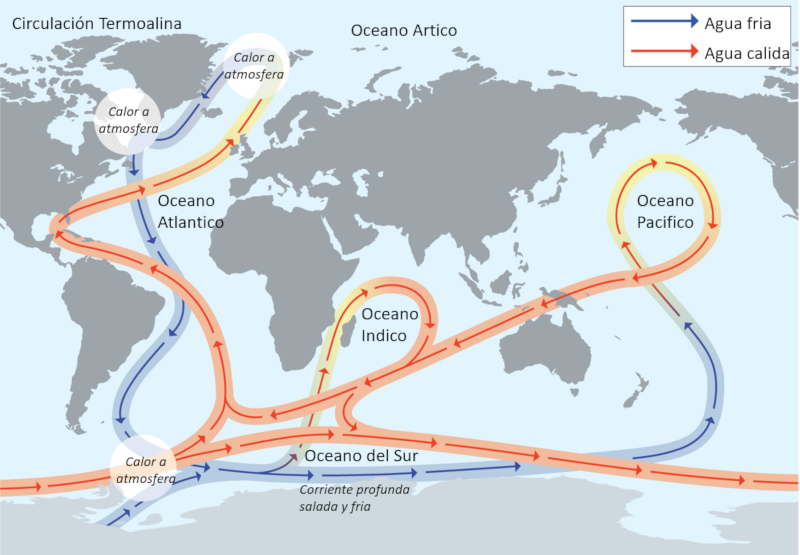
L\'augmentation de la densit vers les p les, o l\'eau est plus froide, provoque litt ralement l\'enfoncement de l\'eau, cr ant une subduction sous la couche superficielle. Le diagramme suivant r sume ce qui a t d crit:
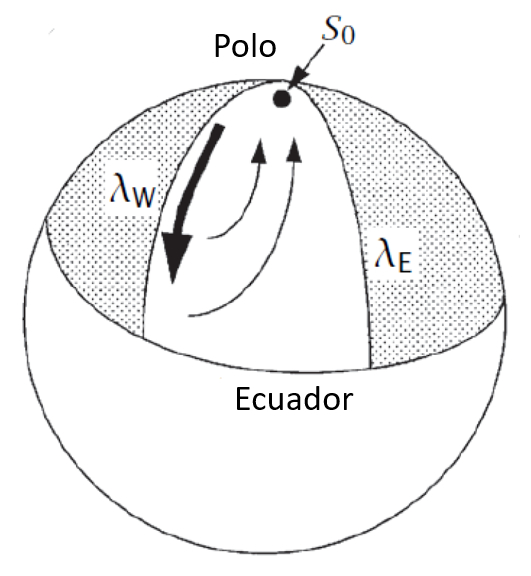
Lorsqu'on observe le globe terrestre, la circulation thermohaline se forme pr s d\'un des p les (nord ou sud) travers l\'eau qui, en raison d\'une plus grande salinit et d\'une temp rature plus basse, commence s\'enfoncer. Son flux est dirig vers l\' quateur, cr ant une remont e o une partie de l\'eau s\' l ve et s\' coule en direction du p le pour remplacer l\'eau qui descend.
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sur la circulation abyssale de l'oc an mondial - I. Sch mas de flux plan taires stationnaires sur une sph re.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sur la circulation abyssale de l'oc an mondial - II. Un mod le id alis du sch ma et de l'amplitude de la circulation dans les bassins oc aniques.) Deep Sea Research (1953), 6(3), 217-233.
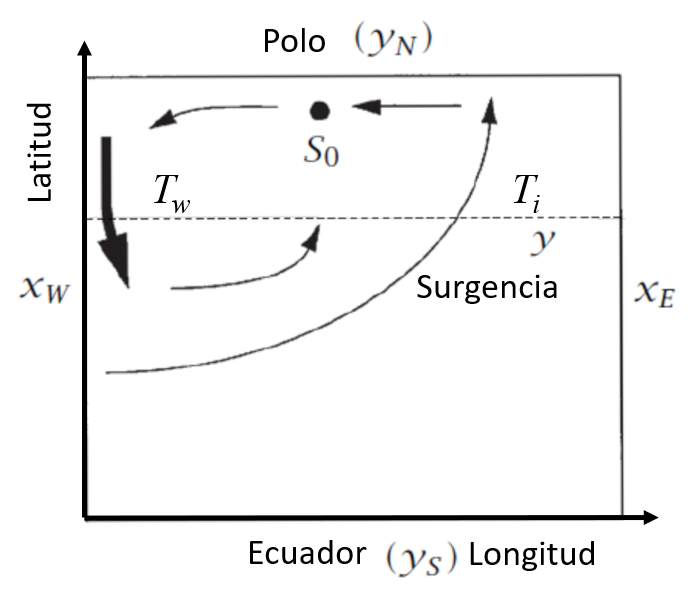
Le mod le de Stommel et Arons [1], [2] consid re l'oc an comme une bo te bidimensionnelle avec des coordonn es sur les axes x et y. Plus pr cis ment :
- Coordonn es sur l'axe x : $x_w$ (ouest) et $x_e$ (est).
- Coordonn es sur l\'axe y : $y_s$ (sud) et $y_n$ (nord).
Ces coordonn es sont repr sent es dans le graphique suivant :
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sur la circulation abyssale de l'oc an mondial - I. Sch mas de flux plan taires stationnaires sur une sph re.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sur la circulation abyssale de l'oc an mondial - II. Un mod le id alis du sch ma et de l'amplitude de la circulation dans les bassins oc aniques.) Deep Sea Research (1953), 6(3), 217-233.
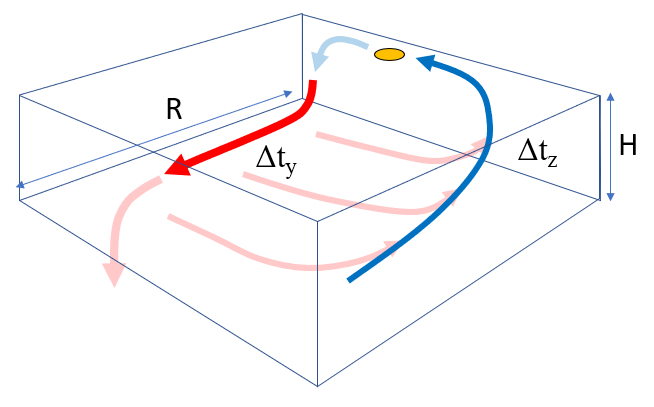
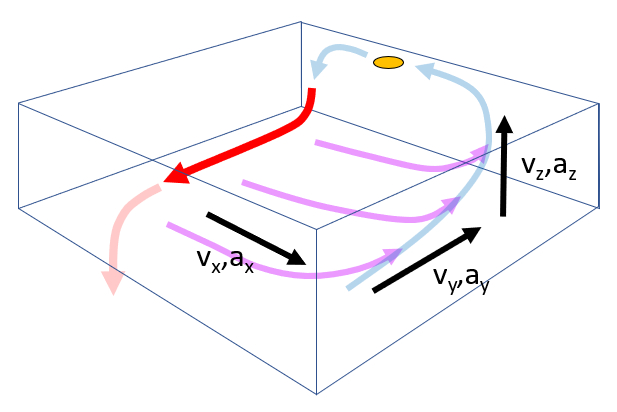
Chaque tape est associ e un temps caract ristique :
- Temps de d placement avec le flux principal $\Delta t_y$
- Temps de d viation avec le flux de perte $\Delta t_x$
- Temps de remont e $\Delta t_z$
Chaque temps caract ristique est associ aux vitesses et aux acc l rations le long du trajet parcouru :
- Avec le flux principal $v_y, a_y$.
- Avec le flux de perte $v_x, a_x$.
- Avec la remont e $v_z, a_z$.
En g n ral, la vitesse initiale (
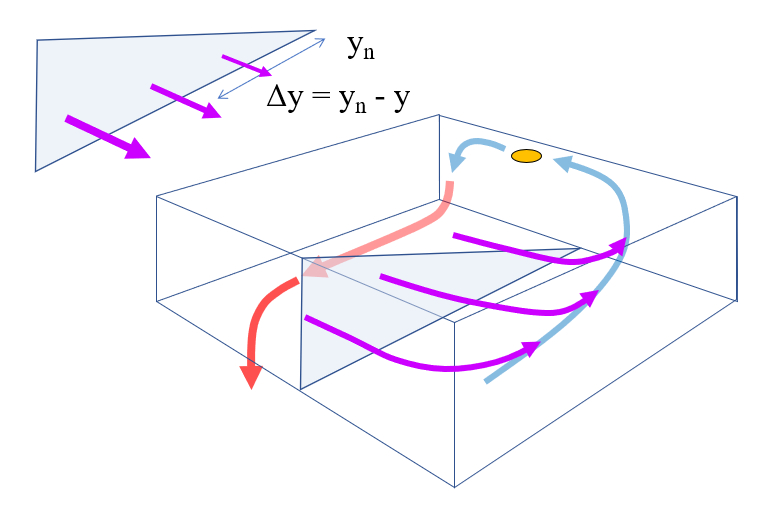
Le flux de perte n\'est pas uniforme et se distribue le long de la latitude, il est donc mod lis en fonction de sa distance par rapport la position la plus au nord. Ainsi, il est nul aux latitudes nord et maximal sur le bord sud du rectangle o la circulation est mod lis e:
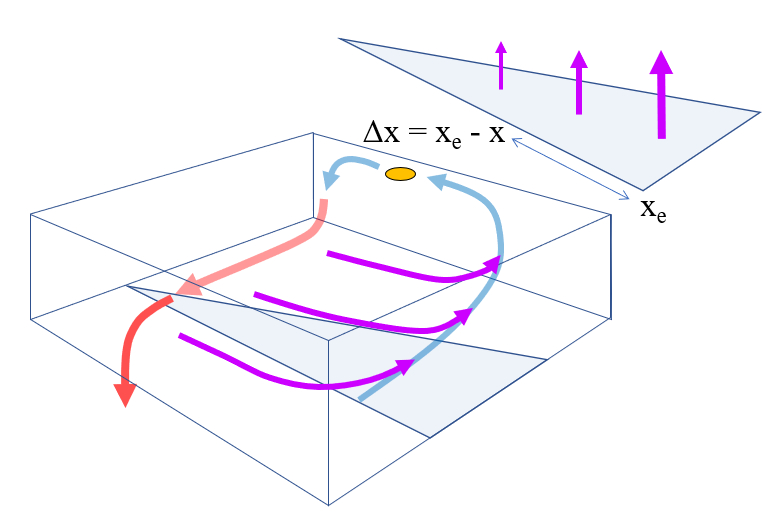
Comme le flux de perte n\'est pas uniforme, il en est de m me pour la surgence. Dans le m me mod le, on suppose qu\'elle est maximale sur le bord est du rectangle o la circulation est mod lis e. De mani re analogue la perte, on suppose une relation lin aire:
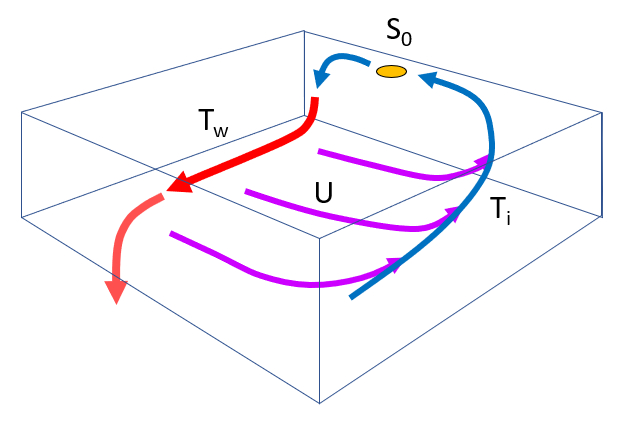
La mod lisation du flux profond n cessite la prise en compte de quatre types de flux :
Le flux principal $F_w$, qui se d place le long du fond marin.
Le flux de perte $F_i$, qui est la fraction d vi e en raison de la force de Coriolis.
Le flux de remont e $U_x$, qui correspond la fraction du flux de perte atteignant la surface.
Le flux de submersion $S_0$, provenant des courants de surface, incluant les pertes qui s\'enfoncent nouveau.
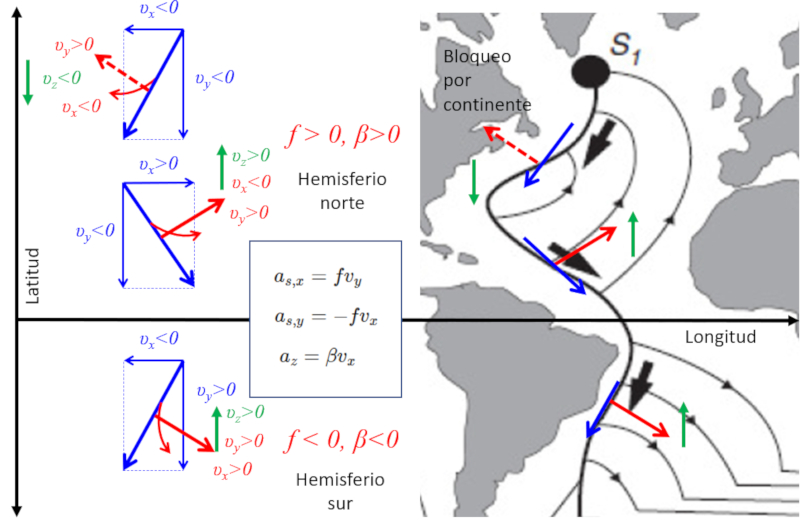
La force de Coriolis, ainsi nomm e, joue un r le essentiel dans la dynamique de l\'eau aux p les en influen ant la descente des masses d\'eau en raison des variations de temp rature et de salinit .
Lors de l\'analyse de l\'oc an Atlantique, on peut observer un mouvement de l\'eau du p le vers l\' quateur, d vi vers l\'ouest. Ce ph nom ne est caus par le retard par rapport la rotation de la plan te, lors de la transition d\'une zone de vitesse plus faible le long de la latitude une zone de vitesse plus lev e. Ce comportement peut tre mod lis l\'aide de l\' quation de Coriolis pour la direction x, donn e par
Dans cette quation, le facteur de Coriolis
Le contour g ographique du continent permet un mouvement dans la direction x (longitude), entra nant une acc l ration dans la direction y (latitude), qui peut tre calcul e l\'aide de
Ce calcul r v le que pr s de l\' quateur, des d placements se produisent qui loignent l\'eau du courant principal, la d pla ant vers le nord. Si l\'on examine l\'acc l ration dans la direction z (profondeur) et que l\'on tient compte du fait que
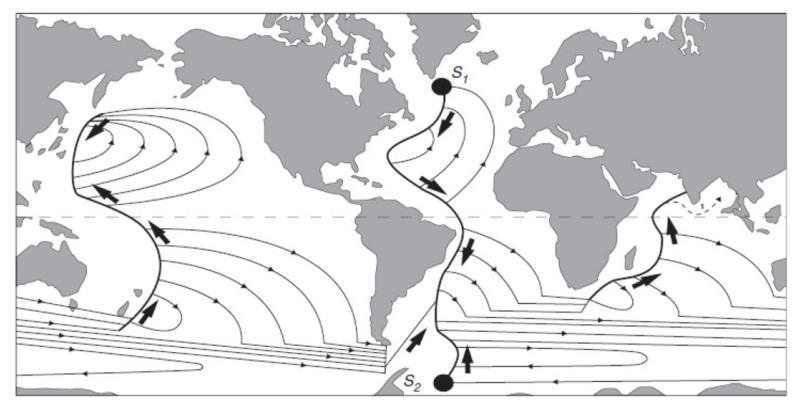
la fin, Stommel et Arons [1], [2] r solvent le mod le en indiquant les principaux flux profonds qui existent travers le globe :
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sur la circulation abyssale de l'oc an mondial - I. Sch mas de flux plan taires stationnaires sur une sph re.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sur la circulation abyssale de l'oc an mondial - II. Un mod le id alis du sch ma et de l'amplitude de la circulation dans les bassins oc aniques.) Deep Sea Research (1953), 6(3), 217-233.
Lorsque Stommel et Arons [1], [2] ont tabli leur premier mod le de circulation thermohaline, ils ont subdivis les diff rents oc ans en zones avec une remont e d'eau d finie (fl ches pointant vers le haut) et deux sources, une dans l'Arctique et l\'autre en Antarctique :
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Sur la circulation abyssale de l'oc an mondial - I. Sch mas de flux plan taires stationnaires sur une sph re.) Deep Sea Research (1953), 6(2), 140-154.
[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Sur la circulation abyssale de l'oc an mondial - II. Un mod le id alis du sch ma et de l'amplitude de la circulation dans les bassins oc aniques.) Deep Sea Research (1953), 6(3), 217-233.
Les mesures ont montr que la circulation thermohaline est un syst me int gr qui couvre l\'ensemble du globe. Il y a au moins deux points qui peuvent tre consid r s comme des sources, et son trajet p n tre tous les oc ans.
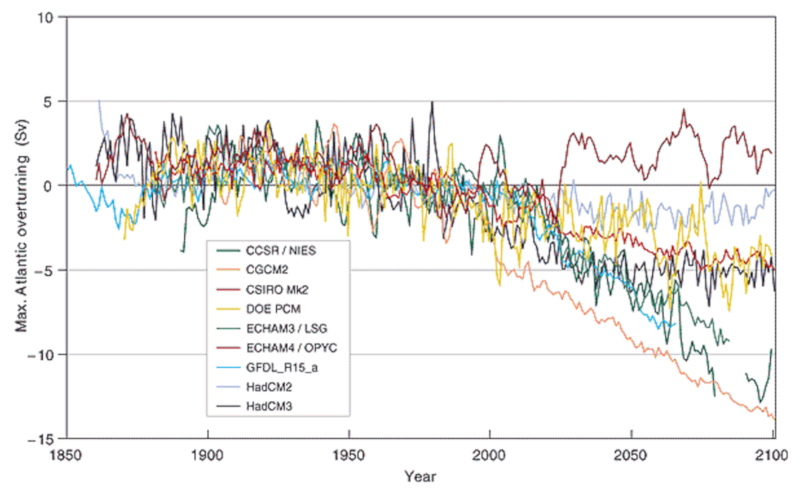
travers de multiples simulations, les effets de la fonte des glaces polaires sur la suppression des enfouissements et son impact sur la circulation profonde sont tudi s. Il existe des indications selon lesquelles la circulation a commenc diminuer. Cependant, l'effondrement de la circulation profonde n\'implique pas n cessairement le m me sc nario pour la circulation de surface, qui est g n r e par les vents. Ce qui pourrait se produire, c\'est un d placement de la circulation de surface, entra nant une r duction de la contribution du courant du Gulf Stream en eau chaude vers le nord de l\'Europe.
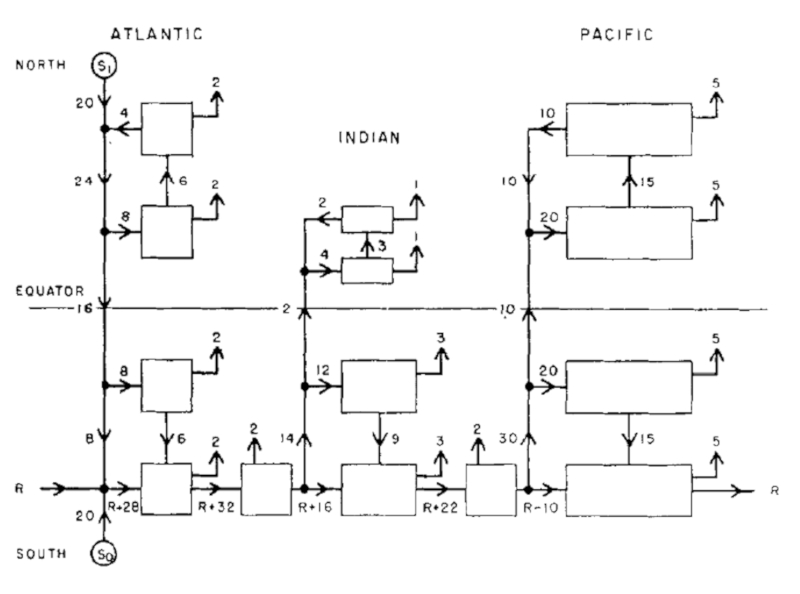
Le diagramme ci-dessous montre les variations des flux en unit s de Sv (Sverdrup), quivalentes $10^6,m^3/s$ :
En supposant un taux d\'enfouissement d\'environ 20 Sv, on peut en conclure que certaines simulations montrent l\'arr t de la circulation profonde. Ces variations sont associ es diff rents sc narios futurs de l\'activit humaine et des consid rations pour des aspects o il y a moins de certitude quant leur occurrence. Des informations plus d taill es peuvent tre consult es dans les rapports du Groupe d\'experts intergouvernemental sur l\' volution du climat (GIEC).
Lors de la mod lisation de l\'Atlantique Nord comme une bo te avec un syst me de coordonn es proche de l\' quateur et dans la r gion des Cara bes, la largeur de la bo te est calcul e en soustrayant la position ouest de la position est:
Lors de la mod lisation de l\'Atlantique Nord comme une bo te avec un syst me de coordonn es proche de l\' quateur et dans la r gion des Cara bes, la hauteur de la bo te est obtenue en soustrayant la position sud de la position nord:
En analogie avec le facteur de Coriolis, nous pouvons tudier comment ce facteur varie le long de l'arc, ce qui nous conduit obtenir le facteur bêta de Coriolis ($\beta$) donn par a latitude ($\varphi$), le rayon de la planète ($R$) et a vitesse angulaire de la planète ($\omega$) par :
En se basant sur la relation entre l'acc l ration de Coriolis et les vitesses dans chaque axe, nous pouvons estimer l'acc l ration de la remont e qui se produira dans la circulation. En utilisant la param trisation qui d pend de la taille du secteur et de la latitude de l'emplacement, nous obtenons a accélération de Coriolis dans la direction z ($a_{c,z}$) en fonction de le facteur bêta de Coriolis ($\beta$), le rayon de la planète ($R$) et a vitesse parallèle ($v_x$) :
Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) peut tre r crit avec le facteur de Coriolis ($f$) et la condition qu'il n'y a pas de mouvement vertical :
$v_z = 0$
il en r sulte que a accélération de Coriolis à la surface, dans la direction x ($a_{c,x}$) est :
Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) peut tre r crit avec le facteur de Coriolis ($f$) et sous la condition qu'il n'y ait pas de mouvement vertical :
$v_z = 0$
Ainsi, on d duit que a accélération de Coriolis à la surface, dans la direction y ($a_{c,y}$) est :
Le mouvement le long d'une latitude, d la rotation de la Terre, g n re une acc l ration de Coriolis a accélération de Coriolis à la surface, dans la direction y ($a_{c,y}$), qui dans le mouvement d'intervalle de temps caractéristique en $y$ ($\Delta t_y$) produit a vitesse en méridien ($v_y$) selon :
La vitesse de remont e a vitesse de remontée ($v_z$) est d termin e par a accélération de Coriolis dans la direction z ($a_{c,z}$) en fonction de le mouvement d'intervalle de temps caractéristique en $z$ ($\Delta t_z$) :
Pour simplifier les quations, nous travaillons avec un facteur de Coriolis ($f$), qui est une constante pour l'emplacement physique, car elle inclut a vitesse angulaire de la planète ($\omega$) pour la Terre et a latitude ($\varphi$) pour l'emplacement :
Dans l'h misph re sud, la latitude est n gative, et avec elle, 8600, ce qui explique pourquoi les syst mes tournent dans le sens oppos l'h misph re nord.
La circulation du flux fait que a vitesse parallèle ($v_x$) tend avoir une magnitude similaire a vitesse en méridien ($v_y$) dans un gyre n gatif :
La continuit du flux nous permet de d terminer comment les vitesses sont li es dans chaque phase. De cette mani re, nous pouvons estimer a vitesse de remontée ($v_z$) en fonction de le facteur bêta de Coriolis ($\beta$), le facteur de Coriolis ($f$), le mouvement d'intervalle de temps caractéristique en $y$ ($\Delta t_y$), le mouvement d'intervalle de temps caractéristique en $z$ ($\Delta t_z$), le rayon de la planète ($R$) et a vitesse en méridien ($v_y$):
Comme la vitesse de surgissement est d termin e par
et la relation entre les temps doit respecter
la vitesse au fond est donn e par
La remont e d pend de la vitesse vers la surface et de la position dans la bo te. tant donn qu\'elle est plus lev e vers l\' quateur et relativement uniforme sur toute la largeur, elle est mod lis e de mani re varier uniquement en fonction de la distance jusqu\'au bord nord de la bo te :
$y_n - y$
Ainsi, avec
La vitesse d\'afflux est d termin e l\'aide de la valeur
Le flux l\'int rieur de la bo te peut tre mod lis l\'aide de l\' quation
Plus pr cis ment, on observe que la vitesse d\'afflux est plus lev e vers le bord ouest, ce qui peut tre repr sent par
avec
La pr sence du facteur 2 dans le mod le tient compte de la prise d\'une moyenne en fonction du gradient existant.
Le temps dans la direction
La conservation du flux implique que le flux qui se d place le long de la c te est de l\'Am rique, repr sent par $T_w$, et les composantes qui subissent un upwelling, repr sent es par $U_x$, sont initialement g n r s par le volume qui s\'enfonce, indiqu par $S_0$, en plus de ceux provenant de la circulation par le biais de l\'upwelling. Par cons quent, nous pouvons l\'exprimer de la mani re suivante:
Dans ce cas, il existe deux types de flux : le flux de surface et le flux vers ou depuis la profondeur. Par conservation, on peut supposer que le flux total qui s\' coule vers les profondeurs au point S_0 doit correspondre au flux total g n r par l\'upwelling. Ce dernier se produit sur toute la surface et avec une vitesse verticale, donc :
Si la vitesse est multipli e par
avec la hauteur
$T_i \sim v_y H \Delta x$
Donc, avec
En consid rant l\' quation de bilan avec
et la contribution de la source avec
ainsi que le flux de fond avec
et l\'upwelling avec
en supposant que la zone atteint l\' quateur (
Puisque le facteur de Coriolis est donn par
il peut tre reli au facteur b ta en fonction de sa variation autour d\'une position. Cela est d au d veloppement de Taylor, o nous obtenons :
$f \sim f_0 + \frac{df}{dy}y$
o la d riv e est :
$\frac{df}{dy} = 2\omega\cos\theta = \beta$
Ainsi, en utilisant
Avec
peut tre r crite comme
en utilisant
ID:(1623, 0)