The Action of the Coriolis Force
Storyboard 
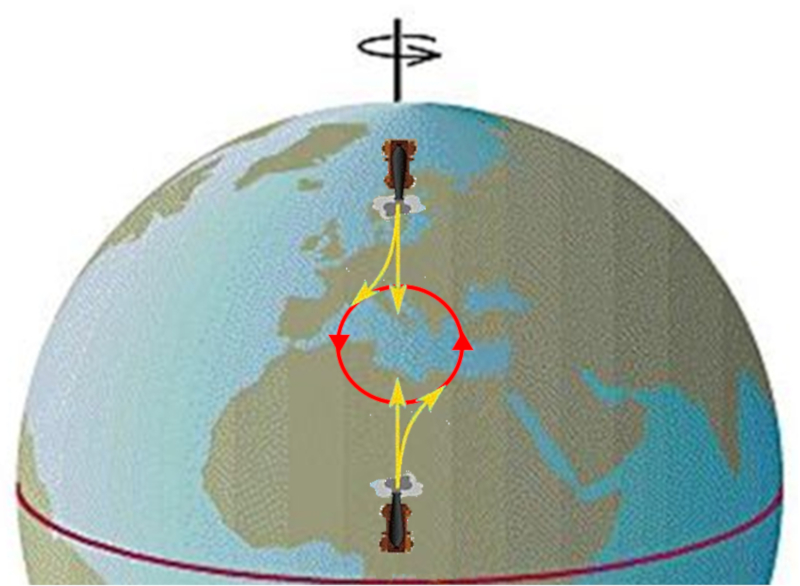
Whenever an object moves in a straight line at a constant speed from a rotating frame of reference (such as the surface of the Earth), it appears to undergo a curved motion. This phenomenon can be modeled by introducing a fictitious force known as the Coriolis force. This force helps us understand various movements observed in the oceans and atmosphere.
ID:(1521, 0)
The Action of the Coriolis Force
Storyboard 
Whenever an object moves in a straight line at a constant speed from a rotating frame of reference (such as the surface of the Earth), it appears to undergo a curved motion. This phenomenon can be modeled by introducing a fictitious force known as the Coriolis force. This force helps us understand various movements observed in the oceans and atmosphere.
Variables
Calculations
Calculations
Equations
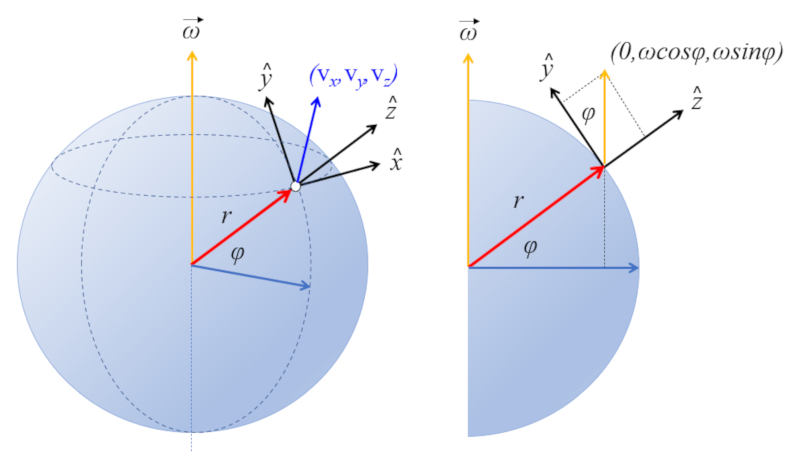
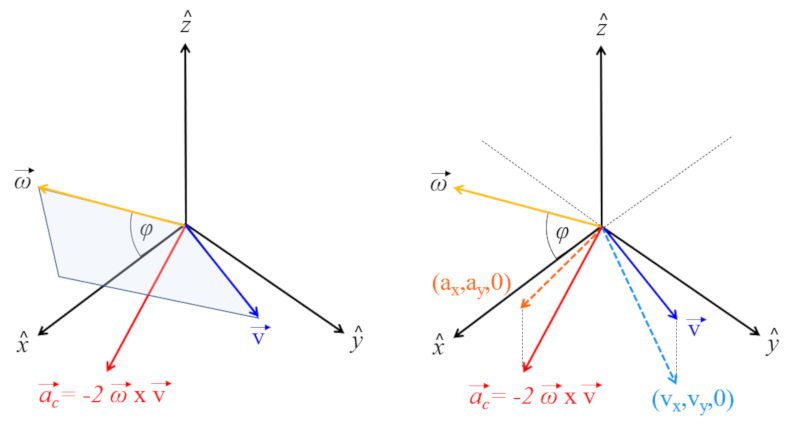
On the Earth's surface, its axis points northward with an angle equal to the latitude ($\varphi$) relative to the plane. Thus, the angular Speed ($\vec{\omega}$) equals:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
And since the body speed ($\vec{v}$) is:
$\vec{v}=(v_x,v_y,v_z)$
the definition of the coriolis acceleration ($\vec{a}_c$):
yields the x-component equal to:
On the Earth's surface, its axis points northward with an angle equal to the latitude ($\varphi$) relative to the plane. Thus, the angular Speed ($\vec{\omega}$) equals:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
And since the body speed ($\vec{v}$) is:
$\vec{v}=(v_x,v_y,v_z)$
the definition of the coriolis acceleration ($\vec{a}_c$):
yields the y-component equal to:
On the Earth's surface, its axis points northward with an angle equal to the latitude ($\varphi$) relative to the plane. Thus, the angular Speed ($\vec{\omega}$) equals:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
And since the body speed ($\vec{v}$) is:
$\vec{v}=(v_x,v_y,v_z)$
the definition of the coriolis acceleration ($\vec{a}_c$):
yields the z-component equal to:
As the coriolis acceleration in x direction ($a_{c,x}$) is composed of the angular velocity of the planet ($\omega$), the latitude ($\varphi$), the speed y of the object ($v_y$), and the speed z of the object ($v_z$):
and the definition of the coriolis factor ($f$) is:
in addition to the constraint of movement on the surface where:
$v_z = 0$
this leads to the coriolis acceleration in x direction ($a_{c,x}$) being:
Since the coriolis acceleration in y direction ($a_{c,y}$) is composed of the angular velocity of the planet ($\omega$), the speed x of the object ($v_x$), and the latitude ($\varphi$):
and the definition of the coriolis factor ($f$) is:
in addition to the constraint of movement on the surface where:
$v_z = 0$
this leads to the coriolis acceleration in y direction ($a_{c,y}$) being:
Since the coriolis acceleration in y direction ($a_{c,y}$) is composed of the angular velocity of the planet ($\omega$), the speed x of the object ($v_x$), and the latitude ($\varphi$):
and the definition of the second Coriolis factor ($e$) is:
in addition to the constraint of movement on the surface where:
$v_z = 0$
this leads to the coriolis acceleration on the surface, in the z direction ($a_{c,z}$) being:
Examples
In the video, we observe how an object appears to follow a curved path when observed from a rotating system. However, from a non-rotating reference frame, its motion appears to be straight and at a constant velocity.
To describe the motion of an object moving rectilinearly in a rotating system, a fictitious force called the Coriolis force is introduced. This force accounts for the observed motion and is essential for understanding various phenomena observed in rotating systems, such as ocean currents and atmospheric circulation patterns.
A local reference system is established where:
• the z-axis points upwards
• the y-axis points northward
• the x-axis points eastward
Thus, the angular velocity vector of the planet lies in the yz plane at an angle equal to the latitude of the location:
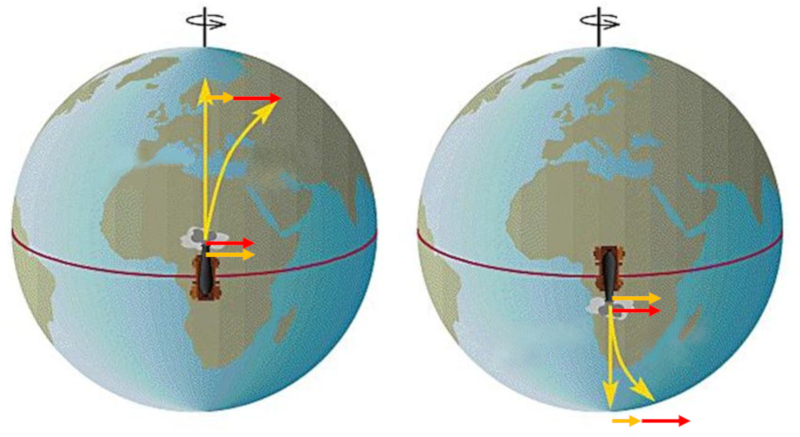
The effect of apparent deviation can be observed particularly on the surface of the Earth. If an object is launched from the equator and travels to higher latitudes, it appears to "advance" due to the fact that at higher latitudes, the tangential velocity is lower than at the equator.
If an object is launched from a location far from the equator towards the east, it will be observed that the body deviates, falling behind, due to its lower tangential velocity compared to latitudes closer to the equator.
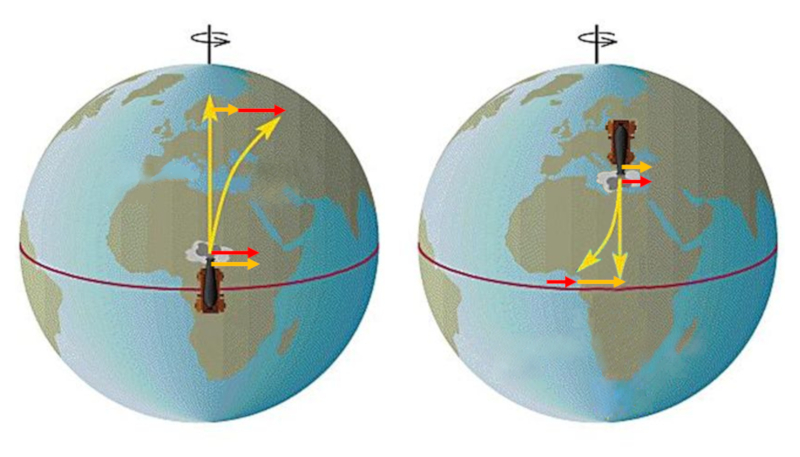
If the flowing medium moves from a point, such as high-pressure air, the flows are delayed or advanced depending on whether they are directed towards the equator or the pole. This leads to the formation of a system that rotates counterclockwise in the northern hemisphere, forming what is known as a cyclone.
If the medium in motion flows towards a point (for example, in the air, from a low-pressure area), the flows are either advanced or delayed depending on whether they come from the equator or the pole. This leads to the formation of a system that rotates in the positive direction (in the northern hemisphere), resulting in what is known as an anticyclone.
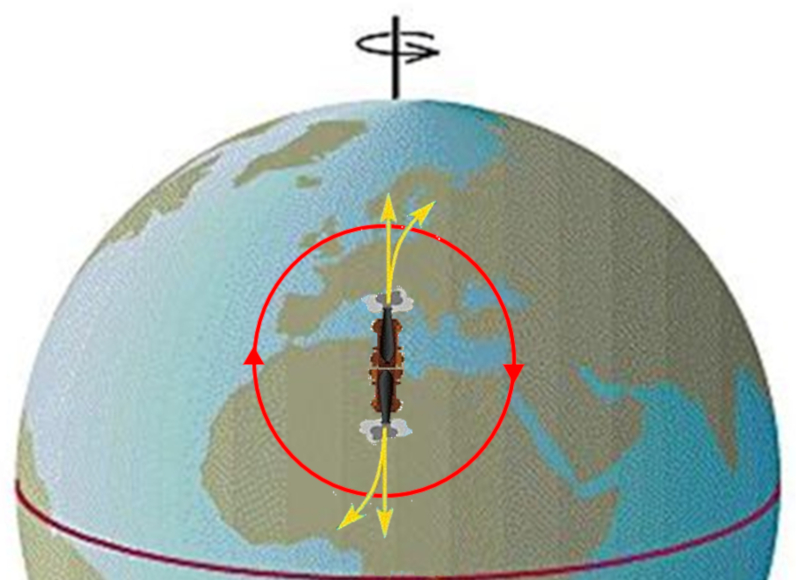
If we only observe what happens in the plane, we will see that whenever we move in a particular direction, we experience a perpendicular acceleration in the positive direction. The magnitude of this acceleration increases with latitude and is zero at the equator. Outside of that, it is proportional to the angular velocity, meaning that if the reference system did not rotate, there would be no Coriolis effect.
The Coriolis acceleration explains how an object deviates from its path due to the rotation of the reference system.
It's important to understand that the 'force,' 'acceleration,' or 'effect' of Coriolis is a mathematical 'trick' to calculate how a body behaves when viewed from a rotating system. The equation that best models this effect is the coriolis acceleration ($\vec{a}_c$) with the angular Speed ($\vec{\omega}$) and the body speed ($\vec{v}$):
The coriolis acceleration ($\vec{a}_c$) is with the angular Speed ($\vec{\omega}$) and the body speed ($\vec{v}$):
So, with the coriolis acceleration in x direction ($a_{c,x}$) alongside the angular velocity of the planet ($\omega$), the speed y of the object ($v_y$), the speed z of the object ($v_z$), and the latitude ($\varphi$), the x-component is.
The coriolis acceleration ($\vec{a}_c$) is related to the angular Speed ($\vec{\omega}$) and the body speed ($\vec{v}$):
So, with the coriolis acceleration in y direction ($a_{c,y}$) alongside the angular velocity of the planet ($\omega$), the speed x of the object ($v_x$), and the latitude ($\varphi$), the y-component is:
The coriolis acceleration ($\vec{a}_c$) is related to the angular Speed ($\vec{\omega}$) and the body speed ($\vec{v}$):
So, with the coriolis acceleration in z direction ($a_{c,z}$) alongside the angular velocity of the planet ($\omega$), the speed x of the object ($v_x$), and the latitude ($\varphi$), the y-component is:
To simplify the equations, we work with ERROR:8600.1, which is a constant for the physical location, as it includes the angular velocity of the planet ($\omega$) for the Earth and the latitude ($\varphi$) for the location:
In the southern hemisphere, the latitude is negative, and with it, 8600, explaining why systems rotate in the opposite direction to the northern hemisphere.
To simplify the equations, we work with ERROR:10273.1, which is a constant for the physical location, as it includes the angular velocity of the planet ($\omega$) for the Earth and the latitude ($\varphi$) for the location:
As the coriolis acceleration in x direction ($a_{c,x}$) can be rewritten with the coriolis factor ($f$) and under the condition that there is no vertical movement:
$v_z = 0$
Therefore, it follows that the coriolis acceleration on the surface, in the x direction ($a_{c,x}$) is:
Since the coriolis acceleration in x direction ($a_{c,x}$) can be rewritten with the coriolis factor ($f$) under the condition that there is no vertical movement:
$v_z = 0$
Then, it follows that the coriolis acceleration on the surface, in the y direction ($a_{c,y}$) is:
Since the coriolis acceleration in z direction ($a_{c,z}$) can be rewritten with the second Coriolis factor ($e$) under the condition that there is no vertical movement:
$v_z = 0$
Then, it follows that the coriolis acceleration on the surface, in the z direction ($a_{c,z}$) is:
ID:(1521, 0)