Die Wirkung der Coriolis-Kraft
Storyboard 
Immer wenn ein Objekt sich in einer geraden Linie mit konstanter Geschwindigkeit aus einem rotierenden Bezugssystem bewegt (wie etwa der Oberfläche der Erde), erscheint es, als ob es eine gekrümmte Bewegung ausführt. Dieses Phänomen kann durch Einführung einer fiktiven Kraft namens Corioliskraft modelliert werden. Diese Kraft hilft uns, verschiedene Bewegungen zu verstehen, die im Ozean und in der Atmosphäre beobachtet werden.
ID:(1521, 0)
Die Wirkung der Coriolis-Kraft
Storyboard 
Immer wenn ein Objekt sich in einer geraden Linie mit konstanter Geschwindigkeit aus einem rotierenden Bezugssystem bewegt (wie etwa der Oberfläche der Erde), erscheint es, als ob es eine gekrümmte Bewegung ausführt. Dieses Phänomen kann durch Einführung einer fiktiven Kraft namens Corioliskraft modelliert werden. Diese Kraft hilft uns, verschiedene Bewegungen zu verstehen, die im Ozean und in der Atmosphäre beobachtet werden.
Variablen
Berechnungen
Berechnungen
Gleichungen
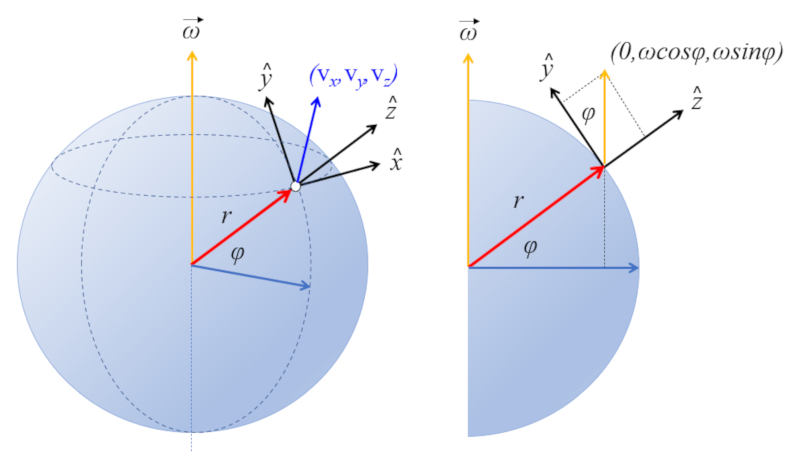
Auf der Erdoberfl che zeigt ihre Achse nach Norden und bildet mit der Ebene einen Winkel von die Breitengrad ($\varphi$). Deshalb ist die Winkelgeschwindigkeit ($\vec{\omega}$) gleich:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
Und da die Körpergeschwindigkeit ($\vec{v}$) lautet:
$\vec{v}=(v_x,v_y,v_z)$
die Definition von die Coriolis-Beschleunigung ($\vec{a}_c$):
ergibt die x-Komponente gleich:
Auf der Erdoberfl che zeigt ihre Achse nach Norden und bildet mit der Ebene einen Winkel von die Breitengrad ($\varphi$). Deshalb ist die Winkelgeschwindigkeit ($\vec{\omega}$) gleich:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
Und da die Körpergeschwindigkeit ($\vec{v}$) lautet:
$\vec{v}=(v_x,v_y,v_z)$
die Definition von die Coriolis-Beschleunigung ($\vec{a}_c$):
ergibt die y-Komponente gleich:
Auf der Erdoberfl che zeigt ihre Achse nach Norden und bildet mit der Ebene einen Winkel von die Breitengrad ($\varphi$). Deshalb ist die Winkelgeschwindigkeit ($\vec{\omega}$) gleich:
$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$
Und da die Körpergeschwindigkeit ($\vec{v}$) lautet:
$\vec{v}=(v_x,v_y,v_z)$
die Definition von die Coriolis-Beschleunigung ($\vec{a}_c$):
ergibt die z-Komponente gleich:
Da die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) aus die Winkelgeschwindigkeit des Planeten ($\omega$), die Breitengrad ($\varphi$), die Geschwindigkeit y des Objekt ($v_y$) und die Geschwindigkeit z des Objekt ($v_z$) besteht:
und die Definition von der Coriolis-Faktor ($f$) lautet:
zus tzlich zur Einschr nkung der Bewegung auf der Oberfl che, wo:
$v_z = 0$
ergibt sich, dass die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) ist:
Da die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) aus die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit x des Objekt ($v_x$) und die Breitengrad ($\varphi$) besteht:
und die Definition von der Coriolis-Faktor ($f$) lautet:
zus tzlich zur Einschr nkung der Bewegung auf der Oberfl che, wo gilt:
$v_z = 0$
f hrt dies dazu, dass die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) folgenderma en ist:
Da die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) aus die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit x des Objekt ($v_x$) und die Breitengrad ($\varphi$) besteht:
und die Definition von der Zweiter Coriolis-Faktor ($e$) lautet:
zus tzlich zur Einschr nkung der Bewegung auf der Oberfl che, wo gilt:
$v_z = 0$
f hrt dies dazu, dass die Coriolis-Beschleunigung an der Oberfläche in z-Richtung ($a_{c,z}$) folgenderma en ist:
Beispiele
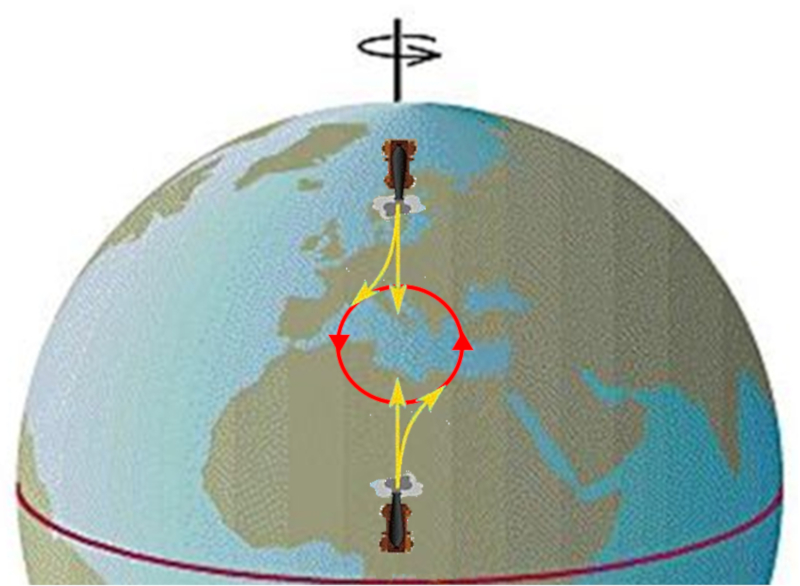
Im Video ist zu beobachten, wie sich ein Objekt scheinbar auf einem gekr mmten Pfad bewegt, wenn es aus einem rotierenden System betrachtet wird. Aus einem nicht rotierenden Bezugssystem erscheint seine Bewegung jedoch geradlinig und mit konstanter Geschwindigkeit.
Um die Bewegung eines Objekts zu beschreiben, das sich in einem rotierenden System geradlinig bewegt, wird ein fiktive Kraft eingef hrt, die als Corioliskraft bezeichnet wird. Diese Kraft erkl rt die beobachtete Bewegung und ist wesentlich f r das Verst ndnis verschiedener Ph nomene, die in rotierenden Systemen auftreten, wie zum Beispiel Meeresstr mungen und atmosph rische Zirkulationsmuster.
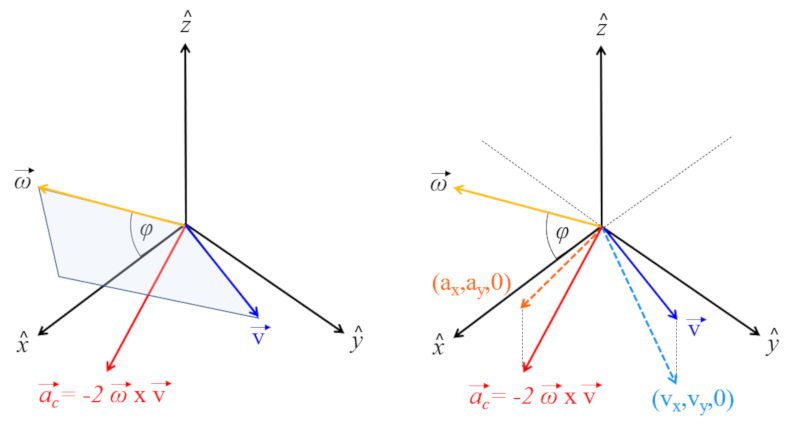
Es wird ein lokales Referenzsystem festgelegt, in dem definiert ist:
• die z-Achse zeigt nach oben
• die y-Achse zeigt nach Norden
• die x-Achse zeigt nach Osten
Daher liegt der Vektor der Winkelgeschwindigkeit des Planeten in der yz-Ebene unter einem Winkel, der der Breite des Ortes entspricht:
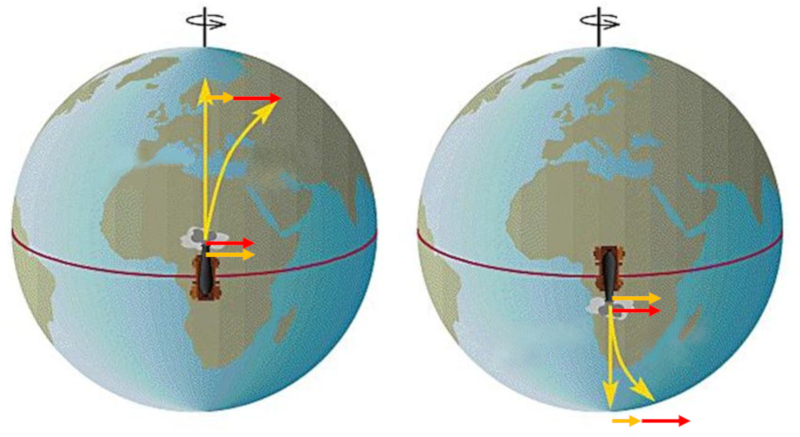
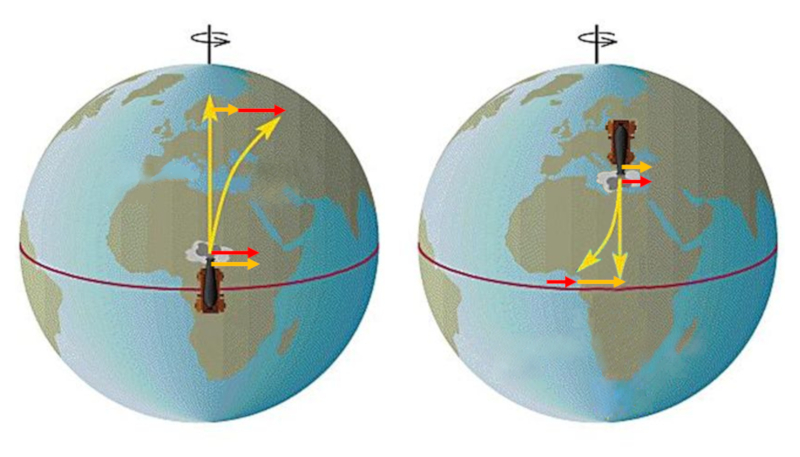
Der Effekt der scheinbaren Abweichung l sst sich besonders gut an der Oberfl che der Erde beobachten. Wenn ein Objekt vom quator aus gestartet wird und in h here Breitengrade vordringt, scheint es sich "vorw rts" zu bewegen, da die Tangentialgeschwindigkeit in h heren Breitengraden geringer ist als am quator.
Wenn ein Objekt von einem Ort weit entfernt vom quator nach Osten gestartet wird, wird beobachtet, dass sich der K rper aufgrund seiner geringeren Tangentialgeschwindigkeit im Vergleich zu Breitengraden in der N he des quators zur ckbleibt.
Wenn sich das str mende Medium von einem Punkt aus bewegt, wie beispielsweise Luft mit hohem Druck, werden die Str mungen verz gert oder beschleunigt, je nachdem, ob sie sich zum quator oder zum Pol hin bewegen. Dies f hrt zur Bildung eines Systems, das sich gegen den Uhrzeigersinn im n rdlichen Hemisph re dreht und das bildet, was als Zyklon bekannt ist.
Wenn das Medium, das sich bewegt, in Richtung eines Punktes str mt (zum Beispiel in der Luft, von einem Tiefdruckgebiet), werden die Str mungen je nachdem, ob sie vom quator oder vom Pol kommen, entweder vorverlegt oder verz gert. Dies f hrt zur Bildung eines Systems, das sich in positiver Richtung dreht (in der Nordhalbkugel), was zu dem f hrt, was als Antizyklon bekannt ist.
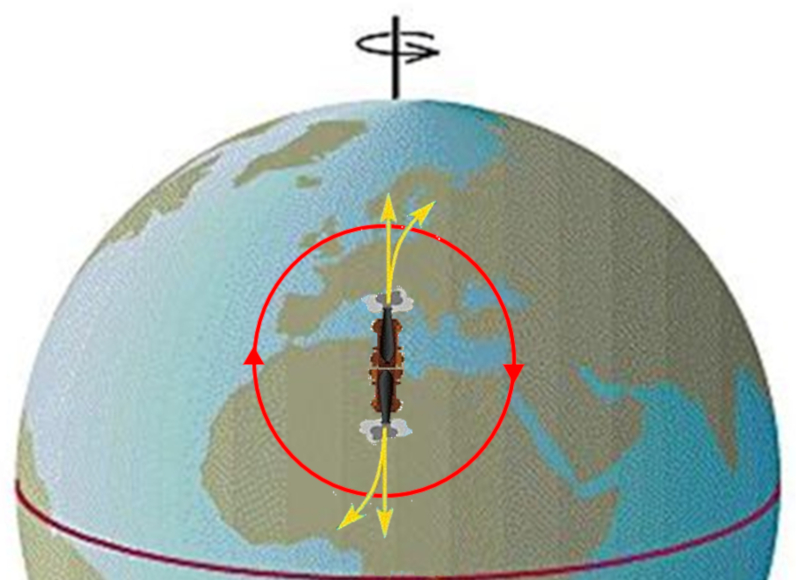
Wenn wir nur das betrachten, was in der Ebene passiert, werden wir feststellen, dass wir jedes Mal, wenn wir uns in eine bestimmte Richtung bewegen, eine senkrechte Beschleunigung in positiver Richtung erfahren. Die Gr e dieser Beschleunigung nimmt mit der Breitengrad zu und ist am quator Null. Au erhalb davon ist sie proportional zur Winkelgeschwindigkeit, was bedeutet, dass es keinen Corioliseffekt g be, wenn sich das Bezugssystem nicht drehen w rde.
Die Coriolis-Beschleunigung erkl rt, wie ein Objekt durch die Rotation des Bezugssystems von seinem Kurs abweicht.
Es ist wichtig zu verstehen, dass die 'Kraft', 'Beschleunigung' oder 'Effekt' von Coriolis ein mathematischer 'Trick' ist, um zu berechnen, wie sich ein K rper verh lt, wenn er aus einem rotierenden System betrachtet wird. Die Gleichung, die diesen Effekt am besten modelliert, ist die Coriolis-Beschleunigung ($\vec{a}_c$) mit die Winkelgeschwindigkeit ($\vec{\omega}$) und die Körpergeschwindigkeit ($\vec{v}$):
Die Coriolis-Beschleunigung ($\vec{a}_c$) ist mit die Winkelgeschwindigkeit ($\vec{\omega}$) und die Körpergeschwindigkeit ($\vec{v}$):
Daher ist mit die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) neben die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit y des Objekt ($v_y$), die Geschwindigkeit z des Objekt ($v_z$) und die Breitengrad ($\varphi$) die x-Komponente.
Die Coriolis-Beschleunigung ($\vec{a}_c$) ist verbunden mit die Winkelgeschwindigkeit ($\vec{\omega}$) und die Körpergeschwindigkeit ($\vec{v}$):
Dann ist mit die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) neben die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit x des Objekt ($v_x$) und die Breitengrad ($\varphi$) die y-Komponente:
Die Coriolis-Beschleunigung ($\vec{a}_c$) ist verbunden mit die Winkelgeschwindigkeit ($\vec{\omega}$) und die Körpergeschwindigkeit ($\vec{v}$):
Dann ist mit die Coriolis-Beschleunigung in z-Richtung ($a_{c,z}$) neben die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit x des Objekt ($v_x$) und die Breitengrad ($\varphi$) die y-Komponente:
Um die Gleichungen zu vereinfachen, arbeiten wir mit ein Coriolis-Faktor ($f$), was eine Konstante f r den physischen Ort ist, da es die Winkelgeschwindigkeit des Planeten ($\omega$) f r die Erde und die Breitengrad ($\varphi$) f r den Ort einschlie t:
Im s dlichen Hemisph re ist die Breitengrade negativ, und damit 8600, was erkl rt, warum Systeme sich in die entgegengesetzte Richtung zum n rdlichen Hemisph re drehen.
Um die Gleichungen zu vereinfachen, arbeiten wir mit ein Zweiter Coriolis-Faktor ($e$), was eine Konstante f r den physischen Ort ist, da es die Winkelgeschwindigkeit des Planeten ($\omega$) f r die Erde und die Breitengrad ($\varphi$) f r den Ort einschlie t:
Da sich die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) mit der Coriolis-Faktor ($f$) umschreiben l sst und unter der Bedingung, dass es keine vertikale Bewegung gibt:
$v_z = 0$
ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in x-Richtung ($a_{c,x}$) lautet:
Da sich die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) unter der Bedingung, dass keine vertikale Bewegung vorhanden ist, mit der Coriolis-Faktor ($f$) umschreiben l sst:
$v_z = 0$
Folglich ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in y-Richtung ($a_{c,y}$) ist:
Da sich die Coriolis-Beschleunigung in z-Richtung ($a_{c,z}$) unter der Bedingung, dass keine vertikale Bewegung vorhanden ist, mit der Zweiter Coriolis-Faktor ($e$) umschreiben l sst:
$v_z = 0$
Folglich ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in z-Richtung ($a_{c,z}$) ist:
ID:(1521, 0)