Ocean movement, drifters
Storyboard 
The movement on the surface of the oceans arises from the interaction with the atmosphere and is conditioned by the deeper currents (more than 15 meters). In a first approximation, it can be considered as a flow at a constant velocity with stable vortices or those dragged by it.
ID:(1519, 0)
Ocean movements
Image 
The movement of the ocean is generated on the surface by the movement of the air while in the depth by variations in density conditioned by temperature and salinity. Different effects are shown in the following NASA video:
ID:(11485, 0)
Gulf stream
Note 
One of the most important currents in the Atlantic Ocean is the so-called Gulf Stream. It carries warm waters from the Caribbean to Europe, contributing to a milder climate in this area:
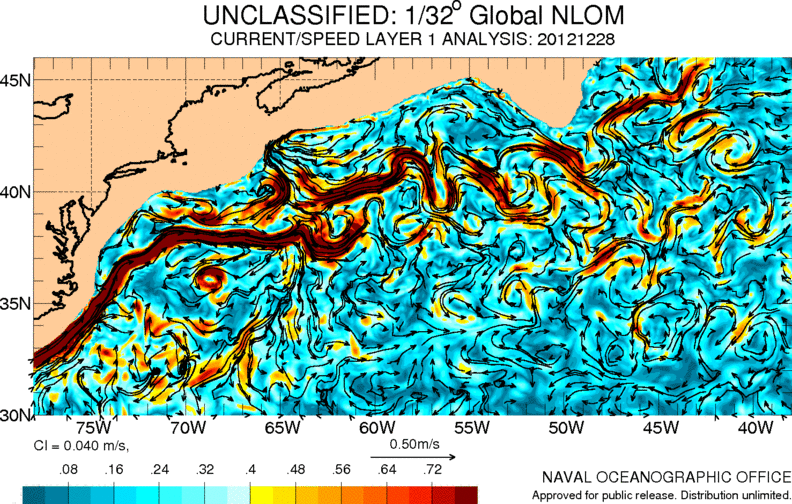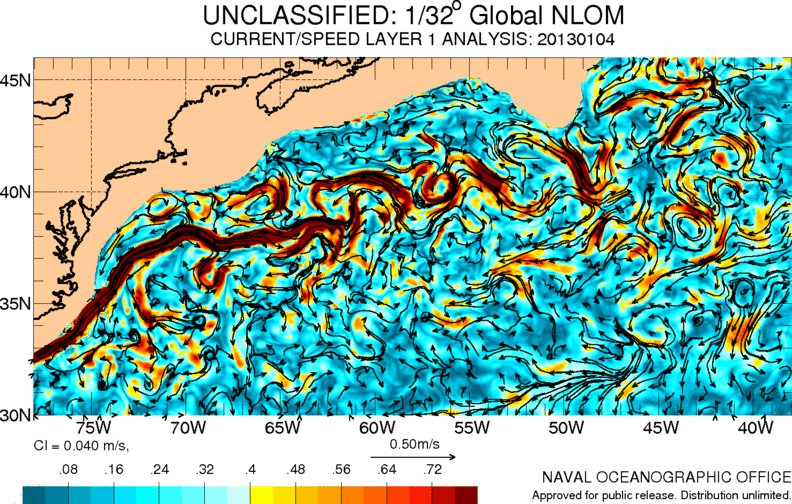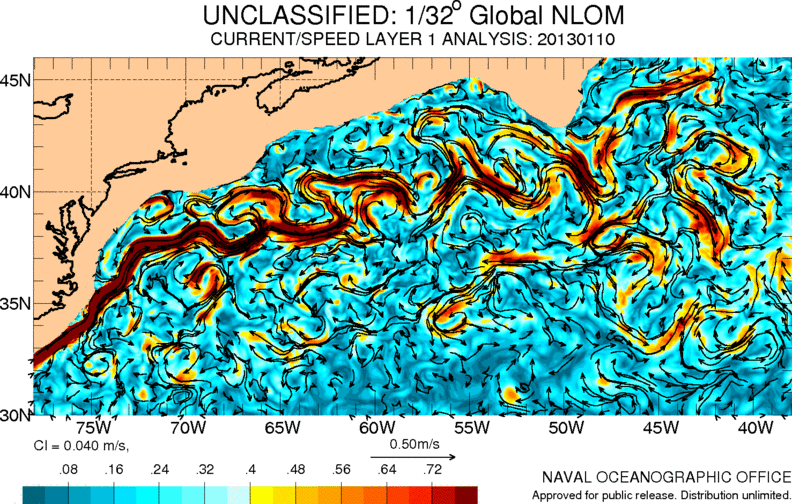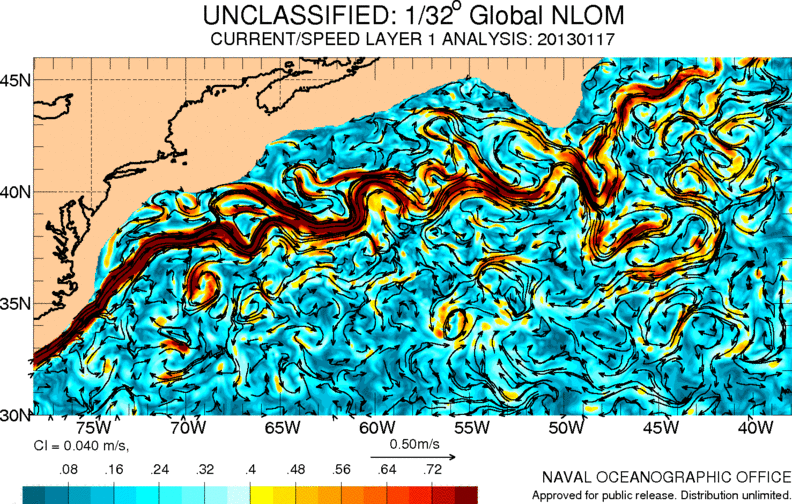
ID:(11486, 0)
Currents in central america and the caribbean
Quote 
The Gulf Stream originates from the Caribbean where there is also a series of circulation associated with the movements of the air masses in the region:
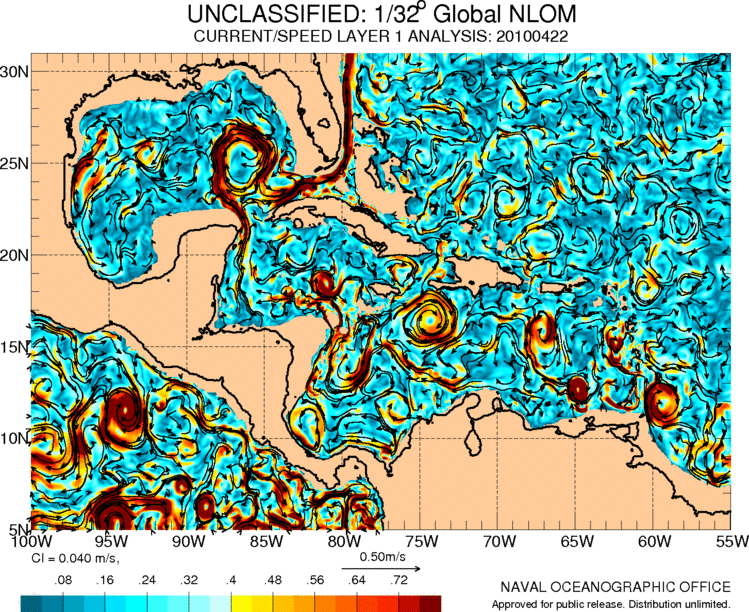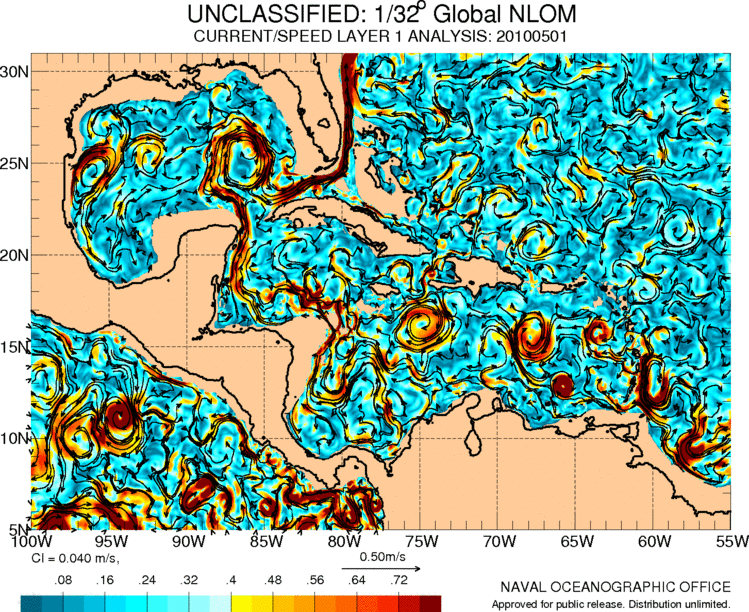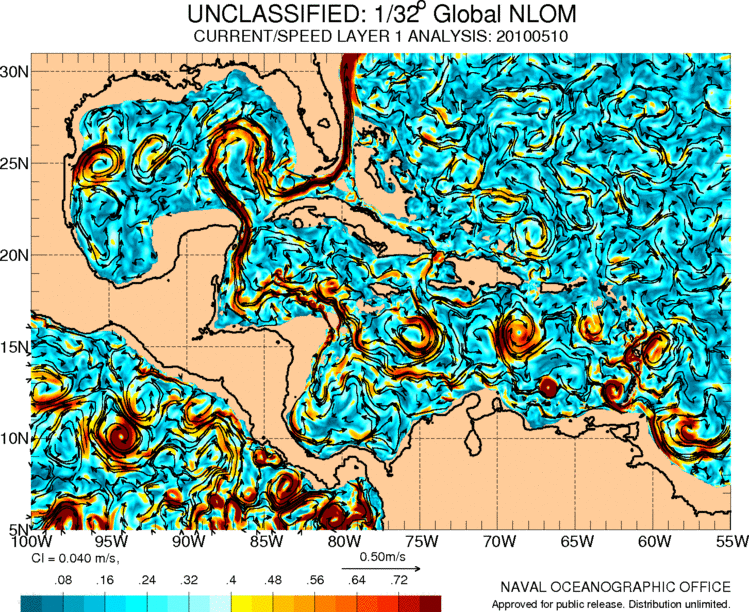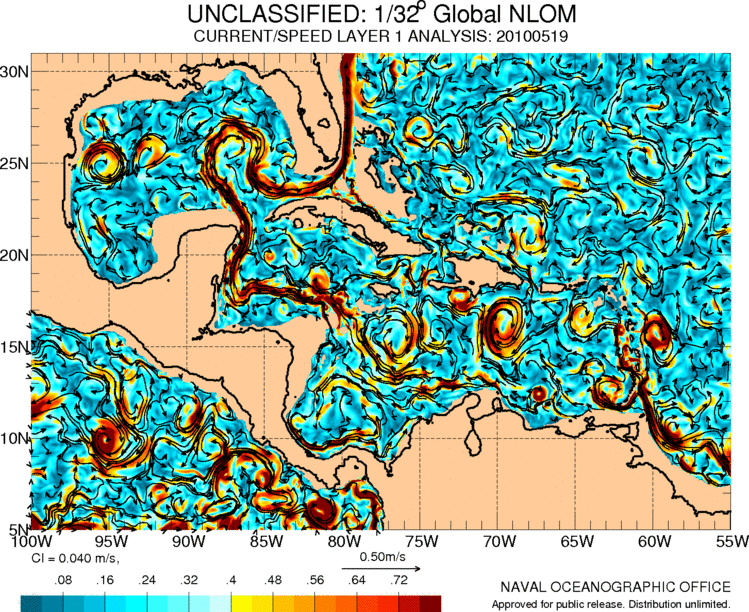
ID:(11487, 0)
X-15 Ben Franklin movement
Exercise 
In 1969 explorer Jacques Piccard's X-15 Ben Franklin submersible was swept away by the Gulf Stream. I float for this at a depth that corresponded to neutral flotation (between 180 to 610 m) and covered 2324 km:
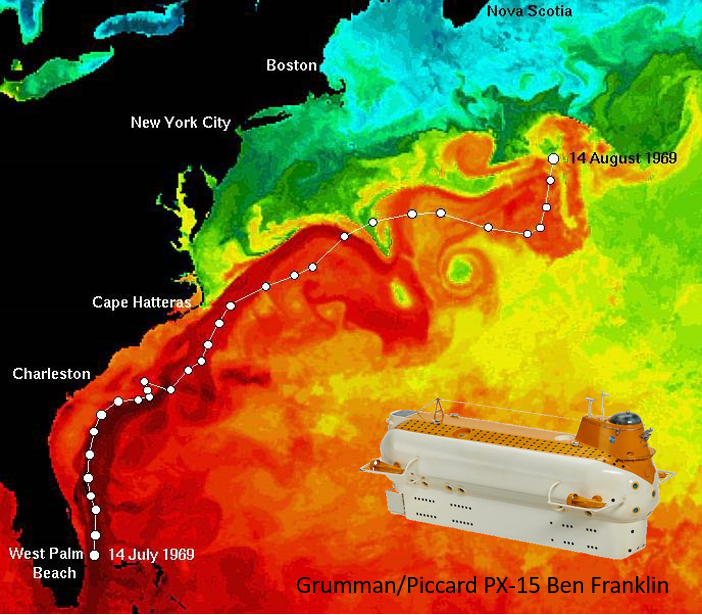
ID:(11488, 0)
Drifter (free buoy)
Equation 
To study ocean currents in the upper layer by measuring position (and with it speed), radiation, temperature and salinity, free buoys are used, which are called langrangian drifters or drifters:
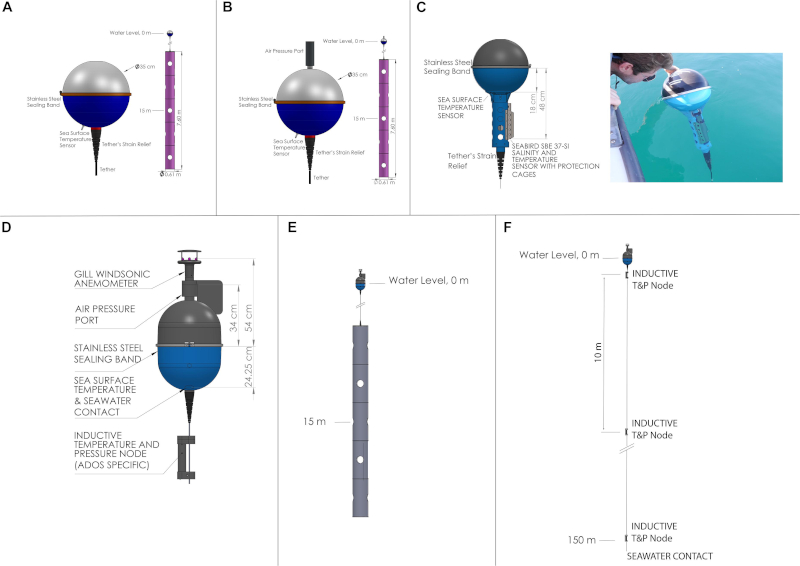
ID:(11498, 0)
Drifters distribution (free buoy)
Script 
There are different programs that have distributed drifers over all the oceans to monitor the flow in the ocean. An example is the Global Drifter Program (GDP) that presents the following distribution:
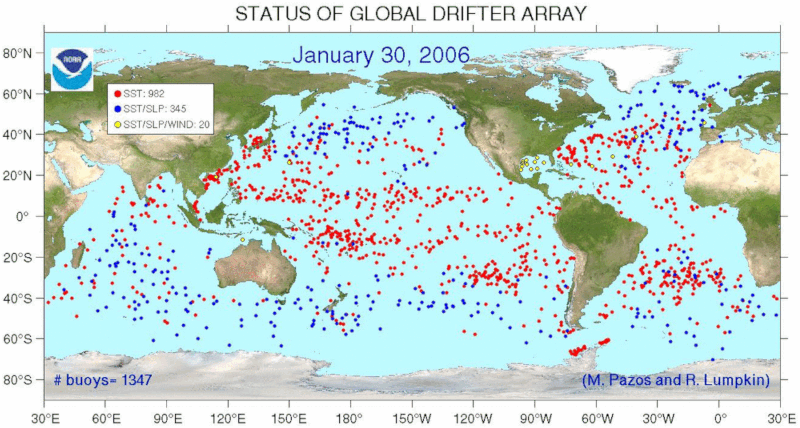
ID:(11499, 0)
Rotation and Traslation, position
Variable 
The rotational movement can be expressed as displacement in the x and y directions with values of the object distance from vortex center ($r$) and the object angle in the vortex ($\theta_w$), respectively. With coordinates the position x of the vortex center ($X$) and the position y of the vortex center ($Y$), we obtain that the position x of the object ($x$) is:
| $ x = X + r \cos \theta_w$ |
and for the position y of the object ($y$):
| $ y = Y + r \sin \theta_w$ |
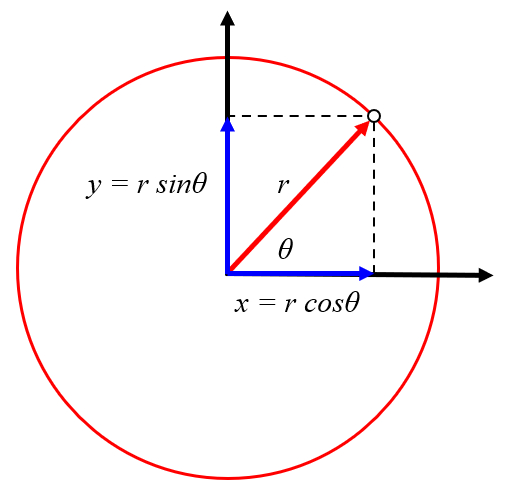
ID:(11490, 0)
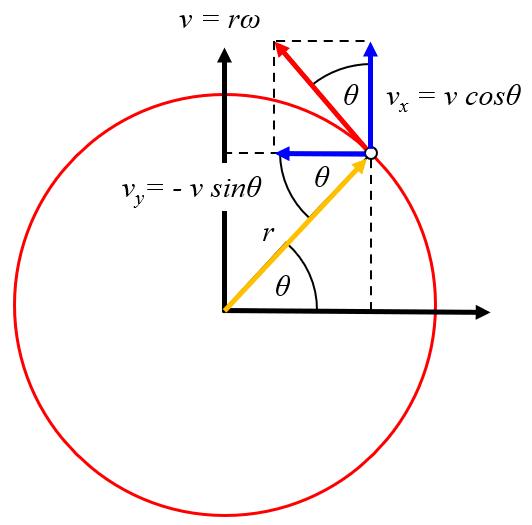
Rotation and Traslation, speed
Audio 
The rotational movement can be expressed as displacement in the x and y directions with velocities of ERROR:9913 and ERROR:9914, respectively. With coordinates the speed x of the vortex center ($U$) and the speed y of the vortex center ($V$), we obtain that ERROR:9913 is:
| $ u = U - r \omega \sin \theta_w $ |
and for ERROR:9914:
| $ v = V + r \omega \cos \theta_w $ |
ID:(11489, 0)
Ocean movement, drifters
Storyboard 
The movement on the surface of the oceans arises from the interaction with the atmosphere and is conditioned by the deeper currents (more than 15 meters). In a first approximation, it can be considered as a flow at a constant velocity with stable vortices or those dragged by it.
Variables
Calculations
Calculations
Equations
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
and the definition of the mean angular velocity ($\bar{\omega}$) is
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
Examples
The movement of the ocean is generated on the surface by the movement of the air while in the depth by variations in density conditioned by temperature and salinity. Different effects are shown in the following NASA video:
One of the most important currents in the Atlantic Ocean is the so-called Gulf Stream. It carries warm waters from the Caribbean to Europe, contributing to a milder climate in this area:
The Gulf Stream originates from the Caribbean where there is also a series of circulation associated with the movements of the air masses in the region:
In 1969 explorer Jacques Piccard's X-15 Ben Franklin submersible was swept away by the Gulf Stream. I float for this at a depth that corresponded to neutral flotation (between 180 to 610 m) and covered 2324 km:
To study ocean currents in the upper layer by measuring position (and with it speed), radiation, temperature and salinity, free buoys are used, which are called langrangian drifters or drifters:
There are different programs that have distributed drifers over all the oceans to monitor the flow in the ocean. An example is the Global Drifter Program (GDP) that presents the following distribution:
The rotational movement can be expressed as displacement in the x and y directions with values of the object distance from vortex center ($r$) and the object angle in the vortex ($\theta_w$), respectively. With coordinates the position x of the vortex center ($X$) and the position y of the vortex center ($Y$), we obtain that the position x of the object ($x$) is:
and for the position y of the object ($y$):
The rotational movement can be expressed as displacement in the x and y directions with velocities of ERROR:9913 and ERROR:9914, respectively. With coordinates the speed x of the vortex center ($U$) and the speed y of the vortex center ($V$), we obtain that ERROR:9913 is:
and for ERROR:9914:
The vortex moves in the $x$ direction with a constant of ERROR:8510.1, from ERROR:8514.1 reaching the time from start of trace ($t$) in $x$ The position x of the vortex center ($X$):
The vortex moves in the $y$ direction with a constant of ERROR:8511.1, from ERROR:8515.1 reaching the time from start of trace ($t$) in $y$ The position y of the vortex center ($Y$):
The vortex rotates steadily at ERROR:8518.1, starting from ERROR:8517.1 and reaching the time from start of trace ($t$) at ERROR:8516.1:
The distance between the object at the position x of the object ($x$) and the position y of the object ($y$) and the center of the vortices at the position x of the vortex center ($X$) and the position y of the vortex center ($Y$) can be calculated using the Pythagorean theorem, resulting in the object distance from vortex center ($r$):
If a body rotates at an angle of the object angle in the vortex ($\theta_w$) at a distance of the object distance from vortex center ($r$) from a center positioned at the position x of the vortex center ($X$), the result is ERROR:8508.1:
If a body rotates at an angle of the object angle in the vortex ($\theta_w$) at a distance of the object distance from vortex center ($r$) from a center located at position the position y of the vortex center ($Y$), the result will be ERROR:8509.1:
If we divide the relationship between the distance traveled in a time ($\Delta s$) and the radius ($r$) by the angle variation ($\Delta\theta$),
and then divide it by the time elapsed ($\Delta t$), we obtain the relationship that allows us to calculate the speed ($v$) along the orbit, known as the tangential velocity, which is associated with the angular Speed ($\omega$):
Since the vortex rotates at the angular velocity of the object in the vortex ($\omega$) and is located ERROR:8519.1 from its center, the object moves at ERROR:10336.1:
If a body is at ERROR:8516.1 and the velocity in the $x$ direction is the speed x of the vortex center ($U$), then ERROR:9913 is:
Given that the vortex rotates at the angular velocity of the object in the vortex ($\omega$) and is located ERROR:8519.1 from its center, the object moves at ERROR:10336.1:
If a body is at ERROR:8516.1 and the velocity in the $y$ direction is the speed y of the vortex center ($V$), then ERROR:9914 is:
ID:(1519, 0)
