Radiación solar
Storyboard 
El origen del clima es el sol. Su energía alcanza a la tierra calentando en forma distinta atmósfera y superficie creando gradientes que son balanceados por conducción, convección y vientos.
Por ello se debe estudiar la potencia del sol, como esta alcanza la tierra y como se distribuye sobre la superficie terrestre.
ID:(534, 0)
El sol
Imagen 
La fuente de energía que determina el clima en la Tierra es el sol.

El Sol (con algunas manchas solares)
Los parámetros clave del sol son los siguientes:
| Parámetro | Variable | Valor |
| Radio | $R$ | 696342 km |
| Superficie | $S$ | 6.09E+12 km2 |
| Masa | $M$ | 1.98855E+30 kg |
| Densidad | $\rho$ | 1.408 g/cm3 |
| Temperatura (superficie) | $T_s$ | 5778 K |
| Potencia | $P$ | 3.846E+26 W |
| Intensidad | $I$ | 6.24E+7 W/m2 |
ID:(3078, 0)
Planeta tierra
Nota 
El planeta Tierra, que se observa en la siguiente imagen:

tiene las siguientes características:
| Parámetro | Símbolo | Valor |
| Distancia al sol | $r$ | 1.496E+8 km |
| Radio | $R$ | 6371.0 km |
| Masa | $M$ | 5.972E+24 kg |
| Periodo de órbita | $T_o$ | 365 días |
| Periodo de rotación | $T_r$ | 24 horas |
| Excentricidad | $\epsilon$ | 0.017 |
| Inclinación del eje | $\phi$ | 23.44° |
ID:(9990, 0)
Los planetas
Cita 
A continuación se muestran las imágenes de los distintos planetas, en orden: Mercurio, Venus, Tierra, Marte, Júpiter, Saturno, Urano, Neptuno y Plutón:

Los diferentes planetas tienen una variedad de radios, masas, periodos de órbita y rotación, inclinación del eje y distancias al sol, que se resumen a continuación:
| Planeta | Radio* | Masa* | Distancia al sol* | Periodo de órbita* | Periodo de rotación* | Excentricidad | Inclinación del eje |
| Mercurio | 0.382 | 0.06 | 0.39 | 0.24 | 58.64 | 0.206 | 0.04° |
| Venus | 0.949 | 0.82 | 0.72 | 0.62 | -243.02 | 0.007 | 177.36° |
| Tierra | 1.000 | 1.00 | 1.00 | 1.00 | 1.00 | 0.017 | 23.44° |
| Marte | 0.532 | 0.11 | 1.52 | 1.88 | 1.03 | 0.093 | 25.19° |
| Júpiter | 11.209 | 317.8 | 5.2 | 11.86 | 0.41 | 0.048 | 3.13° |
| Saturno | 9.449 | 95.2 | 9.54 | 29.46 | 0.43 | 0.054 | 26.73° |
| Urano | 4.007 | 14.6 | 19.22 | 84.01 | -0.72 | 0.047 | 97.77° |
| Neptuno | 3.883 | 17.2 | 30.06 | 164.8 | 0.67 | 0.0009 | 28.32° |
| Plutón | 0.186 | 0.0022 | 39.482 | 247.94 | 1.005 | 0.2488 | 17.16° |
* dato en proporción con el valor para la Tierra
ID:(9991, 0)
Intensidad en la superficie del sol
Ejercicio 
La intensidad de radiación en superficie del sol ($I_s$) se define como la potencia del sol ($P_s$) por unidad de la superficie del sol ($S_s$), donde la potencia se representa por:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
Si modelamos el sol como una esfera de el radio solar ($R_s$), su superficie es:
| $ S_s = 4 \pi R_s ^2$ |
y, por lo tanto, la intensidad de radiación en superficie del sol ($I_s$) se calcula como:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
ID:(15655, 0)
Intensidad del sol en la órbita
Ecuación 
La intensidad a la distancia de la órbita ($I_r$) se define como la potencia del sol ($P_s$) por unidad de la superficie de esfera en la órbita ($S_r$):
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
Si consideramos una esfera imaginaria con un radio igual a la distancia entre el sol y la Tierra, ERROR:10360,0, podemos calcular su sección transversal:
| $ S_r = 4 \pi r ^2$ |
Esto nos permite obtener la intensidad a la distancia de la órbita ($I_r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
ID:(15657, 0)
Radio de la órbita de la tierra y del sol
Script 
La radiación del Sol se propaga a través de su superficie, que tiene un área de $4\pi R_s^2$ donde un radio solar ($R_s$) es el radio del Sol, y se distribuye a la distancia de la órbita de la Tierra, que tiene una superficie igual a $4\pi r^2$ donde una distancia planeta sol ($r$) es la distancia entre la Tierra y el Sol:
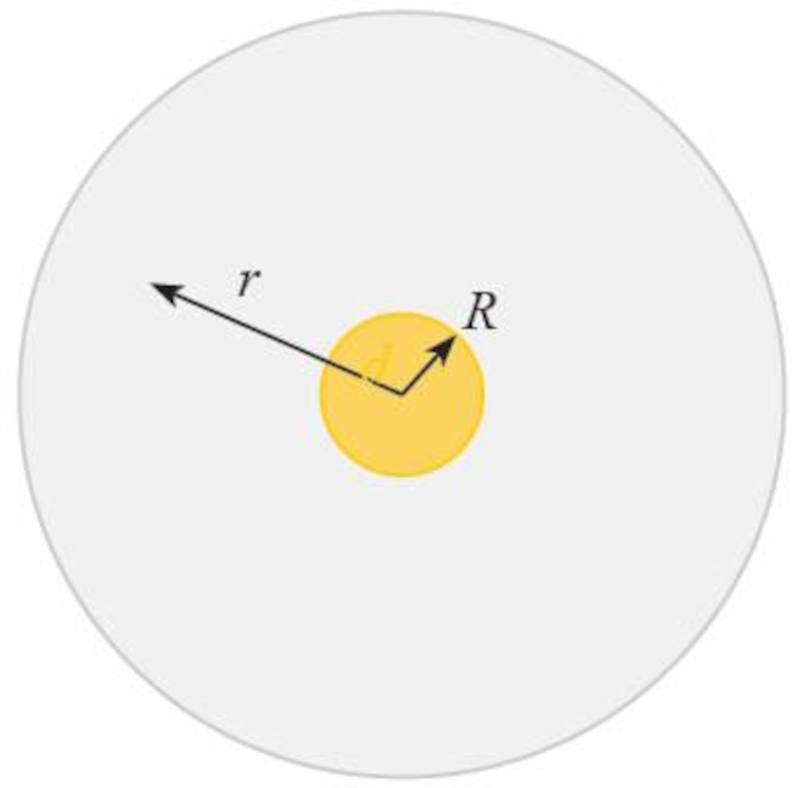
Distribución de la radiación solar
ID:(3082, 0)
Intensidad en orbita con relación al sol
Variable 
Si reemplazamos la potencia del sol ($P_s$) del sol, calculada como la intensidad de radiación en superficie del sol ($I_s$) en la superficie de una esfera con radio ERROR:6492,0:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
,
en la ecuación de la intensidad a la distancia de la órbita ($I_r$) para la luz solar a la distancia planeta sol ($r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
,
podemos obtener la relación entre intensidades:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
ID:(15658, 0)
Potencia capturada por la tierra
Audio 
Dado que la intensidad a la distancia de la órbita ($I_r$) que llega a la Tierra es igual a la potencia captada por el planeta ($P_d$) captada por la sección que presenta el planeta ($S_d$) según:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
y siendo la sección que presenta el planeta ($S_d$) el área del disco de el radio del planeta ($R_p$) igual a:
| $ S_d = \pi R_p ^2$ |
tenemos que:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
.
ID:(15659, 0)
Área en la tierra que captura radiación
Video 
La intensidad media de la tierra ($I_p$) sobre toda la superficie de el radio del planeta ($R_p$) es igual a la intensidad a la distancia de la órbita ($I_r$) captada por un disco de el radio del planeta ($R_p$), por lo que:
$4\pi R_p^2 I_s = \pi R_p^2 I_p$
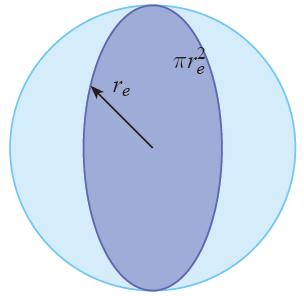
Disco que captura radiación solar
Por lo tanto, se tiene que:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
ID:(3084, 0)
Radiación solar
Descripción 
El origen del clima es el sol. Su energía alcanza a la tierra calentando en forma distinta atmósfera y superficie creando gradientes que son balanceados por conducción, convección y vientos. Por ello se debe estudiar la potencia del sol, como esta alcanza la tierra y como se distribuye sobre la superficie terrestre.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3804)
La intensidad ($I$) se define como la potencia ($P$) por unidad de la superficie de una esfera ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
Si consideramos una esfera imaginaria con ERROR:6490,0, podemos calcular su superficie:
| $ S = 4 \pi r ^2$ |
Esto nos permite obtener la intensidad ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
La intensidad ($I$) se define como la potencia ($P$) por unidad de la superficie de una esfera ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
Si consideramos una esfera imaginaria con ERROR:6490,0, podemos calcular su superficie:
| $ S = 4 \pi r ^2$ |
Esto nos permite obtener la intensidad ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
La intensidad ($I$) se define como la potencia ($P$) por unidad de la superficie de una esfera ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
Si consideramos una esfera imaginaria con ERROR:6490,0, podemos calcular su superficie:
| $ S = 4 \pi r ^2$ |
Esto nos permite obtener la intensidad ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
Si reemplazamos la potencia del sol ($P_s$) del sol, calculada como la intensidad de radiación en superficie del sol ($I_s$) en la superficie de una esfera con radio ERROR:6492,0:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
en la ecuaci n de la intensidad a la distancia de la órbita ($I_r$) para la luz solar a la distancia planeta sol ($r$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
podemos obtener la relaci n entre intensidades:
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
(ID 4663)
(ID 4665)
(ID 4665)
(ID 4665)
Dado que la intensidad ($I$) es la potencia ($P$) captada por la superficie de una esfera ($S$) seg n:
| $ I =\displaystyle\frac{ P }{ S }$ |
y siendo la superficie de un disco ($S$) el rea del disco de el radio de un disco ($r$), que es igual a:
| $ S_d = \pi R_p ^2$ |
,
tenemos que:
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
.
(ID 4666)
Ejemplos
(ID 15660)
La fuente de energ a que determina el clima en la Tierra es el sol.

El Sol (con algunas manchas solares)
Los par metros clave del sol son los siguientes:
| Par metro | Variable | Valor |
| Radio | $R$ | 696342 km |
| Superficie | $S$ | 6.09E+12 km2 |
| Masa | $M$ | 1.98855E+30 kg |
| Densidad | $\rho$ | 1.408 g/cm3 |
| Temperatura (superficie) | $T_s$ | 5778 K |
| Potencia | $P$ | 3.846E+26 W |
| Intensidad | $I$ | 6.24E+7 W/m2 |
(ID 3078)
El planeta Tierra, que se observa en la siguiente imagen:

tiene las siguientes caracter sticas:
| Par metro | S mbolo | Valor |
| Distancia al sol | $r$ | 1.496E+8 km |
| Radio | $R$ | 6371.0 km |
| Masa | $M$ | 5.972E+24 kg |
| Periodo de rbita | $T_o$ | 365 d as |
| Periodo de rotaci n | $T_r$ | 24 horas |
| Excentricidad | $\epsilon$ | 0.017 |
| Inclinaci n del eje | $\phi$ | 23.44 |
(ID 9990)
A continuaci n se muestran las im genes de los distintos planetas, en orden: Mercurio, Venus, Tierra, Marte, J piter, Saturno, Urano, Neptuno y Plut n:

Los diferentes planetas tienen una variedad de radios, masas, periodos de rbita y rotaci n, inclinaci n del eje y distancias al sol, que se resumen a continuaci n:
| Planeta | Radio* | Masa* | Distancia al sol* | Periodo de rbita* | Periodo de rotaci n* | Excentricidad | Inclinaci n del eje |
| Mercurio | 0.382 | 0.06 | 0.39 | 0.24 | 58.64 | 0.206 | 0.04 |
| Venus | 0.949 | 0.82 | 0.72 | 0.62 | -243.02 | 0.007 | 177.36 |
| Tierra | 1.000 | 1.00 | 1.00 | 1.00 | 1.00 | 0.017 | 23.44 |
| Marte | 0.532 | 0.11 | 1.52 | 1.88 | 1.03 | 0.093 | 25.19 |
| J piter | 11.209 | 317.8 | 5.2 | 11.86 | 0.41 | 0.048 | 3.13 |
| Saturno | 9.449 | 95.2 | 9.54 | 29.46 | 0.43 | 0.054 | 26.73 |
| Urano | 4.007 | 14.6 | 19.22 | 84.01 | -0.72 | 0.047 | 97.77 |
| Neptuno | 3.883 | 17.2 | 30.06 | 164.8 | 0.67 | 0.0009 | 28.32 |
| Plut n | 0.186 | 0.0022 | 39.482 | 247.94 | 1.005 | 0.2488 | 17.16 |
* dato en proporci n con el valor para la Tierra
(ID 9991)
La intensidad de radiación en superficie del sol ($I_s$) se define como la potencia del sol ($P_s$) por unidad de la superficie del sol ($S_s$), donde la potencia se representa por:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
Si modelamos el sol como una esfera de el radio solar ($R_s$), su superficie es:
| $ S_s = 4 \pi R_s ^2$ |
y, por lo tanto, la intensidad de radiación en superficie del sol ($I_s$) se calcula como:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
(ID 15655)
La intensidad a la distancia de la órbita ($I_r$) se define como la potencia del sol ($P_s$) por unidad de la superficie de esfera en la órbita ($S_r$):
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
Si consideramos una esfera imaginaria con un radio igual a la distancia entre el sol y la Tierra, ERROR:10360,0, podemos calcular su secci n transversal:
| $ S_r = 4 \pi r ^2$ |
Esto nos permite obtener la intensidad a la distancia de la órbita ($I_r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
(ID 15657)
La radiaci n del Sol se propaga a trav s de su superficie, que tiene un rea de $4\pi R_s^2$ donde un radio solar ($R_s$) es el radio del Sol, y se distribuye a la distancia de la rbita de la Tierra, que tiene una superficie igual a $4\pi r^2$ donde una distancia planeta sol ($r$) es la distancia entre la Tierra y el Sol:

Distribuci n de la radiaci n solar
(ID 3082)
Si reemplazamos la potencia del sol ($P_s$) del sol, calculada como la intensidad de radiación en superficie del sol ($I_s$) en la superficie de una esfera con radio ERROR:6492,0:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
,
en la ecuaci n de la intensidad a la distancia de la órbita ($I_r$) para la luz solar a la distancia planeta sol ($r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
,
podemos obtener la relaci n entre intensidades:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
(ID 15658)
Dado que la intensidad a la distancia de la órbita ($I_r$) que llega a la Tierra es igual a la potencia captada por el planeta ($P_d$) captada por la sección que presenta el planeta ($S_d$) seg n:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
y siendo la sección que presenta el planeta ($S_d$) el rea del disco de el radio del planeta ($R_p$) igual a:
| $ S_d = \pi R_p ^2$ |
tenemos que:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
.
(ID 15659)
La intensidad media de la tierra ($I_p$) sobre toda la superficie de el radio del planeta ($R_p$) es igual a la intensidad a la distancia de la órbita ($I_r$) captada por un disco de el radio del planeta ($R_p$), por lo que:
$4\pi R_p^2 I_s = \pi R_p^2 I_p$

Disco que captura radiaci n solar
Por lo tanto, se tiene que:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
(ID 3084)
(ID 15671)
La intensidad ($I$) se define como la cantidad de la potencia ($P$) irradiada por unidad de la superficie de una esfera ($S$). Por lo tanto, se establece la siguiente relaci n:
| $ I =\displaystyle\frac{ P }{ S }$ |
(ID 9988)
La intensidad ($I$) se define como la cantidad de la potencia ($P$) irradiada por unidad de la superficie de una esfera ($S$). Por lo tanto, se establece la siguiente relaci n:
| $ I =\displaystyle\frac{ P }{ S }$ |
(ID 9988)
La intensidad ($I$) se define como la cantidad de la potencia ($P$) irradiada por unidad de la superficie de una esfera ($S$). Por lo tanto, se establece la siguiente relaci n:
| $ I =\displaystyle\frac{ P }{ S }$ |
(ID 9988)
La intensidad ($I$) se define como la cantidad de la potencia ($P$) irradiada por unidad de la superficie de una esfera ($S$). Por lo tanto, se establece la siguiente relaci n:
| $ I =\displaystyle\frac{ P }{ S }$ |
(ID 9988)
La superficie de una esfera ($S$) de un radio de una esfera ($r$) se puede calcular utilizando la siguiente f rmula:
| $ S = 4 \pi r ^2$ |
(ID 4665)
La superficie de una esfera ($S$) de un radio de una esfera ($r$) se puede calcular utilizando la siguiente f rmula:
| $ S = 4 \pi r ^2$ |
(ID 4665)
La superficie de una esfera ($S$) de un radio de una esfera ($r$) se puede calcular utilizando la siguiente f rmula:
| $ S = 4 \pi r ^2$ |
(ID 4665)
La intensidad ($I$) se calcula como la potencia ($P$) dividido por la superficie de una esfera con un radio ($r$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
La intensidad ($I$) se calcula como la potencia ($P$) dividido por la superficie de una esfera con un radio ($r$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
La intensidad ($I$) se calcula como la potencia ($P$) dividido por la superficie de una esfera con un radio ($r$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
(ID 4662)
La superficie de un disco ($S$) de un radio de un disco ($r$) se calcula de la siguiente manera:
| $ S = \pi r ^2$ |
(ID 3804)
La intensidad ($I$) se calcula dividiendo la potencia ($P$) por el rea del disco de radio el radio ($r$), es decir:
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
(ID 4666)
La proporci n entre la intensidad a la distancia de la órbita ($I_r$) y la intensidad de radiación en superficie del sol ($I_s$) es igual a la proporci n entre la superficie de una esfera de radio el radio solar ($R_s$) y la superficie de una esfera de radio la distancia planeta sol ($r$), por lo que es:
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
(ID 4663)
La intensidad media de la tierra ($I_p$) es igual a un cuarto de la intensidad a la distancia de la órbita ($I_r$) debido a que la superficie de la esfera emisora es cuatro veces mayor que la del disco captador de la radiaci n. Por lo tanto:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
(ID 4667)
ID:(534, 0)
