Usuario:


Equilibrio
Storyboard

En un estado de equilibrio la energía capturada del sol tiene que necesariamente ser igual a aquella que la propia tierra emite devuelta al espacio. La primera llega principalmente como radiación visible, calienta el planeta y este a su vez re emite como radiación infrarroja via la atmósfera devuelta al espacio.

>Modelo

ID:(537, 0)


Modelo de balance de radiación (D1+0)
Imagen

Los flujos de radiación visibles y infrarrojos se han estimado y representan flujos medios sobre toda la superficie del planeta. En este sentido no diferencia lugares sobre el planeta y en ese sentido es un modelo que solo diferencia situaciones según altura en la atmósfera y por ello es unidimensional. Los valores que se han medido se representan en la siguiente gráfica:

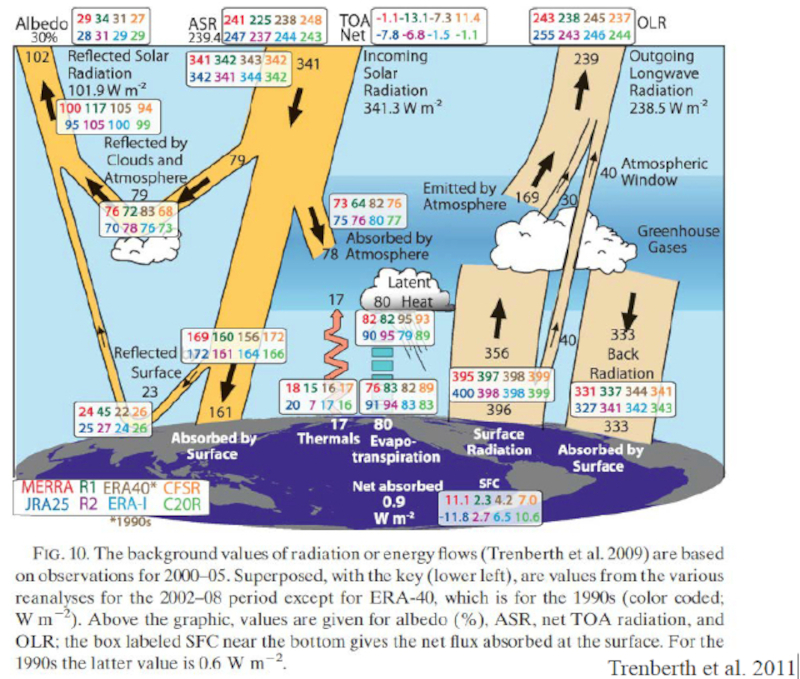
Balance de radiación para un modelo D1+0 según mediciones hechas por distintas instituciones.

En primera aproximación se puede asumir que la superficie del planeta es homogénea, es decir los albedos y coberturas son constantes sobre la superficie. Dentro de este esquema se tiene un modelo unidimensional (1D) en que solo se estudia en mayor detalle el comportamiento de la atmósfera con los parámetros:Datos | Símbolo | Valor | Error | Unidades:--------|:----------:|--------:|:-------:|:-------Coberturas | | | | |Visible | $\gamma_v$ | 0.4377 | 0.0088 | -Infrarrojo | $\gamma_i$ | 0.9069 | 0.0069 | -Albedos | | | | | Atmósfera | $a_a$ | 0.4968 | 0.0066 | -Tierra | $a_e$ | 0.1415 | 0.0114 | -Temperaturas | | | | | Tierra | $T_e$ | 15.16 | - | CAtmósfera inferior (b-bottom) | $T_b$ | 3.75 | - | CAtmósfera superior (t-top) | $T_t$ | -28.13 | - | CFactores | | | | |Factor por calor latente | $\kappa_l$ | 10.6406 | 0.1699 | J/m^3sFactor por convección | $\kappa_c$ | 0.1706 | 0.0136 | J/m^3sKViento en la superficie | $u$ | 8.5 | - | m/s

ID:(3077, 0)


Equilibrio termodinámico
Condición

En general el calor fluye desde los objetos de mayor temperatura a los de menor evolucionando asi las temperaturas de todos los elementos involucrados.Si uno espera un tiempo suficiente los sistemas alcanzan un equilibrio térmico, es decir cada cuerpo esta recibiendo la misma cantidad de calor como entrega a su entrono. En esta situación las temperaturas permanecen constantes en el tiempo y se habla de que el sistema esta en equilibrio termodinámico.

ID:(9976, 0)


Solución numérica
Php

Las ecuaciones de balance radiativo

$(1- a_e )(1- \gamma_v ) I_s -( \kappa_l + \kappa_c ( T_e - T_b )) u - \sigma \epsilon T_e ^4+ \sigma \epsilon T_b ^4=0$



$( \kappa_l + \kappa_c ( T_e - T_b )) u -2 \sigma \epsilon T_b ^4+ \sigma \epsilon T_t ^4+(1- \gamma_i ) \sigma \epsilon T_e ^4=0$



$(1- a_a ) \gamma_v I_s + \sigma \epsilon T_b ^4-2 \sigma \epsilon T_t ^4=0$



nos permiten calcular las temperaturas sobre la superficie de la tierra T_e, en la parte inferior de la atmósfera T_b y en la parte superior T_t.

Para ello la tercera ecuación en T_t y T_b puede ser despejada en la primera variable y reemplazada en la segunda ecuación. De esta forma se obtienen dos ecuaciones en T_e y T_b que de graficarse representan dos superficies que cumplen las ecuaciones en el plano que la tercera dimensión es nula simultaneamente, definiendo las soluciones en ambas temperaturas..

sim=94

ID:(6866, 0)


Equilibrio
Modelo

En un estado de equilibrio la energía capturada del sol tiene que necesariamente ser igual a aquella que la propia tierra emite devuelta al espacio. La primera llega principalmente como radiación visible, calienta el planeta y este a su vez re emite como radiación infrarroja via la atmósfera devuelta al espacio.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$a_a$
a_a
Albedo de la atmósfera de la tierra
-
$a_e$
a_e
Albedo de la superficie del planeta
-
$\gamma_i$
g_i
Cobertura de atmósfera para infrarroja (NIR)
-
$\gamma_v$
g_v
Cobertura de atmósfera para radiación VIS
-
$\kappa_l$
k_l
Coeficiente de calor latente
J/m^3
$\kappa_c$
k_c
Coeficiente de convección
J/m^3K
$\sigma$
s
Constante de Stefan Boltzmann
J/m^2K^4s
$\epsilon$
e
Emisividad
-
$I_d$
I_d
Energía transmitido por conducción y evaporación
W/m^2
$I_p$
I_p
Intensidad media de la tierra
W/m^2
$I_b$
I_b
Intensidad NIR emitida por la parte inferior de la atmósfera
W/m^2
$I_t$
I_t
Intensidad NIR emitida por la parte superior de la atmósfera
W/m^2
$I_e$
I_e
Intensidad NIR emitida por la tierra
W/m^2
$I_{esa}$
I_esa
Intensidad NIR emitida por la tierra a la atmósfera
W/m^2
$I_{sa}$
I_sa
Intensidad VIS absorbida por la atmósfera
W/m^2
$I_{ev}$
I_ev
Intensidad VIS absorbida por la tierra
W/m^2
$T_b$
T_b
Temperatura de la parte inferior de la atmósfera
K
$T_t$
T_t
Temperatura de la parte superior de la atmósfera
K
$T_e$
T_e
Temperatura de la superficie de la tierra
K
$u$
u
Velocidad del viento
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Los flujos de radiaci n visibles y infrarrojos se han estimado y representan flujos medios sobre toda la superficie del planeta. En este sentido no diferencia lugares sobre el planeta y en ese sentido es un modelo que solo diferencia situaciones seg n altura en la atm sfera y por ello es unidimensional. Los valores que se han medido se representan en la siguiente gr fica:

Balance de radiaci n para un modelo D1+0 seg n mediciones hechas por distintas instituciones.

En primera aproximaci n se puede asumir que la superficie del planeta es homog nea, es decir los albedos y coberturas son constantes sobre la superficie. Dentro de este esquema se tiene un modelo unidimensional (1D) en que solo se estudia en mayor detalle el comportamiento de la atm sfera con los par metros:Datos | S mbolo | Valor | Error | Unidades:--------|:----------:|--------:|:-------:|:-------Coberturas | | | | |Visible | $\gamma_v$ | 0.4377 | 0.0088 | -Infrarrojo | $\gamma_i$ | 0.9069 | 0.0069 | -Albedos | | | | | Atm sfera | $a_a$ | 0.4968 | 0.0066 | -Tierra | $a_e$ | 0.1415 | 0.0114 | -Temperaturas | | | | | Tierra | $T_e$ | 15.16 | - | CAtm sfera inferior (b-bottom) | $T_b$ | 3.75 | - | CAtm sfera superior (t-top) | $T_t$ | -28.13 | - | CFactores | | | | |Factor por calor latente | $\kappa_l$ | 10.6406 | 0.1699 | J/m^3sFactor por convecci n | $\kappa_c$ | 0.1706 | 0.0136 | J/m^3sKViento en la superficie | $u$ | 8.5 | - | m/s

(ID 3077)

En general el calor fluye desde los objetos de mayor temperatura a los de menor evolucionando asi las temperaturas de todos los elementos involucrados.Si uno espera un tiempo suficiente los sistemas alcanzan un equilibrio t rmico, es decir cada cuerpo esta recibiendo la misma cantidad de calor como entrega a su entrono. En esta situaci n las temperaturas permanecen constantes en el tiempo y se habla de que el sistema esta en equilibrio termodin mico.

(ID 9976)

Las ecuaciones de balance radiativo

$(1- a_e )(1- \gamma_v ) I_s -( \kappa_l + \kappa_c ( T_e - T_b )) u - \sigma \epsilon T_e ^4+ \sigma \epsilon T_b ^4=0$



$( \kappa_l + \kappa_c ( T_e - T_b )) u -2 \sigma \epsilon T_b ^4+ \sigma \epsilon T_t ^4+(1- \gamma_i ) \sigma \epsilon T_e ^4=0$



$(1- a_a ) \gamma_v I_s + \sigma \epsilon T_b ^4-2 \sigma \epsilon T_t ^4=0$



nos permiten calcular las temperaturas sobre la superficie de la tierra T_e, en la parte inferior de la atm sfera T_b y en la parte superior T_t.

Para ello la tercera ecuaci n en T_t y T_b puede ser despejada en la primera variable y reemplazada en la segunda ecuaci n. De esta forma se obtienen dos ecuaciones en T_e y T_b que de graficarse representan dos superficies que cumplen las ecuaciones en el plano que la tercera dimensi n es nula simultaneamente, definiendo las soluciones en ambas temperaturas..

sim=94

(ID 6866)

ID:(537, 0)