Processos de mistura em águas rasas
Storyboard 
Os mecanismos de mistura em áreas rasas são gerados por diversos tipos de ondas. Entre eles estão as ondas internas, as ondas superficiais, a interação entre ondas e correntes, as marés e a quebra das ondas na costa.
ID:(1629, 0)
Número de Strouhal em função do número de Reynold
Imagem 
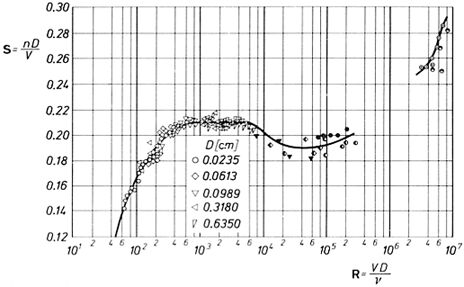
O número de Strouhal ($St$) está relacionado empiricamente com o número de Reynolds ($Re$). O número de Strouhal ($St$) está associado com la frequência de geração de vórtice ($\omega$), la velocidade de fricção ($U_d$) e la profundidade total ($H$) é
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
Isso permite estimar, através de o número de Reynolds ($Re$), a frequência com que a concentração pode trocar os componentes a serem difundidos. No entanto, deve-se ter em mente que o processo pode ser interrompido se a frequência for menor do que a das marés.
ID:(12199, 0)
Estresse cinemático
Descrição 
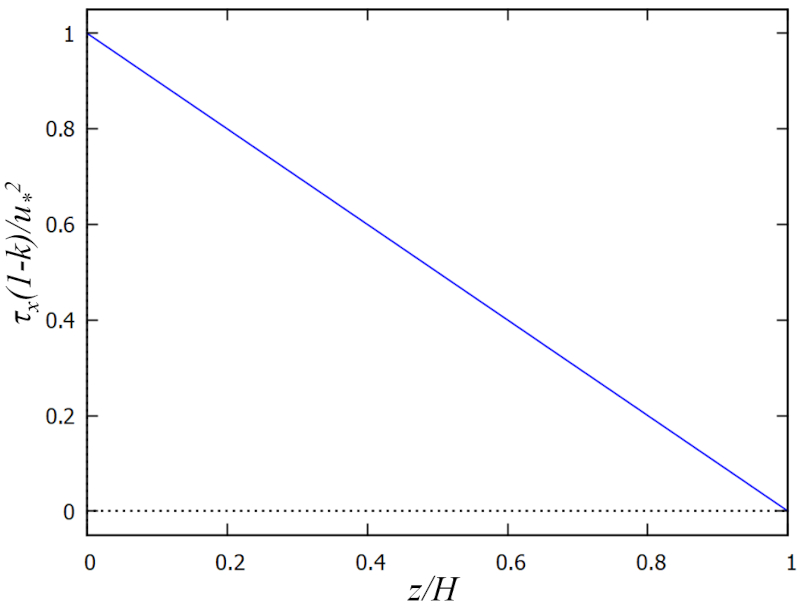
Se assumirmos que não há vento na superfície, pode-se supor que não há tensão na superfície. Portanto, haverá apenas a tensão da água no fundo. Esta tensão diminuirá linearmente do fundo para a superfície. Para simplificar a modelagem, pode-se usar a proporção entre la profundidade ($z$) e la profundidade total ($H$), o que nos dá um fator adimensional la profundidade relativa ($\xi$). La estresse cinemático ($\tau_x$) será, portanto, proporcional a
$\tau_x \propto 1-\xi$
Como la estresse cinemático ($\tau_x$) é equivalente à densidade de energia dividida pela densidade, o valor no fundo deve ser proporcional ao quadrado da velocidade no fundo. Isso é descrito no modelo com la velocidade de fricção ($U_d$) e significa que
$\tau_x \propto U_d^2$
Finalmente, há o efeito de la rugosidade ($k$) do fundo do mar, ou seja, a proporção de o desigualdade ($d$) e la profundidade total ($H$). Isso significa que la estresse cinemático ($\tau_x$) deve ser corrigido por um fator análogo à profundidade:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Assim, obtém-se um modelo da seguinte forma:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
que é representado graficamente a seguir:
ID:(15630, 0)
Comprimento de mistura
Descrição 
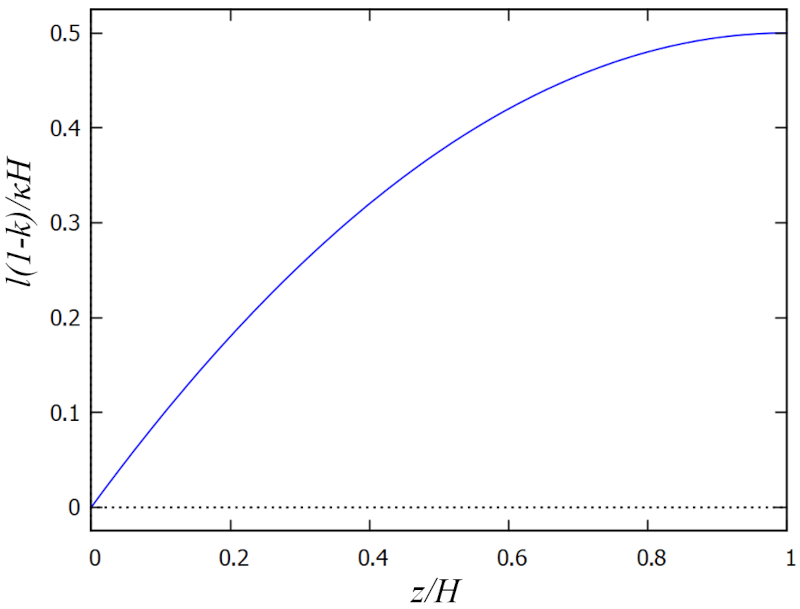
La comprimento de mistura ($l$) corresponde ao que poderia ser descrito como o tamanho dos vórtices. Próximo à parede, esses vórtices só podem ter um tamanho máximo igual à distância até a parede, que é mínima. À medida que nos aproximamos da superfície, esses vórtices podem se tornar cada vez maiores, então a função deve atingir um máximo nesse ponto.
Para simplificar a modelagem, pode-se usar a proporção entre la profundidade ($z$) e la profundidade total ($H$), o que nos proporciona um fator adimensional la profundidade relativa ($\xi$). Assim, uma função simples que atende a essa descrição é:
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
Por outro lado, o modelo de camada limite de Prandtl mostra que estas são uma fração do fluxo com uma largura igual a la profundidade total ($H$) e uma proporção de la constante de Karman ($\kappa$), então:
$l \propto \kappa H$
Finalmente, devemos corrigir pelo efeito da rugosidade da mesma forma que para o estresse cinemático:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Portanto, la comprimento de mistura ($l$) pode ser modelado da seguinte forma:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
ID:(12201, 0)
Viscosidade do redemoinho
Conceito 
Quando Prandtl modela a formação de turbilhões perto das paredes, ele estabelece a relação entre la viscosidade turbulenta ($A$), la comprimento de mistura ($l$) e o gradiente de o perfil da velocidade ($u_z$) em la profundidade ($z$) da seguinte forma:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
Por outro lado, a força viscosa típica, que é modelada como a viscosidade multiplicada pela superfície de contato e o gradiente de velocidade, corresponde a la estresse cinemático ($\tau_x$) no caso das turbulências:
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
De ambas as equações, surge a relação:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Essa relação permite calcular la viscosidade turbulenta ($A$) em função de la estresse cinemático ($\tau_x$) e la comprimento de mistura ($l$), que são modelados neste caso. Assim, com la profundidade total ($H$), la velocidade de fricção ($U_d$), la rugosidade ($k$), la profundidade relativa ($\xi$) e la constante de Karman ($\kappa$):
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
que é representado a seguir:
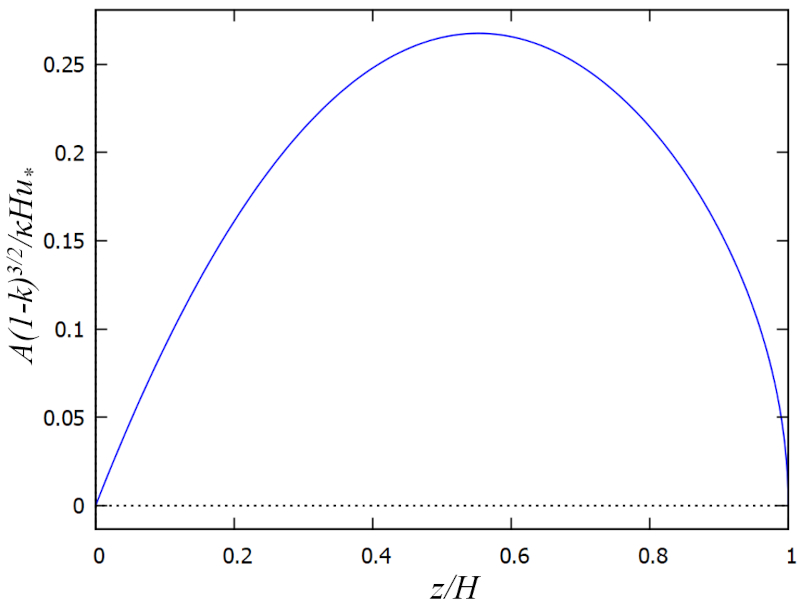
O resultado é que a viscosidade turbulenta é máxima na profundidade média e se reduz a valores mínimos tanto próximo ao fundo quanto próximo à superfície. Ou seja, nessas zonas a mistura e a perda de momento são menores.
ID:(15624, 0)
Perfil de velocidade
Conceito 
Como la estresse cinemático ($\tau_x$) é igual a la viscosidade turbulenta ($A$) e ao gradiente de o perfil da velocidade ($u_z$) em la profundidade ($z$), a equação pode ser integrada para obter o perfil de velocidade:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} , dz'$
Após integrar essa expressão, com la velocidade de fricção ($U_d$), la constante de Karman ($\kappa$), la rugosidade ($k$) e la profundidade relativa ($\xi$), obtemos:
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
que corresponde à famosa lei logarítmica desenvolvida por Prandtl e Schlichting.
O perfil é mostrado no seguinte gráfico:
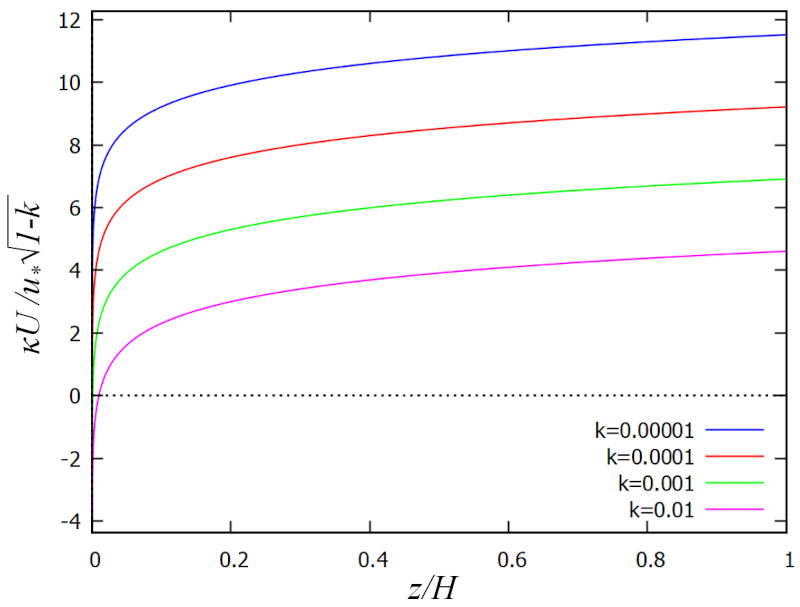
O perfil também permite relacionar tanto ERROR:9467 com la velocidade de fricção ($U_d$) em função de la rugosidade ($k$) e la constante de Karman ($\kappa$), o que, por sua vez, permite definir um ERROR:9468 com:
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
e
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
ID:(15623, 0)
Concentração de sedimentos
Conceito 
Se considerarmos o comportamento do material suspenso, observamos dois principais fatores. Primeiramente, há uma tendência de que ele se sedimente com uma velocidade la taxa de sedimentação ($\omega_s$), gerando um fluxo que depende de ERROR:9478, expresso como:
$\omega_s c_z$
Por outro lado, os redemoinhos tendem a misturar a água, gerando uma difusão que transporta os sedimentos em direção à superfície. Esse fluxo, representado por la viscosidade turbulenta ($A$), é dado pelo gradiente de ERROR:9478 em la profundidade ($z$), igual a:
$A\displaystyle\frac{\partial c_z}{\partial z}$
A distribuição se forma quando os sedimentos alcançam o equilíbrio, onde o fluxo de sedimentação é igual à difusão gerada pelos redemoinhos em direção à superfície. Integrando ambos os termos da equação com o taxa de erosão ($E$) e o desigualdade ($d$), obtemos a distribuição:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
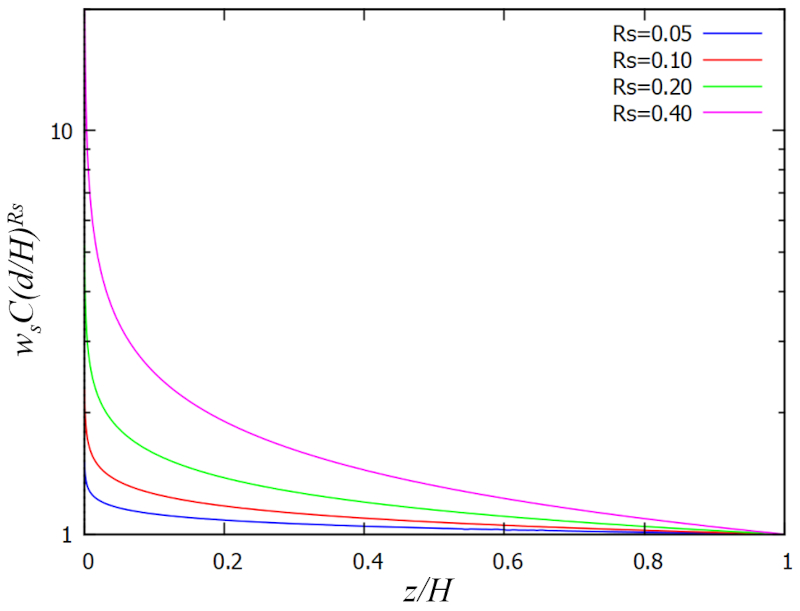
Após empregar a expressão obtida para la viscosidade turbulenta ($A$) com o fator de Rouse ($R_s$), la rugosidade ($k$) e la profundidade relativa ($\xi$), derivamos a expressão:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
que pode ser representada graficamente como:
ID:(15631, 0)
Processos de mistura em águas rasas
Modelo 
Os mecanismos de mistura em áreas rasas são gerados por diversos tipos de ondas. Entre eles estão as ondas internas, as ondas superficiais, a interação entre ondas e correntes, as marés e a quebra das ondas na costa.
Variáveis
Cálculos
Cálculos
Equações
Assim como la estresse cinemático ($\tau_x$) se relaciona com la viscosidade turbulenta ($A$) e la comprimento de mistura ($l$), tem-se que:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Se forem usados la constante de Karman ($\kappa$), la profundidade total ($H$) e la rugosidade ($k$):
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
e com la velocidade de fricção ($U_d$):
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
obt m-se:
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
(ID 12185)
Assim como la estresse cinemático ($\tau_x$) se relaciona com la viscosidade turbulenta ($A$), o perfil da velocidade ($u_z$) e la profundidade ($z$), ele definido por
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
e pode ser integrado de o desigualdade ($d$) a la profundidade ($z$) para obter a velocidade usando a seguinte express o:
$u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'$
Com a formula o de la viscosidade turbulenta ($A$) em termos de la profundidade relativa ($\xi$) juntamente com la profundidade total ($H$), la rugosidade ($k$) e la velocidade de fricção ($U_d$), e considerando que
a seguinte equa o para velocidade derivada:
$u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))$
onde
$\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)$
definido com
$\lambda=\sqrt{1-\xi}$
e
$\lambda=\sqrt{1-k}$
Visto que em grande parte da profundidade
$\ln(z/d) \gg \Phi(\xi,k)$
o perfil de velocidade pode ser simplificado para
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
(ID 12187)
Os sedimentos tendem a cair para o fundo com uma taxa de sedimentação ($\omega_s$), enquanto a difus o, que neste caso corresponde mistura gerada por turbilh es, induz um fluxo igual a la viscosidade turbulenta ($A$) e o gradiente de ERROR:9478 em la profundidade ($z$), da seguinte forma:
$A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0$
Integrando essa express o, obtemos:
$c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}$
com la comprimento de mistura ($l$):
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
temos:
$c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}$
o que resulta em:
$c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)$
com o fator de Rouse ($R_s$) e o número de despertar ($R_0$):
| $ R_s \equiv R_0 (1 - k )^{3/2}$ |
onde:
$\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}$
com:
$\lambda=\sqrt{1-\xi}$
e:
$\lambda=\sqrt{1-k}$
Como em grande parte da profundidade:
$\Phi\sim 1$
temos a distribui o de concentra o:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
(ID 12193)
Assim como la viscosidade turbulenta ($A$) se relaciona com la comprimento de mistura ($l$), o perfil da velocidade ($u_z$) e la profundidade ($z$) s o definidos como
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
e, dado que la estresse cinemático ($\tau_x$)
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
eliminar o gradiente resulta em
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
(ID 15633)
Exemplos
(ID 15614)
(ID 12196)
(ID 12200)
O número de Strouhal ($St$) est relacionado empiricamente com o número de Reynolds ($Re$). O número de Strouhal ($St$) est associado com la frequência de geração de vórtice ($\omega$), la velocidade de fricção ($U_d$) e la profundidade total ($H$)
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
Isso permite estimar, atrav s de o número de Reynolds ($Re$), a frequ ncia com que a concentra o pode trocar os componentes a serem difundidos. No entanto, deve-se ter em mente que o processo pode ser interrompido se a frequ ncia for menor do que a das mar s.

(ID 12199)
Se assumirmos que n o h vento na superf cie, pode-se supor que n o h tens o na superf cie. Portanto, haver apenas a tens o da gua no fundo. Esta tens o diminuir linearmente do fundo para a superf cie. Para simplificar a modelagem, pode-se usar a propor o entre la profundidade ($z$) e la profundidade total ($H$), o que nos d um fator adimensional la profundidade relativa ($\xi$). La estresse cinemático ($\tau_x$) ser , portanto, proporcional a
$\tau_x \propto 1-\xi$
Como la estresse cinemático ($\tau_x$) equivalente densidade de energia dividida pela densidade, o valor no fundo deve ser proporcional ao quadrado da velocidade no fundo. Isso descrito no modelo com la velocidade de fricção ($U_d$) e significa que
$\tau_x \propto U_d^2$
Finalmente, h o efeito de la rugosidade ($k$) do fundo do mar, ou seja, a propor o de o desigualdade ($d$) e la profundidade total ($H$). Isso significa que la estresse cinemático ($\tau_x$) deve ser corrigido por um fator an logo profundidade:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Assim, obt m-se um modelo da seguinte forma:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
que representado graficamente a seguir:

(ID 15630)
La comprimento de mistura ($l$) corresponde ao que poderia ser descrito como o tamanho dos v rtices. Pr ximo parede, esses v rtices s podem ter um tamanho m ximo igual dist ncia at a parede, que m nima. medida que nos aproximamos da superf cie, esses v rtices podem se tornar cada vez maiores, ent o a fun o deve atingir um m ximo nesse ponto.
Para simplificar a modelagem, pode-se usar a propor o entre la profundidade ($z$) e la profundidade total ($H$), o que nos proporciona um fator adimensional la profundidade relativa ($\xi$). Assim, uma fun o simples que atende a essa descri o :
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
Por outro lado, o modelo de camada limite de Prandtl mostra que estas s o uma fra o do fluxo com uma largura igual a la profundidade total ($H$) e uma propor o de la constante de Karman ($\kappa$), ent o:
$l \propto \kappa H$
Finalmente, devemos corrigir pelo efeito da rugosidade da mesma forma que para o estresse cinem tico:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Portanto, la comprimento de mistura ($l$) pode ser modelado da seguinte forma:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |

(ID 12201)
Quando Prandtl modela a forma o de turbilh es perto das paredes, ele estabelece a rela o entre la viscosidade turbulenta ($A$), la comprimento de mistura ($l$) e o gradiente de o perfil da velocidade ($u_z$) em la profundidade ($z$) da seguinte forma:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
Por outro lado, a for a viscosa t pica, que modelada como a viscosidade multiplicada pela superf cie de contato e o gradiente de velocidade, corresponde a la estresse cinemático ($\tau_x$) no caso das turbul ncias:
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
De ambas as equa es, surge a rela o:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Essa rela o permite calcular la viscosidade turbulenta ($A$) em fun o de la estresse cinemático ($\tau_x$) e la comprimento de mistura ($l$), que s o modelados neste caso. Assim, com la profundidade total ($H$), la velocidade de fricção ($U_d$), la rugosidade ($k$), la profundidade relativa ($\xi$) e la constante de Karman ($\kappa$):
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
que representado a seguir:

O resultado que a viscosidade turbulenta m xima na profundidade m dia e se reduz a valores m nimos tanto pr ximo ao fundo quanto pr ximo superf cie. Ou seja, nessas zonas a mistura e a perda de momento s o menores.
(ID 15624)
Como la estresse cinemático ($\tau_x$) igual a la viscosidade turbulenta ($A$) e ao gradiente de o perfil da velocidade ($u_z$) em rela o a la profundidade ($z$), poss vel integrar a equa o para obter o perfil de velocidade:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} dz'$
Ap s realizar a integra o e utilizando la velocidade de fricção ($U_d$), la constante de Karman ($\kappa$), la rugosidade ($k$) e la profundidade relativa ($\xi$), obt m-se:
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
Essa express o corresponde conhecida lei logar tmica do perfil de velocidades, desenvolvida por Prandtl e Schlichting.
O perfil resultante mostrado no gr fico a seguir:

Esse perfil tamb m permite relacionar ERROR:9467 com la velocidade de fricção ($U_d$) em fun o de la coeficiente de arrasto ($C_D$):
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
Al m disso, la coeficiente de arrasto ($C_D$) pode ser estimado a partir de la rugosidade ($k$) e la constante de Karman ($\kappa$) usando:
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
(ID 15623)
Se considerarmos o comportamento do material suspenso, observamos dois principais fatores. Primeiramente, h uma tend ncia de que ele se sedimente com uma velocidade la taxa de sedimentação ($\omega_s$), gerando um fluxo que depende de ERROR:9478, expresso como:
$\omega_s c_z$
Por outro lado, os redemoinhos tendem a misturar a gua, gerando uma difus o que transporta os sedimentos em dire o superf cie. Esse fluxo, representado por la viscosidade turbulenta ($A$), dado pelo gradiente de ERROR:9478 em la profundidade ($z$), igual a:
$A\displaystyle\frac{\partial c_z}{\partial z}$
A distribui o se forma quando os sedimentos alcan am o equil brio, onde o fluxo de sedimenta o igual difus o gerada pelos redemoinhos em dire o superf cie. Integrando ambos os termos da equa o com o taxa de erosão ($E$) e o desigualdade ($d$), obtemos a distribui o:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
Ap s empregar a express o obtida para la viscosidade turbulenta ($A$) com o fator de Rouse ($R_s$), la rugosidade ($k$) e la profundidade relativa ($\xi$), derivamos a express o:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
que pode ser representada graficamente como:

(ID 15631)
(ID 15618)
ID:(1629, 0)
