User:
Mixing processes in shallow waters
Storyboard 
Mixing mechanisms in shallow areas are generated by various types of waves. Among them are internal waves, surface waves, wave-current interaction, tides, and wave breaking on the coast.
ID:(1629, 0)
Mechanisms
Iframe
Mechanisms
ID:(15614, 0)
Shallow mixing mechanisms
Image
Para el caso en el borde costero en donde hay baja profundidad se tienen los siguientes mecanismos que contribuyen el mezclado de las aguas por efecto de:
• olas internas
adicionalmente existen contribuciones adicionales mediante
• mezcla por ola
• interacción de corriente con olas
• mezcla por mares
• mezcla por quiebre de olas en costa
De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
ID:(12196, 0)
Disturbance magnitudes
Image
Las perturbaciones se pueden ordenar en función de sus escalas de tiempo y dimensiones. El resultado se presenta en la siguiente grafica:
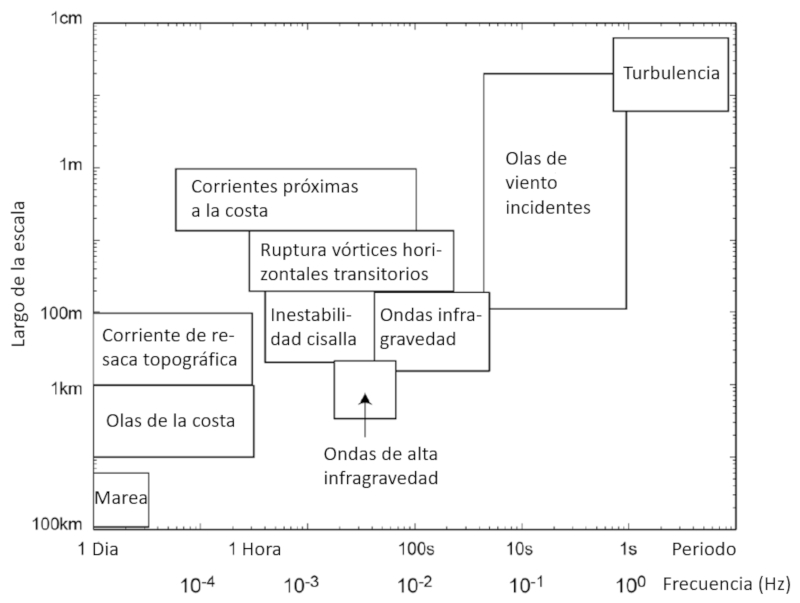
De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
ID:(12200, 0)
Strouhal number as a function of Reynold number
Image
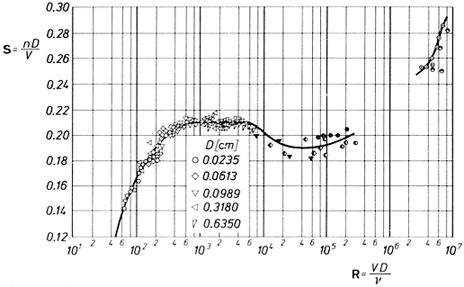
The strouhal number ($St$) is empirically related to the reynolds number ($Re$). The strouhal number ($St$) is associated with the vortex generation frequency ($\omega$), the friction speed ($U_d$), and the total depth ($H$) is
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
This allows estimating, via the reynolds number ($Re$), the frequency at which concentration can exchange the components to be diffused. However, it must be kept in mind that the process may be aborted if the frequency is lower than that of the tides.
ID:(12199, 0)
Kinematic stress
Description
If it is assumed that there is no wind on the surface, it can be assumed that there is no tension on it. Therefore, there will only be water tension at the bottom. This tension will decrease linearly from the bottom to the surface. To simplify the modeling, the proportion between the depth ($z$) and the total depth ($H$) can be used, giving us a dimensionless factor the relative depth ($\xi$). The kinematic stress ($\tau_x$) will, therefore, be proportional to
$\tau_x \propto 1-\xi$
Since the kinematic stress ($\tau_x$) is equivalent to the energy density divided by the density, the value at the bottom must be proportional to the square of the velocity at the bottom. This is described in the model with the friction speed ($U_d$) and means that
$\tau_x \propto U_d^2$
Finally, there is the effect of the rugosity ($k$) of the seabed, i.e., the proportion of the unevenness ($d$) and the total depth ($H$). This means that the kinematic stress ($\tau_x$) must be corrected by a factor analogous to depth:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Thus, a model of the form is obtained:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
which is graphed as follows:
ID:(15630, 0)
Mixing length
Description
The mixing length ($l$) corresponds to what could be described as the size of the vortices. Near the wall, these can only be as large as the distance to the wall, which is minimal. As we approach the surface, they can become increasingly larger, so the function should reach a maximum at this point.
To simplify the modeling, the proportion between the depth ($z$) and the total depth ($H$) can be used, giving us a dimensionless factor the relative depth ($\xi$). Thus, a simple function that meets this description is:
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
On the other hand, Prandtl's boundary layer model shows that these are a fraction of the flow with a width equal to the total depth ($H$) and a proportion of the karman constant ($\kappa$), so:
$l \propto \kappa H$
Finally, we must correct for the effect of roughness in the same way as for the kinematic stress:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Therefore, the mixing length ($l$) can be modeled as follows:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
ID:(12201, 0)
Eddy viscosity
Top
When Prandtl models the formation of eddies near walls, he establishes the relationship between the eddy viscosity ($A$), the mixing length ($l$), and the gradient of the velocity profile ($u_z$) in the depth ($z$) as follows:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
On the other hand, the typical viscous force, which is modeled as viscosity multiplied by the contact surface and the velocity gradient, corresponds to the kinematic stress ($\tau_x$) in the case of turbulence:
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
From both equations, the relationship emerges:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
This relationship allows calculating the eddy viscosity ($A$) as a function of the kinematic stress ($\tau_x$) and the mixing length ($l$), which are modeled in this case. Thus, with the total depth ($H$), the friction speed ($U_d$), the rugosity ($k$), the relative depth ($\xi$), and the karman constant ($\kappa$):
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
which is represented below:
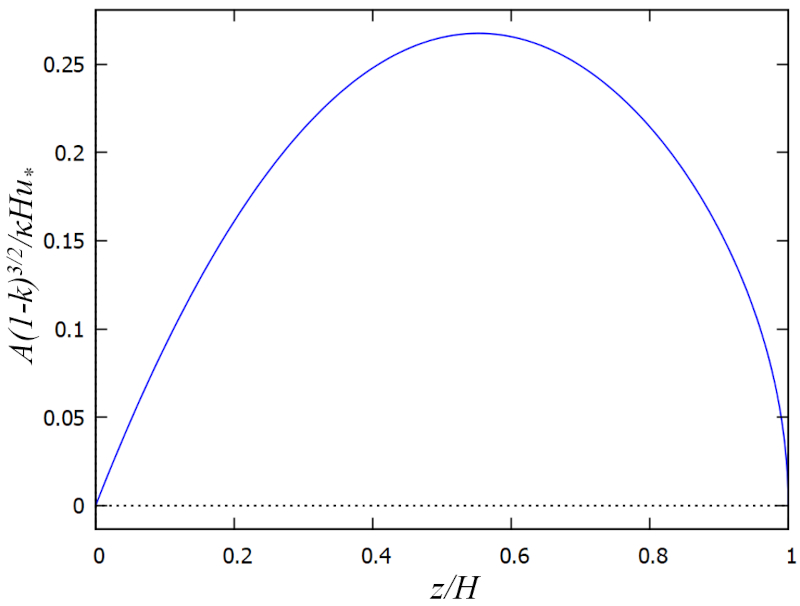
The result is that turbulent viscosity is maximal at mid-depth and reduces to minimal values both near the bottom and near the surface. In other words, in these zones, mixing and momentum loss are lower.
ID:(15624, 0)
Velocity profile
Top
Since the kinematic stress ($\tau_x$) is equal to the eddy viscosity ($A$) and the gradient of the velocity profile ($u_z$) in the depth ($z$), the equation can be integrated to obtain the velocity profile:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} , dz'$
After integrating this expression, with the friction speed ($U_d$), the karman constant ($\kappa$), the rugosity ($k$), and the relative depth ($\xi$), we obtain:
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
which corresponds to the famous logarithmic law developed by Prandtl and Schlichting.
The profile is shown in the following graph:
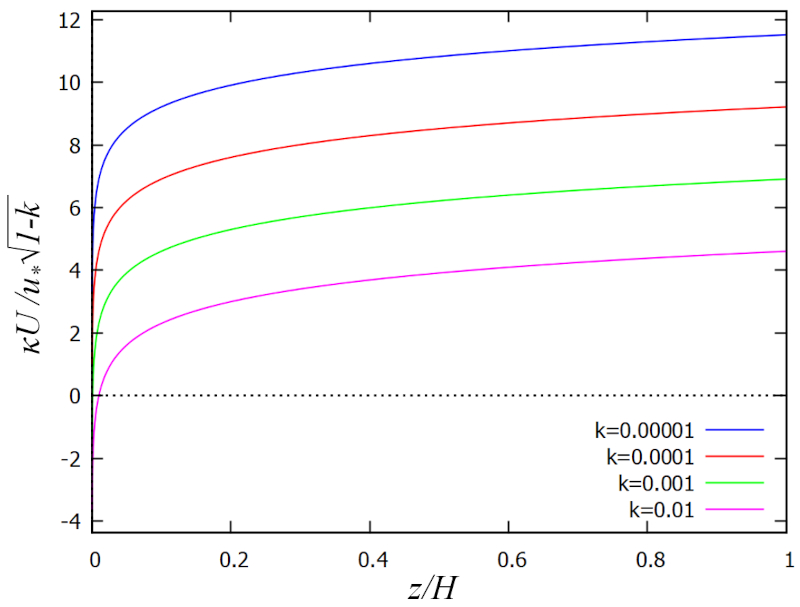
The profile also allows relating the velocidad en la superficie ($U$) with the friction speed ($U_d$) as a function of the rugosity ($k$) and the karman constant ($\kappa$), which in turn allows defining a the bottom drag ($C_D$) with:
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
and
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
ID:(15623, 0)
Sediment concentration
Top
If we consider the behavior of suspended material, we'll observe two main factors. Firstly, there's a tendency for it to sediment with a velocity the sedimentation rate ($\omega_s$), generating a flow dependent on the concentración de sedimentos ($c_z$), expressed as:
$\omega_s c_z$
On the other hand, eddies tend to mix the water, generating a diffusion that carries sediments towards the surface. This flow, represented by the eddy viscosity ($A$), is given by the gradient of the concentración de sedimentos ($c_z$) in the depth ($z$), equal to:
$A\displaystyle\frac{\partial c_z}{\partial z}$
The distribution forms when sediments reach equilibrium, where the sedimentation flow equals the diffusion generated by eddies towards the surface. Integrating both terms of the equation with the erosion rate ($E$) and the unevenness ($d$), we obtain the distribution:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
After employing the expression obtained for the eddy viscosity ($A$) with the rouse factor ($R_s$), the rugosity ($k$), and the relative depth ($\xi$), we derive the expression:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
which can be graphically represented as:
ID:(15631, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$
A = kappa * U_d * H * xi * (1- xi /2)*sqrt(1- xi )/(1- k )^(3/2)
$ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$
A = l ^2*@DIF( u_z , z )
$ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$
C_D = kappa ^2/((1- k )* log(1/ k )^2)
$ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$
c_z =( E / omega_s )*( k / xi )^ R_s
$ k \equiv \displaystyle\frac{ d }{ H }$
k = d / H
$ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$
l = kappa * H * xi *(1 - xi /2)/(1 - k )
$ R_0 \equiv \displaystyle\frac{ \omega_s }{ \kappa U_d }$
R_0 = omega_s /( kappa * U_d )
$ R_s \equiv R_0 (1 - k )^{3/2}$
R_s = R_0 (1 - k )^(3/2)
$ St \equiv \displaystyle\frac{ \omega H }{ U_d }$
St = omega * H / U_d
$ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$
tau_x = A *@DIF( u_z , z )
$ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$
tau_x = A ^2 / l ^2
$ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$
tau_x = U_d ^2 *(1- xi )/(1- k )
$ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$
U ^2 = U_d ^2/ C_D
$ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$
u_z = U_d sqrt(1- k )*log( xi / k ))/ kappa
$ \xi \equiv \displaystyle\frac{ z }{ H }$
xi = z / H
ID:(15618, 0)
Strouhal's number
Equation
The strouhal number ($St$) characterizes the vortex generation frequency ($\omega$). Compare the velocity associated with the vortex generation frequency ($\omega$) and its size with that of the flow represented by the total depth ($H$).
Therefore, with this, we have
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
ID:(12198, 0)
Bottom roughness
Equation
The behavior of the current and the turbulence to be generated or damped depends on the rugosity ($k$) of the seabed. This is defined by comparing the average profile of the unevenness ($d$) with the profile of the total depth ($H$) where it is located.
Therefore, it is defined that the rugosity ($k$) is
| $ k \equiv \displaystyle\frac{ d }{ H }$ |
ID:(12183, 0)
Relative depth
Equation
The relative depth ($\xi$) is defined in terms of the depth ($z$) and the total depth ($H$), expressed as follows:
| $ \xi \equiv \displaystyle\frac{ z }{ H }$ |
None
ID:(12182, 0)
Kinematic stress
Equation
For laminar flow, the viscose force ($F_v$) can be calculated from the parallel surfaces ($S$), the viscosity ($\eta$), the speed difference between surfaces ($\Delta v$), and the distance between surfaces ($\Delta z$) using the following equation:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
In the case of turbulent flow, an analogy can be established by defining a eddy viscosity ($A$) as the viscosity divided by density, associated with force per area and density, which we will call the kinematic stress ($\tau_x$), calculated in terms of the velocity profile ($u_z$) and the depth ($z$) as follows:
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
ID:(12191, 0)
Prandtl's Law
Equation
In 1925, Prandtl introduced the concept of a boundary layer where eddies mix the fluid and transfer momentum in a manner similar to how transfer at the molecular level is modeled, generating viscous behavior. The size of this zone is defined as the mixing length ($l$) and the effect is described with an analog to viscosity corresponding to the eddy viscosity ($A$). This can be estimated using the gradient of the velocity profile ($u_z$) in the depth ($z$) as follows:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
[1] Prandtl, Ludwig (1925). "Bericht über Untersuchungen zur ausgebildeten Turbulenz" (Report on Investigations in Developed Turbulence). Z. Angew. Math. Mech. 5 (2): 136.
ID:(12186, 0)
Kinematic stress relationship
Equation
The kinematic stress ($\tau_x$) can be calculated from the eddy viscosity ($A$) and the mixing length ($l$) using the following method:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Just as the eddy viscosity ($A$) is related to the mixing length ($l$), the velocity profile ($u_z$) and the depth ($z$) are defined as
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
and since the kinematic stress ($\tau_x$) is
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
eliminating the gradient yields
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
ID:(15633, 0)
Deeper ocean vortex diffusivity
Equation
The kinematic stress ($\tau_x$) will be maximal near the ocean floor and zero at the surface, provided there is no wind on the ocean's surface. Since it is associated with the friction speed ($U_d$) at the bottom but must be adjusted for the effect of the rugosity ($k$), it can be modeled based on the relative depth ($\xi$) as follows:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
ID:(12202, 0)
Mixing length
Equation
The mixing zone introduced by Prandtl, of size the mixing length ($l$), is estimated as a fraction of the order of the karman constant ($\kappa$) of the total depth ($H$). Additionally, it must be adjusted for the effect of the rugosity ($k$), and it should be noted that the mixing length ($l$) depends on the relative depth ($\xi$), being null at the bottom and approximately constant and maximal near the surface. Therefore, it can be modeled as follows:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
[1] Prandtl, Ludwig (1925). "Bericht über Untersuchungen zur ausgebildeten Turbulenz" (Report on Investigations in Developed Turbulence). Z. Angew. Math. Mech. 5 (2): 136.
ID:(12194, 0)
Eddy viscosity
Equation
A partir de mediciones, podemos modelar the eddy viscosity ($A$) con the relative depth ($\xi$), the total depth ($H$), the rugosity ($k$), the friction speed ($U_d$) y the karman constant ($\kappa$) mediante la expresión:
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
Just as the kinematic stress ($\tau_x$) relates to the eddy viscosity ($A$) and the mixing length ($l$), it follows that:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
If the karman constant ($\kappa$), the total depth ($H$), and the rugosity ($k$) are used:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
and with the friction speed ($U_d$):
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
we obtain:
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
ID:(12185, 0)
Velocity profile
Equation
The velocity profile ($u_z$) is a function of the relative depth ($\xi$) and the parameters the rugosity ($k$), the friction speed ($U_d$), and the karman constant ($\kappa$), represented as follows:
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
Just as the kinematic stress ($\tau_x$) relates to the eddy viscosity ($A$), the velocity profile ($u_z$), and the depth ($z$), it is defined by
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
and can be integrated from the unevenness ($d$) to the depth ($z$) to obtain the velocity using the following expression:
$u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'$
With the formulation of the eddy viscosity ($A$) in terms of the relative depth ($\xi$) along with the total depth ($H$), the rugosity ($k$), and the friction speed ($U_d$), and considering that
the following equation for velocity is derived:
$u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))$
where
$\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)$
is defined with
$\lambda=\sqrt{1-\xi}$
and
$\lambda=\sqrt{1-k}$
Since throughout much of the depth
$\ln(z/d) \gg \Phi(\xi,k)$
the velocity profile can be simplified to
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
ID:(12187, 0)
Damping coefficient
Equation
The velocidad en la superficie ($U$) is proportional to the friction speed ($U_d$), with a proportionality constant that depends on the karman constant ($\kappa$) and the rugosity ($k$), as follows:
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
ID:(12184, 0)
Surface speed
Equation
The friction speed ($U_d$) is proportional to the velocidad en la superficie ($U$), with the proportionality constant being the bottom drag ($C_D$), which represents the relationship between their respective kinetic energies:
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
ID:(12188, 0)
Diffusion of a sediment concentration
Equation
The concentración de sedimentos ($c_z$) is a function of the relative depth ($\xi$) that depends on the erosion rate ($E$), the sedimentation rate ($\omega_s$), the rugosity ($k$), and the rouse factor ($R_s$), and is calculated as follows:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
Sediments tend to settle to the bottom with a sedimentation rate ($\omega_s$), while diffusion, which in this case corresponds to the mixing generated by eddies, induces a flow equal to the eddy viscosity ($A$) and the gradient of the concentración de sedimentos ($c_z$) in the depth ($z$) as follows:
$A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0$
Integrating this expression gives:
$c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}$
with the mixing length ($l$):
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
we have:
$c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}$
which results in:
$c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)$
with the rouse factor ($R_s$) and the rouse number ($R_0$):
| $ R_s \equiv R_0 (1 - k )^{3/2}$ |
where:
$\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}$
with:
$\lambda=\sqrt{1-\xi}$
and:
$\lambda=\sqrt{1-k}$
Since throughout much of the depth:
$\Phi\sim 1$
we have the concentration distribution:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
ID:(12193, 0)
Rouse's number
Equation
The value the rouse number ($R_0$) compares the sedimentation speed, which competes with the diffusion associated with the current at the bottom. When combined with the sedimentation rate ($\omega_s$), the friction speed ($U_d$), and the karman constant ($\kappa$), it yields:
| $ R_0 \equiv \displaystyle\frac{ \omega_s }{ \kappa U_d }$ |
ID:(12195, 0)
The Rouse factor
Equation
The value the rouse number ($R_0$) assesses the sedimentation speed, which competes with the diffusion linked to the current at the bottom. Combined with the sedimentation rate ($\omega_s$), the friction speed ($U_d$), and the karman constant ($\kappa$), it yields:
| $ R_0 \equiv \displaystyle\frac{ \omega_s }{ \kappa U_d }$ |
In cases where the seafloor is not smooth, the rugosity ($k$) exists and leads to a correction of the Rouse number, which we call the Rouse factor:
| $ R_s \equiv R_0 (1 - k )^{3/2}$ |
ID:(15632, 0)