Processo de mistura em águas profundas
Storyboard 
Em maiores profundidades, os mecanismos de dissipação de energia dos vórtices estão relacionados com a viscosidade e a flutuabilidade. Qual deles domina depende da situação e pode ser determinado utilizando números característicos associados a ambos os fenômenos.[1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
ID:(1628, 0)
Energia cinética dissipada pelo vórtice
Conceito 
Em geral, a dissipação de energia ocorre em função do tempo considerado, então deve-se comparar la energia cinética ($\epsilon_v$) com uma tempo característico ($\tau$) de modo que
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
Existem dois tipos de processos que reduzem a energia dos vórtices até que se tornem flutuações térmicas. Por um lado, há a difusão de momento ou viscosidade, enquanto por outro lado há a flotação.
A perda de la energia cinética ($\epsilon_v$) varia em função de la energia dissipada pela viscosidade ($\epsilon_{\eta}$) e la energia dissipada por flutuação ($\epsilon_{\rho}$) em la tempo característico ($\tau$) como:
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau } $ |
ID:(15621, 0)
Variação da energia cinética
Conceito 
Como la energia cinética ($\epsilon_v$), onde para simplificação, negligenciamos o fator de 1/2 e ela depende de la densidade média ($\rho$) e la velocidade do vórtice ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
a perda de energia será essa energia por la tempo característico ($\tau$), que com la comprimento de mistura ($l$) é
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a variação é
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
ID:(15608, 0)
Perda de energia devido à viscosidade
Conceito 
Como la energia dissipada pela viscosidade ($\epsilon_{\eta}$) está relacionado con la viscosidade da água do oceano ($\eta$), la velocidade do vórtice ($v_l$) y la comprimento de mistura ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
a perda de energia será essa energia por la tempo característico ($\tau$), que com la comprimento de mistura ($l$) é
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a variação é
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
ID:(15609, 0)
Perda de energia devido à flutuação
Conceito 
Como la energia dissipada por flutuação ($\epsilon_{\rho}$) está relacionado com ERROR:9484, la aceleração gravitacional ($g$) e la comprimento de mistura ($l$):
$\epsilon_{\rho} =\Delta\rho g l$
a perda de energia será essa energia por la tempo característico ($\tau$), que é
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a variação é
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
ID:(15610, 0)
Amortecimento de viscosidade
Conceito 
No caso em que os processos difusivos são mais relevantes do que os de flutuação, observa-se que com la energia cinética ($\epsilon_v$), la energia dissipada por flutuação ($\epsilon_{\rho}$) e la energia dissipada pela viscosidade ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Dado que com la tempo característico ($\tau$), la energia cinética ($\epsilon_v$) é
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada pela viscosidade ($\epsilon_{\eta}$) é
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
a existência do vórtice implica que sua energia cinética é maior do que a perda, então com
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
resulta na exigência de que se deve ser o caso de
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
ID:(15612, 0)
Amortecimento de flutuação
Conceito 
No caso em que com la energia cinética ($\epsilon_v$), la energia dissipada pela viscosidade ($\epsilon_{\eta}$) e la energia dissipada por flutuação ($\epsilon_{\rho}$) são tais que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Dado que la energia cinética ($\epsilon_v$) é com la densidade ($\rho$), la comprimento de mistura ($l$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada por flutuação ($\epsilon_{\rho}$) é com ERROR:9484, la aceleração gravitacional ($g$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
a existência do vórtice implica que sua energia cinética é maior do que a perda, então com
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
resulta na exigência de que com o número Richardson ($R_i$) deve satisfazer
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
ID:(15611, 0)
Relação dos números de Richardson e Reynolds
Descrição 
A relação entre ERROR:8614 com la densidade ($\rho$), la velocidade do vórtice ($v_l$), la viscosidade da água do oceano ($\eta$) e ERROR:9112 é dada por
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
e o número Richardson ($R_i$) com ERROR:9484 e la aceleração gravitacional ($g$) é representada por
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
como mostrado no gráfico abaixo, onde ambos os casos limites marcam as situações de limite de estabilidade:
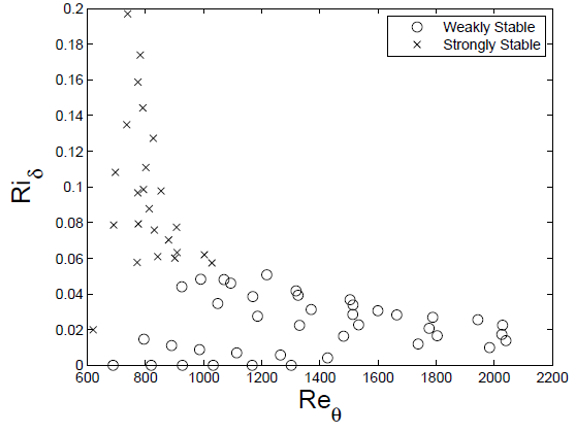
ID:(12211, 0)
Processo de mistura em águas profundas
Modelo 
Em maiores profundidades, os mecanismos de dissipação de energia dos vórtices estão relacionados com a viscosidade e a flutuabilidade. Qual deles domina depende da situação e pode ser determinado utilizando números característicos associados a ambos os fenômenos. [1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
Variáveis
Cálculos
Cálculos
Equações
A perda dos v rtices envolve la energia dissipada pela viscosidade ($\epsilon_{\eta}$) com la viscosidade da água do oceano ($\eta$), la velocidade do vórtice ($v_l$) e la comprimento de mistura ($l$).
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
A perda de energia devido a la tempo característico ($\tau$), que
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
descrita por
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
(ID 12207)
Como la energia dissipada por flutuação ($\epsilon_{\rho}$) igual a ERROR:9484, la aceleração gravitacional ($g$) e dist ncia percorrida ($\Delta z$),
$\epsilon_{\rho} =\Delta\rho g \Delta z$
a perda de energia ser esta energia por la tempo característico ($\tau$), que com la comprimento de mistura ($l$)
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
portanto, com la velocidade do vórtice ($v_l$),
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
(ID 12208)
No caso em que os processos difusivos s o mais relevantes do que a flutua o, temos que com la energia cinética ($\epsilon_v$), la energia dissipada por flutuação ($\epsilon_{\rho}$) e la energia dissipada pela viscosidade ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
J que com la tempo característico ($\tau$), la energia cinética ($\epsilon_v$) e la densidade média ($\rho$)
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada pela viscosidade ($\epsilon_{\eta}$)
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
a exist ncia do v rtice implica que sua energia cin tica maior do que a perda, ent o com
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
o requisito de que o número de Reynolds ($Re$) deve ser
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
(ID 12209)
No caso de com la energia cinética ($\epsilon_v$), la energia dissipada pela viscosidade ($\epsilon_{\eta}$) e la energia dissipada por flutuação ($\epsilon_{\rho}$) serem tais que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Dado que la energia cinética ($\epsilon_v$) est com la densidade média ($\rho$), la comprimento de mistura ($l$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada por flutuação ($\epsilon_{\rho}$) est com ERROR:9484, la aceleração gravitacional ($g$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
a exist ncia do v rtice implica que sua energia cin tica maior do que a perda, ent o com
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
surge a exig ncia de que o número Richardson ($R_i$) deve satisfazer
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
(ID 12210)
Como la energia cinética ($\epsilon_v$) dos v rtices depende de la densidade média ($\rho$) e la velocidade do vórtice ($v_l$) de acordo com
$\epsilon_v =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
Como la tempo característico ($\tau$) com la comprimento de mistura ($l$)
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
temos que
$\displaystyle\frac{\epsilon_v}{\tau} =\rho \displaystyle\frac{v_l^3}{l}$
ou seja
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
(ID 12212)
Exemplos
(ID 15616)
Em geral, a dissipa o de energia ocorre em fun o do tempo considerado, ent o deve-se comparar la energia cinética ($\epsilon_v$) com uma tempo característico ($\tau$) de modo que
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
Existem dois tipos de processos que reduzem a energia dos v rtices at que se tornem flutua es t rmicas. Por um lado, h a difus o de momento ou viscosidade, enquanto por outro lado h a flota o.
A perda de la energia cinética ($\epsilon_v$) varia em fun o de la energia dissipada pela viscosidade ($\epsilon_{\eta}$) e la energia dissipada por flutuação ($\epsilon_{\rho}$) em la tempo característico ($\tau$) como:
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau } $ |
(ID 15621)
Como la energia cinética ($\epsilon_v$), onde para simplifica o, negligenciamos o fator de 1/2 e ela depende de la densidade média ($\rho$) e la velocidade do vórtice ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
a perda de energia ser essa energia por la tempo característico ($\tau$), que com la comprimento de mistura ($l$)
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a varia o
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
(ID 15608)
Como la energia dissipada pela viscosidade ($\epsilon_{\eta}$) est relacionado con la viscosidade da água do oceano ($\eta$), la velocidade do vórtice ($v_l$) y la comprimento de mistura ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
a perda de energia ser essa energia por la tempo característico ($\tau$), que com la comprimento de mistura ($l$)
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a varia o
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
(ID 15609)
Como la energia dissipada por flutuação ($\epsilon_{\rho}$) est relacionado com ERROR:9484, la aceleração gravitacional ($g$) e la comprimento de mistura ($l$):
$\epsilon_{\rho} =\Delta\rho g l$
a perda de energia ser essa energia por la tempo característico ($\tau$), que
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
e assim, a varia o
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
(ID 15610)
No caso em que os processos difusivos s o mais relevantes do que os de flutua o, observa-se que com la energia cinética ($\epsilon_v$), la energia dissipada por flutuação ($\epsilon_{\rho}$) e la energia dissipada pela viscosidade ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Dado que com la tempo característico ($\tau$), la energia cinética ($\epsilon_v$)
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada pela viscosidade ($\epsilon_{\eta}$)
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
a exist ncia do v rtice implica que sua energia cin tica maior do que a perda, ent o com
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
resulta na exig ncia de que se deve ser o caso de
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
(ID 15612)
No caso em que com la energia cinética ($\epsilon_v$), la energia dissipada pela viscosidade ($\epsilon_{\eta}$) e la energia dissipada por flutuação ($\epsilon_{\rho}$) s o tais que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Dado que la energia cinética ($\epsilon_v$) com la densidade ($\rho$), la comprimento de mistura ($l$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
e la energia dissipada por flutuação ($\epsilon_{\rho}$) com ERROR:9484, la aceleração gravitacional ($g$) e la velocidade do vórtice ($v_l$) em la tempo característico ($\tau$),
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
a exist ncia do v rtice implica que sua energia cin tica maior do que a perda, ent o com
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
resulta na exig ncia de que com o número Richardson ($R_i$) deve satisfazer
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
(ID 15611)
A rela o entre ERROR:8614 com la densidade ($\rho$), la velocidade do vórtice ($v_l$), la viscosidade da água do oceano ($\eta$) e ERROR:9112 dada por
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
e o número Richardson ($R_i$) com ERROR:9484 e la aceleração gravitacional ($g$) representada por
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
como mostrado no gr fico abaixo, onde ambos os casos limites marcam as situa es de limite de estabilidade:

(ID 12211)
(ID 15620)
ID:(1628, 0)
