Processus de mélange en eau profonde
Storyboard 
Dans le cas de profondeurs plus importantes, les mécanismes de dissipation d'énergie des tourbillons sont liés à la viscosité et à la flottabilité. Lequel domine dépend de la situation et peut être déterminé à l'aide des nombres caractéristiques associés à ces deux phénomènes.[1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
ID:(1628, 0)
Énergie cinétique dissipée par le vortex
Concept 
En général, la dissipation d'énergie se produit en fonction du temps considéré, donc a énergie cinétique ($\epsilon_v$) devrait être comparé à Une temps caractéristique ($\tau$) de manière à ce que
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
Il existe deux types de processus qui réduisent l'énergie des vortex jusqu'à ce qu'ils deviennent des fluctuations thermiques. D'un côté, il y a la diffusion de moment ou la viscosité, tandis que de l'autre côté, il y a la flottation.
La perte de a énergie cinétique ($\epsilon_v$) varie en fonction de a énergie dissipée par la viscosité ($\epsilon_{\eta}$) et a énergie dissipée par flottation ($\epsilon_{\rho}$) en a temps caractéristique ($\tau$) comme :
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau } $ |
ID:(15621, 0)
Variation de l'énergie cinétique
Concept 
Comme a énergie cinétique ($\epsilon_v$), où pour simplification, nous négligeons le facteur de 1/2 et elle dépend de a densité moyenne ($\rho$) et a vitesse du vortex ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
la perte d'énergie sera cette énergie par a temps caractéristique ($\tau$), qui avec a longueur de mélange ($l$) est
et donc, la variation est
ID:(15608, 0)
Perte d'énergie due à la viscosité
Concept 
Comme a énergie dissipée par la viscosité ($\epsilon_{\eta}$) est avec a viscosité de l'eau des océans ($\eta$), a vitesse du vortex ($v_l$) et a longueur de mélange ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
la perte d'énergie sera cette énergie par a temps caractéristique ($\tau$), qui avec a longueur de mélange ($l$) est
et ainsi, la variation est
ID:(15609, 0)
Perte d'énergie due à la flottaison
Concept 
Comme a énergie dissipée par flottation ($\epsilon_{\rho}$) est lié à ERROR:9484, a accélération gravitationnelle ($g$) et à A longueur de mélange ($l$) :
$\epsilon_{\rho} =\Delta\rho g l$
la perte d'énergie sera cette énergie par a temps caractéristique ($\tau$), qui est
et donc, la variation est
ID:(15610, 0)
Amortissement de la viscosité
Concept 
Dans le cas où les processus de diffusion sont plus pertinents que ceux de flottaison, on constate que avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par flottation ($\epsilon_{\rho}$) et a énergie dissipée par la viscosité ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Étant donné que avec a temps caractéristique ($\tau$), a énergie cinétique ($\epsilon_v$) est
et a énergie dissipée par la viscosité ($\epsilon_{\eta}$) est
l'existence du tourbillon implique que son énergie cinétique est supérieure à la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
il en résulte l'exigence selon laquelle il doit être le cas que
ID:(15612, 0)
Amortissement de la flottaison
Concept 
Dans le cas où avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par la viscosité ($\epsilon_{\eta}$) et a énergie dissipée par flottation ($\epsilon_{\rho}$) sont tels que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Étant donné que a énergie cinétique ($\epsilon_v$) est avec a densité ($\rho$), a longueur de mélange ($l$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
et a énergie dissipée par flottation ($\epsilon_{\rho}$) est avec ERROR:9484, a accélération gravitationnelle ($g$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
l'existence du tourbillon implique que son énergie cinétique est supérieure à la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
résulte en l'exigence selon laquelle avec le numéro de Richardson ($R_i$) doit satisfaire
ID:(15611, 0)
Relation numérique de Richardson et Reynolds
Description 
La relation entre ERROR:8614 avec a densité ($\rho$), a vitesse du vortex ($v_l$), a viscosité de l'eau des océans ($\eta$) et ERROR:9112 est donnée par
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
et le numéro de Richardson ($R_i$) avec ERROR:9484 et a accélération gravitationnelle ($g$) est représentée par
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
comme illustré dans le graphique ci-dessous, où les deux cas limites marquent les situations de limite de stabilité :
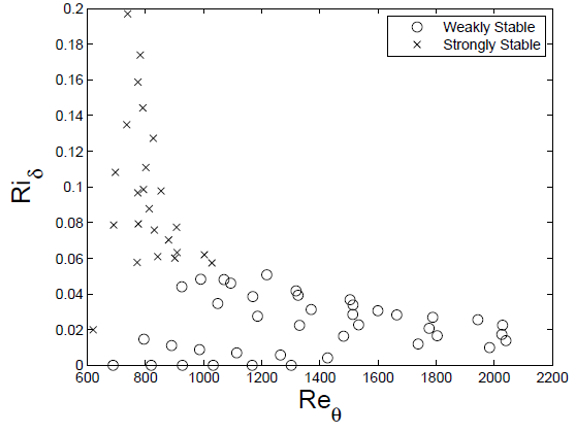
ID:(12211, 0)
Processus de mélange en eau profonde
Modèle 
Dans le cas de profondeurs plus importantes, les mécanismes de dissipation d'énergie des tourbillons sont liés à la viscosité et à la flottabilité. Lequel domine dépend de la situation et peut être déterminé à l'aide des nombres caractéristiques associés à ces deux phénomènes. [1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
Variables
Calculs
Calculs
Équations
La perte des tourbillons implique a énergie dissipée par la viscosité ($\epsilon_{\eta}$) avec a viscosité de l'eau des océans ($\eta$), a vitesse du vortex ($v_l$) et a longueur de mélange ($l$).
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
La perte d' nergie due a temps caractéristique ($\tau$), qui est
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
est d crite par
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
(ID 12207)
Puisque a énergie dissipée par flottation ($\epsilon_{\rho}$) est gal ERROR:9484, a accélération gravitationnelle ($g$) et la distance parcourue ($\Delta z$),
$\epsilon_{\rho} =\Delta\rho g \Delta z$
la perte d' nergie sera cette nergie par a temps caractéristique ($\tau$), qui avec a longueur de mélange ($l$) est
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
donc avec a vitesse du vortex ($v_l$), c'est
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
(ID 12208)
Dans le cas o les processus de diffusion sont plus pertinents que ceux de flottaison, nous avons que avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par flottation ($\epsilon_{\rho}$) et a énergie dissipée par la viscosité ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
tant donn que avec a temps caractéristique ($\tau$), a énergie cinétique ($\epsilon_v$) est
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
et a énergie dissipée par la viscosité ($\epsilon_{\eta}$) est
| $ \displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$ |
l'existence du tourbillon implique que son nergie cin tique est sup rieure la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
Puisqu'avec a temps caractéristique ($\tau$), a énergie cinétique ($\epsilon_v$) et a densité moyenne ($\rho$) c'est
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
(ID 12209)
Dans le cas o avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par la viscosité ($\epsilon_{\eta}$) et a énergie dissipée par flottation ($\epsilon_{\rho}$) sont tels que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
tant donn que a énergie cinétique ($\epsilon_v$) est avec a densité moyenne ($\rho$), a longueur de mélange ($l$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
et a énergie dissipée par flottation ($\epsilon_{\rho}$) est avec ERROR:9484, a accélération gravitationnelle ($g$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
| $ \displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l $ |
l'existence du tourbillon implique que son nergie cin tique est sup rieure la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
la condition est que le numéro de Richardson ($R_i$) doit satisfaire
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
(ID 12210)
Comme a énergie cinétique ($\epsilon_v$) des tourbillons d pend de a densité moyenne ($\rho$) et a vitesse du vortex ($v_l$) selon
$\epsilon_v =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
Comme a temps caractéristique ($\tau$) avec a longueur de mélange ($l$) est
| $ \tau = \displaystyle\frac{ l }{ v_l }$ |
on a que
$\displaystyle\frac{\epsilon_v}{\tau} =\rho \displaystyle\frac{v_l^3}{l}$
ce qui signifie
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$ |
(ID 12212)
Exemples
(ID 15616)
En g n ral, la dissipation d' nergie se produit en fonction du temps consid r , donc a énergie cinétique ($\epsilon_v$) devrait tre compar une temps caractéristique ($\tau$) de mani re ce que
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
Il existe deux types de processus qui r duisent l' nergie des vortex jusqu' ce qu'ils deviennent des fluctuations thermiques. D'un c t , il y a la diffusion de moment ou la viscosit , tandis que de l'autre c t , il y a la flottation.
La perte de a énergie cinétique ($\epsilon_v$) varie en fonction de a énergie dissipée par la viscosité ($\epsilon_{\eta}$) et a énergie dissipée par flottation ($\epsilon_{\rho}$) en a temps caractéristique ($\tau$) comme :
| $ \displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau } $ |
(ID 15621)
Comme a énergie cinétique ($\epsilon_v$), o pour simplification, nous n gligeons le facteur de 1/2 et elle d pend de a densité moyenne ($\rho$) et a vitesse du vortex ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
la perte d' nergie sera cette nergie par a temps caractéristique ($\tau$), qui avec a longueur de mélange ($l$) est
et donc, la variation est
(ID 15608)
Comme a énergie dissipée par la viscosité ($\epsilon_{\eta}$) est avec a viscosité de l'eau des océans ($\eta$), a vitesse du vortex ($v_l$) et a longueur de mélange ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
la perte d' nergie sera cette nergie par a temps caractéristique ($\tau$), qui avec a longueur de mélange ($l$) est
et ainsi, la variation est
(ID 15609)
Comme a énergie dissipée par flottation ($\epsilon_{\rho}$) est li ERROR:9484, a accélération gravitationnelle ($g$) et a longueur de mélange ($l$) :
$\epsilon_{\rho} =\Delta\rho g l$
la perte d' nergie sera cette nergie par a temps caractéristique ($\tau$), qui est
et donc, la variation est
(ID 15610)
Dans le cas o les processus de diffusion sont plus pertinents que ceux de flottaison, on constate que avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par flottation ($\epsilon_{\rho}$) et a énergie dissipée par la viscosité ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
tant donn que avec a temps caractéristique ($\tau$), a énergie cinétique ($\epsilon_v$) est
et a énergie dissipée par la viscosité ($\epsilon_{\eta}$) est
l'existence du tourbillon implique que son nergie cin tique est sup rieure la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
il en r sulte l'exigence selon laquelle il doit tre le cas que
(ID 15612)
Dans le cas o avec a énergie cinétique ($\epsilon_v$), a énergie dissipée par la viscosité ($\epsilon_{\eta}$) et a énergie dissipée par flottation ($\epsilon_{\rho}$) sont tels que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
tant donn que a énergie cinétique ($\epsilon_v$) est avec a densité ($\rho$), a longueur de mélange ($l$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
et a énergie dissipée par flottation ($\epsilon_{\rho}$) est avec ERROR:9484, a accélération gravitationnelle ($g$) et a vitesse du vortex ($v_l$) dans a temps caractéristique ($\tau$),
l'existence du tourbillon implique que son nergie cin tique est sup rieure la perte, donc avec
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
r sulte en l'exigence selon laquelle avec le numéro de Richardson ($R_i$) doit satisfaire
(ID 15611)
La relation entre ERROR:8614 avec a densité ($\rho$), a vitesse du vortex ($v_l$), a viscosité de l'eau des océans ($\eta$) et ERROR:9112 est donn e par
| $ Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$ |
et le numéro de Richardson ($R_i$) avec ERROR:9484 et a accélération gravitationnelle ($g$) est repr sent e par
| $ R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$ |
comme illustr dans le graphique ci-dessous, o les deux cas limites marquent les situations de limite de stabilit :

(ID 12211)
(ID 15620)
ID:(1628, 0)
