Difusión
Bild 
La difusión se origina por la diferencia de concentración de las partículas. Si otras palabras, al existir un numero mayor de partículas en una zona respecto de una segunda existe una mayor probabilidad que pase de esta a la segunda que a la inversa.

ID:(12139, 0)
Calculo de concentraciones
Bild 
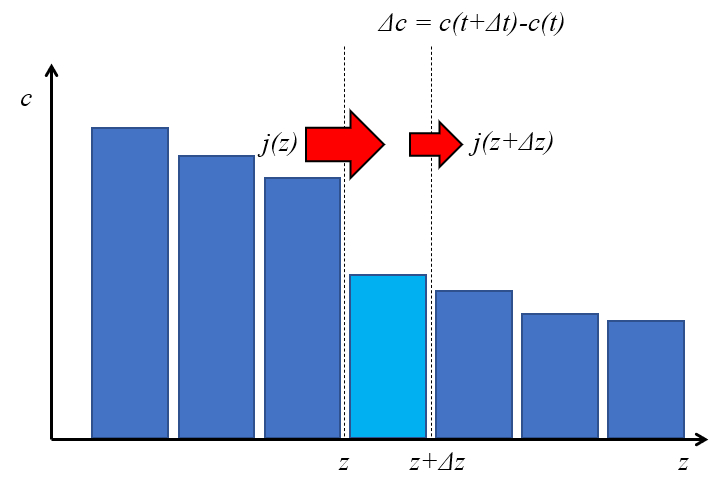
Para determinar la concentración en un punto se necesita calcular las cantidades que ingresan y las que salen de un volumen. Por ello para un espacio entre dos posición se considera el flujo que entra en restar lo que sale. Por ello la variación de la cantidad es igual a la concentración por el largo del segmento que es a su vez igual a el flujo por el tiempo considerado:
ID:(12141, 0)
Forma de la distribución
Bild 
La distribución obtenida corresponde con diffusionskonstante $m^2/s$, konzentration $1/m^3$, position $m$ und zeit $s$ a :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
que corresponde a una distribución de Gauss y que se muestra a continuación.
ID:(12142, 0)
Diffusionsprozesse
Modell 
Diffusion tritt auf, wenn es einen Konzentrationsunterschied zwischen verschiedenen Bereichen gibt, wodurch sich Teilchen von Bereichen höherer Konzentration zu Bereichen niedrigerer Konzentration bewegen. Der resultierende Fluss hängt von der Größe dieses Unterschieds und der Entfernung ab, über die er auftritt. Durch die Analyse, wie sich dieser Fluss zwischen zwei Punkten im Laufe der Zeit verändert, gelangt man zu einem Ausdruck, der die lokale Veränderung der Konzentration beschreibt. Wenn die Diffusionsgeschwindigkeit konstant ist, vereinfacht sich dieser Ausdruck und beschreibt eine glockenförmige Verteilung, die sich mit der Zeit und dem Ort verändert. Diese Verteilung wird mit der Zeit breiter, während ihre maximale Höhe proportional abnimmt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Flussdichte ($j$) h ngt von die Diffusionskonstante ($D$) und vom Gradienten ab, der aus die Variación de la concentración ($\Delta c$) und die Distanz ($\Delta z$) abgesch tzt wird:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Im Grenzfall, in dem die diskreten Intervalle in infinitesimale Differentiale bergehen ($\Delta z \rightarrow dz$), ergibt sich f r die Konzentration ($c$) und die Position ($z$):
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 12140)
Die Variación de la concentración ($\Delta c$) variiert mit die Zeitdauer ($\Delta t$) in Abh ngigkeit von die Variation der Flussdichte ($\Delta j$), die ihrerseits von die Distanz ($\Delta z$) abh ngt:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
Im Grenzfall, in dem diskrete Intervalle in infinitesimale Differentiale bergehen ($\Delta z \rightarrow dz$, $\Delta t \rightarrow dt$), ergibt sich f r die Konzentration ($c$), die Flussdichte ($j$), die Position ($z$) und der Zeit ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 12144)
Das zweite Ficksche Gesetz besagt, dass die nderung von die Konzentration ($c$) in Bezug auf der Zeit ($t$) gleich der nderung von die Flussdichte ($j$) in Bezug auf die Position ($z$) ist:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
Mit der Beziehung f r die Flussdichte ($j$):
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
ergibt sich daraus die Diffusionsgleichung:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
(ID 12145)
Das zweite Ficksche Gesetz, das die Konzentration ($c$), die Diffusionskonstante ($D$), die Position ($z$) und der Zeit ($t$) miteinander verkn pft, wird wie folgt ausgedr ckt:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
F r den Fall, dass die Diffusionskonstante ($D$) konstant ist, vereinfacht sich diese Gleichung zu:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 12146)
Die Differentialgleichung, die die Konzentration ($c$) beschreibt, unter der Annahme, dass die Diffusionskonstante ($D$) konstant ist, wird in Abh ngigkeit von die Position ($z$) und der Zeit ($t$) formuliert:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
deren L sung lautet:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 12147)
Im Fall einer Diffusion mit konstantem die Diffusionskonstante ($D$) ergibt sich f r die Verteilung von die Konzentration ($c$) in Abh ngigkeit von die Position ($z$) und der Zeit ($t$) folgende Form:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Wird die Standardabweichung ($\sigma$) in folgender Form eingef hrt:
| $ \sigma =\sqrt{2 D t }$ |
so l sst sich die Verteilung umschreiben zu:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16189)
Die Konzentration ($c$) wird von die Geschwindigkeit des Mediums ($u$) beeinflusst, das dem durch die Diffusionskonstante ($D$) beschriebenen Diffusionsprozess im positiven Bereich von die Position ($z$) entgegenwirkt und so die Verteilung in der Zeit ($t$) ver ndert gem :
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
Die L sung dieser Gleichung hat die folgende Form:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
(ID 16193)
Beispiele
Diffusion entsteht durch Unterschiede in der Teilchenkonzentration. Anders ausgedr ckt: Wenn sich in einer Region mehr Teilchen befinden als in einer anderen, ist die Wahrscheinlichkeit gr er, dass sie sich von der Region mit h herer Konzentration zur Region mit niedrigerer Konzentration bewegen und nicht umgekehrt.

(ID 12139)
In Fl ssigkeiten oder Gasen k nnen Situationen auftreten, in denen die Konzentration einer bestimmten Eigenschaft (z.B. einer Substanz, W rme oder Impuls) nicht homogen ist.
In solchen F llen ist es wahrscheinlicher, dass sich Teilchen mit dieser Eigenschaft von Bereichen h herer Konzentration in solche niedriger Konzentration bewegen einfach, weil es in der ersten Region mehr Teilchen gibt. Der Fluss h ngt daher sowohl von der Konzentrationsdifferenz als auch von der zur ckzulegenden Strecke ab also vom Konzentrationsgradienten.
Wenn die Konzentration an einem Punkt $z$ der L sung $c(z)$ betr gt und an einem anderen Punkt $z + \Delta z$ den Wert $c(z + \Delta z)$ hat, ergibt sich laut die Variación de la concentración ($\Delta c$):
$\Delta c = c(z + \Delta z) - c(z)$
Der Gradient ergibt sich dann gem die Distanz ($\Delta z$):
$\displaystyle\frac{c(z + \Delta z) - c(z)}{\Delta z} = \displaystyle\frac{\Delta c}{\Delta z} \sim \displaystyle\frac{\partial c}{\partial z}$
Gem die Flussdichte ($j$) ist der Fluss proportional zu diesem Gradienten, und die Proportionalit tskonstante wird als die Diffusionskonstante ($D$) bezeichnet.
Daraus ergibt sich:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Diese Gleichung ist als erstes Ficksches Gesetz bekannt.
(ID 16180)
Um einen Ausdruck f r den Fluss an einem bestimmten Punkt und nicht einen Mittelwert zu erhalten, wird der infinitesimale Grenzwert der Flussdifferentiale betrachtet. In diesem Fall wird die Flussdichte ($j$) in Abh ngigkeit von die Diffusionskonstante ($D$), die Variación de la concentración ($\Delta c$) und die Distanz ($\Delta z$) wie folgt dargestellt:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Dieser Grenzwert f hrt zum sogenannten ersten Fickschen Gesetz, das in seiner kontinuierlichen Form mit die Konzentration ($c$) und die Position ($z$) wie folgt geschrieben wird:
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 16181)
Um die Konzentration an einem Punkt zu bestimmen, m ssen die ein- und ausstr menden Mengen in einem Kontrollvolumen berechnet werden. Daher wird in einem Bereich zwischen zwei Positionen der einstr mende minus der ausstr mende Fluss betrachtet. Die Ver nderung der enthaltenen Menge entspricht dann der Konzentration multipliziert mit der L nge des Segments, was wiederum dem Nettostrom mal dem betrachteten Zeitintervall entspricht.

(ID 12141)
Wenn ein Element von die Distanz ($\Delta z$) ber ein Zeitintervall die Zeitdauer ($\Delta t$) betrachtet wird, gilt gem die Flussdichte ($j$):
• An der Position $z$ tritt ein Fluss von $j(z), \Delta t$ ein
• An der Position $z + \Delta z$ verl sst ein Fluss von $j(z + \Delta z), \Delta t$ das Element
Gem die Variation der Flussdichte ($\Delta j$) ergibt sich eine nderung des Inhalts von $\Delta c, \Delta z$.
Daher ergibt sich die Massenbilanz wie folgt:
$ \Delta c, \Delta z = \left[-j(z) + j(z + \Delta z)\right] \Delta t = -\Delta j, \Delta t $
Dies f hrt zur folgenden grundlegenden Beziehung:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
(ID 16182)
Um die Konzentration an einem bestimmten Punkt zu berechnen, muss von der gemittelten zur lokalen Darstellung bergegangen werden. Unter Verwendung von die Variation der Flussdichte ($\Delta j$), die Variación de la concentración ($\Delta c$), die Distanz ($\Delta z$) und die Zeitdauer ($\Delta t$) ergibt sich zun chst die Gleichung:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
Der bergang zum infinitesimalen Grenzfall f hrt zur Differentialform, die dem zweiten Fickschen Gesetz entspricht. Diese l sst sich mit die Flussdichte ($j$), die Konzentration ($c$), die Position ($z$) und der Zeit ($t$) wie folgt darstellen:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 16183)
Im 19. Jahrhundert waren bereits verschiedene Transportph nomene bekannt, wie etwa die W rmeleitung, die 1822 von Fourier beschrieben wurde, die Hydrodynamik von Fl ssigkeiten, die aus den NavierStokes-Gleichungen hervorging, und biologische Prozesse wie die Osmose, bei denen man eine Bewegung von Stoffen ohne sichtbaren Fluss beobachten konnte.

Adolf Fick (18291901) [1]
Adolf Fick erkannte, dass sich die Massendiffusion zum Beispiel von Sauerstoff in Geweben hnlich wie die W rmeleitung verhielt. Im Jahr 1855, direkt inspiriert von Fouriers Gesetz, schlug Fick eine Analogie f r die Diffusion vor und formulierte das, was heute als sein erstes Gesetz bekannt ist, in dem der Massenfluss proportional zum Konzentrationsgradienten ist. Dieses Gesetz erm glichte es ihm, den Transport von Salz oder Gasen durch semipermeable Membranen und biologische Gewebe zu beschreiben. Sp ter kombinierte Fick dieses Gesetz mit dem Prinzip der Massenerhaltung, um zu untersuchen, wie sich die Konzentration im Laufe der Zeit ver ndert. So entstand das heute bekannte zweite Ficksche Gesetz, das die raum-zeitliche Entwicklung der Konzentration in einem diffusionsgesteuerten Medium beschreibt. Er wandte diese Gesetze vor allem auf die Analyse des Gastransports in Geweben an, insbesondere auf die Diffusion von Sauerstoff in der Hornhaut und von Salzen durch biologische Membranen.[1] Adolf Fick (1829-1901) vom Maler Anton Klamroth[2] " ber Diffusion" (1855), ver ffentlicht in den Annalen der Physik
(ID 16194)
Das allgemeine Ficksche Gesetz, das die Konzentration ($c$), die Diffusionskonstante ($D$), die Position ($z$) und der Zeit ($t$) umfasst, lautet:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
Wenn der Diffusionskoeffizient die Diffusionskonstante ($D$) konstant ist, vereinfacht sich diese Gleichung zu:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 16185)
Im Fall, dass die Diffusionskonstante ($D$) konstant ist, vereinfacht sich das allgemeine Gesetz von Fick und erlaubt es, die Konzentration ($c$) in Abh ngigkeit von die Position ($z$) und der Zeit ($t$) auszudr cken:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
Durch L sen dieser Gleichung erh lt man den folgenden analytischen Ausdruck:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 16186)
Die resultierende Verteilung f r die Konzentration ($c$) in Abh ngigkeit von die Diffusionskonstante ($D$), die Position ($z$) und der Zeit ($t$) ergibt sich zu:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
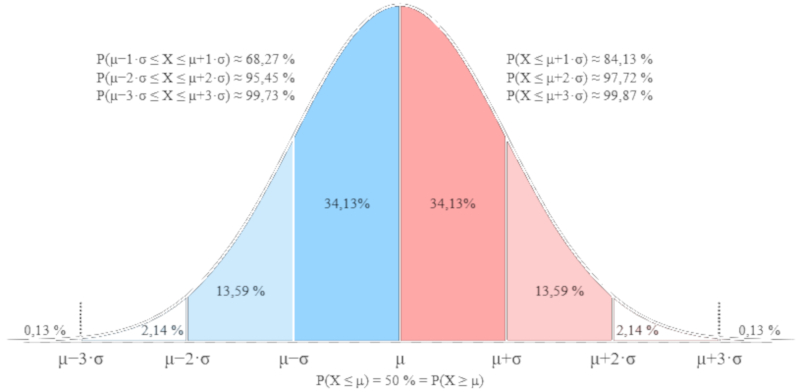
Dieser Ausdruck entspricht einer Gau schen Verteilung, die unten dargestellt ist:

(ID 12142)
Die Breite der Verteilung wird durch den Faktor die Standardabweichung ($\sigma$) bestimmt, der der Standardabweichung der Verteilung entspricht und sich als Quadratwurzel aus die Diffusionskonstante ($D$) und der Zeit ($t$) berechnen l sst, gem :
| $ \sigma =\sqrt{2 D t }$ |
Das bedeutet, dass die Breite mit der Quadratwurzel der Zeit w chst, w hrend die maximale H he umgekehrt proportional zu diesem Faktor abnimmt.
(ID 16188)
Die Konzentration ($c$) stellt eine Verteilung dar, die von die Diffusionskonstante ($D$) abh ngt und als Funktion von die Position ($z$) und der Zeit ($t$) ausgedr ckt wird:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Da der Zeit ($t$) ber die Standardabweichung ($\sigma$) mit die Diffusionskonstante ($D$) verkn pft ist, ergibt sich:
| $ \sigma =\sqrt{2 D t }$ |
woraus folgt:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16190)
Die Konzentration ($c$) wird von die Geschwindigkeit des Mediums ($u$) beeinflusst, das dem durch die Diffusionskonstante ($D$) beschriebenen Diffusionsprozess im positiven Bereich von die Position ($z$) entgegenwirkt und somit die Verteilung in der Zeit ($t$) gem folgender Gleichung ver ndert:
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
Im Fall einer konstanten die Geschwindigkeit des Mediums ($u$) ergibt sich die folgende L sung:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
dabei tritt die Fehlerfunktion erf, auch Gau sche Fehlerfunktion genannt, auf:
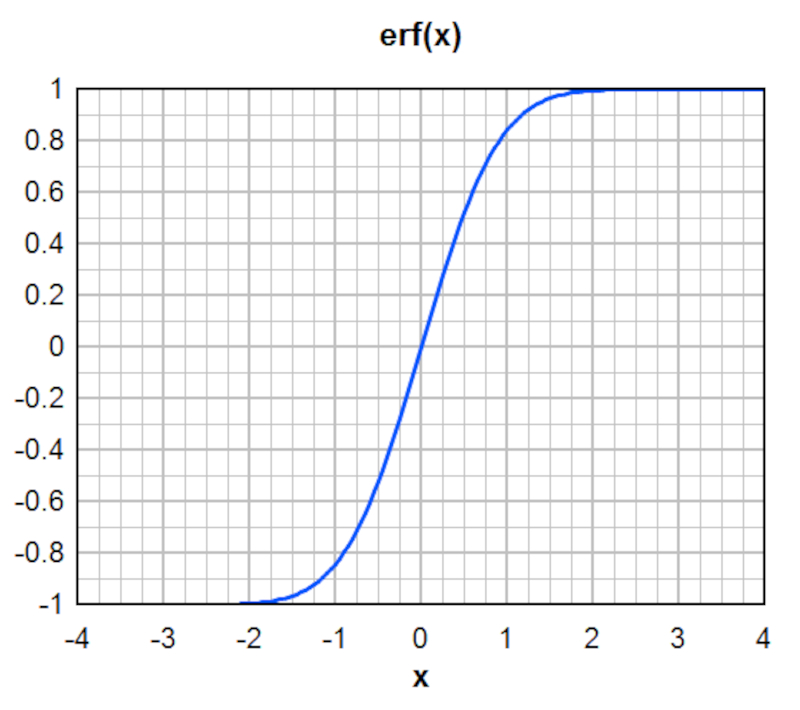
Diese L sung bedeutet, dass der Punkt, an dem die Konzentration die H lfte ihres Anfangswerts erreicht, sich mit der Flussgeschwindigkeit bewegt, gem :
$z = u t$
Au erdem flacht das Konzentrationsprofil mit der Zeit ab, da die Breite der bergangszone von der Standardabweichung abh ngt:
| $ \sigma =\sqrt{2 D t }$ |
(ID 16192)
(ID 16187)
ID:(1624, 0)
