Procesos de difusión
Storyboard 
El proceso básico de difusión permite entender como con el tiempo in homogeneidades de concentración tienden a desaparecer.
ID:(1624, 0)
Difusión
Imagen 
La difusión se origina por la diferencia de concentración de las partículas. Si otras palabras, al existir un numero mayor de partículas en una zona respecto de una segunda existe una mayor probabilidad que pase de esta a la segunda que a la inversa.

ID:(12139, 0)
Calculo de concentraciones
Imagen 
Para determinar la concentración en un punto se necesita calcular las cantidades que ingresan y las que salen de un volumen. Por ello para un espacio entre dos posición se considera el flujo que entra en restar lo que sale. Por ello la variación de la cantidad es igual a la concentración por el largo del segmento que es a su vez igual a el flujo por el tiempo considerado:
ID:(12141, 0)
Forma de la distribución
Imagen 
La distribución obtenida corresponde con concentración $1/m^3$, constante de difusión $m^2/s$, posición $m$ y tiempo $s$ a :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
que corresponde a una distribución de Gauss y que se muestra a continuación.
ID:(12142, 0)
Procesos de difusión
Modelo 
La difusión ocurre cuando hay una diferencia de concentración entre regiones, lo que provoca que las partículas se desplacen desde las zonas donde hay más hacia aquellas donde hay menos. El flujo resultante depende de qué tan grande es esa diferencia y de la distancia sobre la que ocurre. Al analizar cómo varía ese flujo entre dos puntos a lo largo del tiempo, se llega a una expresión que describe cómo cambia la concentración localmente. Cuando la velocidad de difusión es constante, esta expresión se simplifica y describe una distribución en forma de campana que cambia con el tiempo y el espacio. Dicha distribución se ensancha a medida que pasa el tiempo, mientras que su altura disminuye proporcionalmente.
Variables
Cálculos
Cálculos
Ecuaciones
La densidad de flujo ($j$) depende de la constante de difusión ($D$) y del gradiente, el cual se estima a partir de la variación de la concentración ($\Delta c$) y la distancia ($\Delta z$):
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
En el l mite en que se pasa de intervalos discretos a diferenciales infinitesimales ($\Delta z \rightarrow dz$), se obtiene para la concentración ($c$) y la posición ($z$):
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 12140)
La variación de la concentración ($\Delta c$) var a con la duración de tiempo ($\Delta t$) en funci n de la variación de la densidad de flujo ($\Delta j$), la cual a su vez depende de la distancia ($\Delta z$):
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
En el l mite en que se pasa de intervalos discretos a diferenciales infinitesimales ($\Delta z \rightarrow dz$, $\Delta t \rightarrow dt$), se obtiene para la concentración ($c$), la densidad de flujo ($j$), la posición ($z$) y el tiempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 12144)
La segunda ley de Fick establece que la variaci n de la concentración ($c$) con respecto a el tiempo ($t$) es igual a la variaci n de la densidad de flujo ($j$) con respecto a la posición ($z$):
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
que con la relaci n para la densidad de flujo ($j$)
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
resulta en la ecuaci n de difusi n
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
(ID 12145)
La segunda ley de Fick, que relaciona la concentración ($c$), la constante de difusión ($D$), la posición ($z$) y el tiempo ($t$), se expresa mediante la siguiente ecuaci n:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
En el caso en que la constante de difusión ($D$) sea constante, esta ecuaci n se simplifica a:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 12146)
La ecuaci n diferencial que rige el comportamiento de la concentración ($c$), en el caso en que la constante de difusión ($D$) es constante, se aplica en funci n de la posición ($z$) y el tiempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
cuya soluci n es:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 12147)
En el caso de difusi n con la constante de difusión ($D$) constante, la distribuci n de la concentración ($c$) en funci n de la posición ($z$) y el tiempo ($t$) toma la siguiente forma:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Al introducir la desviación estándar ($\sigma$) en la forma:
| $ \sigma =\sqrt{2 D t }$ |
la distribuci n puede reescribirse como:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16189)
La concentración ($c$) est influida por la velocidad del medio ($u$), la cual act a en oposici n al proceso de difusi n caracterizado por la constante de difusión ($D$) en la regi n positiva de la posición ($z$), modificando as la distribuci n de el tiempo ($t$) seg n:
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
La soluci n correspondiente a esta ecuaci n tiene la siguiente forma:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
(ID 16193)
Ejemplos
La difusi n se origina por diferencias en la concentraci n de part culas. En otras palabras, cuando hay m s part culas en una regi n que en otra, existe una mayor probabilidad de que se desplacen desde la zona de mayor concentraci n hacia la de menor concentraci n, que en sentido contrario.

(ID 12139)
En un l quido o gas pueden presentarse situaciones en las que la concentraci n de una determinada propiedad (como una sustancia, calor o cantidad de movimiento) no sea homog nea.
En tales casos, es m s probable que las part culas asociadas a dicha propiedad se desplacen desde la regi n de mayor concentraci n hacia la de menor concentraci n, simplemente por el hecho de haber m s part culas disponibles en la primera. Como consecuencia, el flujo depender tanto de la diferencia de concentraci n como de la distancia sobre la que ocurre ese cambio; es decir, depender del gradiente de concentraci n.
Si en un punto $z$ de una soluci n la concentraci n es $c(z)$ y en otro punto $z + \Delta z$ la concentraci n es $c(z + \Delta z)$, entonces seg n la variación de la concentración ($\Delta c$):
$\Delta c = c(z + \Delta z) - c(z)$
esto define un gradiente seg n la distancia ($\Delta z$):
$\displaystyle\frac{c(z + \Delta z) - c(z)}{\Delta z} = \displaystyle\frac{\Delta c}{\Delta z} \sim \displaystyle\frac{\partial c}{\partial z}$
De acuerdo con la densidad de flujo ($j$), el flujo ser proporcional a dicho gradiente, y la constante de proporcionalidad se denomina la constante de difusión ($D$).
Por lo tanto, se obtiene:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Esta expresi n corresponde a la primera ley de Fick.
(ID 16180)
Para obtener una expresi n del flujo en un punto y no un valor promedio, se considera el l mite infinitesimal de los diferenciales de flujo. En este caso, la densidad de flujo ($j$), en funci n de la constante de difusión ($D$), la variación de la concentración ($\Delta c$) y la distancia ($\Delta z$), se expresa como:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Este l mite conduce a la denominada primera ley de Fick, la cual, en su forma continua y escrita en t rminos de la concentración ($c$) y la posición ($z$), se expresa como:
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 16181)
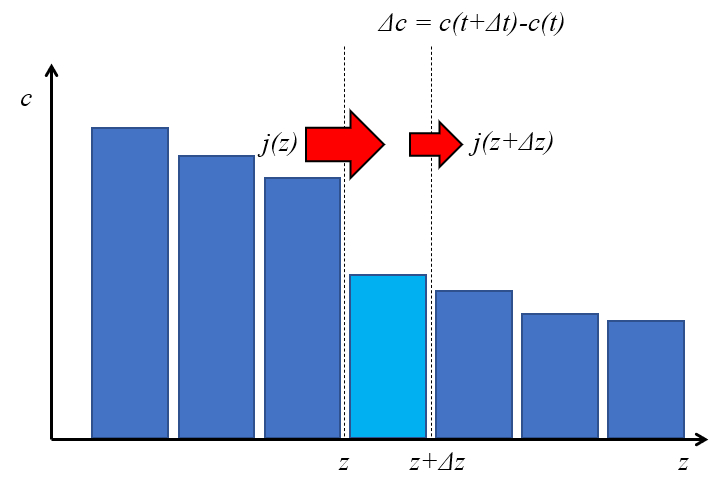
Para determinar la concentraci n en un punto, es necesario calcular las cantidades que ingresan y salen de un volumen de control. Por ello, en un espacio delimitado entre dos posiciones, se considera el flujo que entra menos el que sale. La variaci n de la cantidad contenida es entonces igual a la concentraci n multiplicada por la longitud del segmento, lo cual equivale al flujo neto por el intervalo de tiempo considerado.

(ID 12141)
Si se considera un elemento de la distancia ($\Delta z$) durante un intervalo de tiempo la duración de tiempo ($\Delta t$), se tiene, seg n la densidad de flujo ($j$):
• En la posici n $z$, ingresa un flujo de $j(z), \Delta t$
• En la posici n $z + \Delta z$, sale un flujo de $j(z + \Delta z), \Delta t$
De acuerdo con la variación de la densidad de flujo ($\Delta j$), la variaci n del contenido del elemento es $\Delta c, \Delta z$.
Por lo tanto, el balance de masas queda expresado como:
$ \Delta c, \Delta z = \left[-j(z) + j(z + \Delta z)\right] \Delta t = -\Delta j, \Delta t $
Esto conduce a la siguiente relaci n fundamental:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
(ID 16182)
Para obtener la concentraci n en un punto, es necesario pasar de la versi n promediada a su forma local. Utilizando la variación de la densidad de flujo ($\Delta j$), la variación de la concentración ($\Delta c$), la distancia ($\Delta z$) y la duración de tiempo ($\Delta t$), se parte de la ecuaci n:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
Al tomar el l mite infinitesimal, se obtiene la forma diferencial correspondiente a la segunda ley de Fick. Esta, en funci n de la densidad de flujo ($j$), la concentración ($c$), la posición ($z$) y el tiempo ($t$), se expresa como:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 16183)
En el siglo XIX ya se conoc an varios fen menos de transporte, como la conducci n del calor descrita por Fourier en 1822, la hidrodin mica de los fluidos desarrollada a partir de las ecuaciones de NavierStokes, y procesos biol gicos como la smosis, en los que se observaba movimiento de sustancias sin un flujo visible.

Adolf Fick (18291901) [1]
Adolf Fick not que la difusi n de masa, por ejemplo del ox geno en tejidos, parec a comportarse de forma similar a la conducci n del calor. En 1855, inspirado directamente por la ley de Fourier, Fick propuso una analog a para la difusi n, formulando lo que hoy se conoce como su primera ley, donde el flujo de masa es proporcional al gradiente de concentraci n. Esta ley le permiti describir el transporte de sal o gases a trav s de membranas semipermeables y tejidos biol gicos. Posteriormente, para estudiar c mo var a la concentraci n con el tiempo, Fick combin esta ley con el principio de conservaci n de masa, dando origen a lo que se conoce como la segunda ley de Fick, que describe la evoluci n espacio-temporal de la concentraci n en un medio difusivo. Aplic estas leyes principalmente al an lisis del transporte de gases en tejidos, en particular al estudio de la difusi n de ox geno en la c rnea y de sales a trav s de membranas biol gicas.[1] Adolf Fick (1829-1901) durch Maler Anton Klamroth (gest. 1929)[2] ber Diffusion (1855), publicada en los Annalen der Physik
(ID 16194)
La ley de Fick en su forma general, que involucra la concentración ($c$), la constante de difusión ($D$), la posición ($z$) y el tiempo ($t$), se expresa como:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
Cuando la constante de difusi n la constante de difusión ($D$) es constante, esta ecuaci n se simplifica a:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 16185)
En el caso en que la constante de difusión ($D$) sea constante, la ley general de Fick se simplifica y permite expresar la concentración ($c$) en funci n de la posición ($z$) y el tiempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
Al resolver esta ecuaci n, se obtiene la siguiente expresi n anal tica:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 16186)
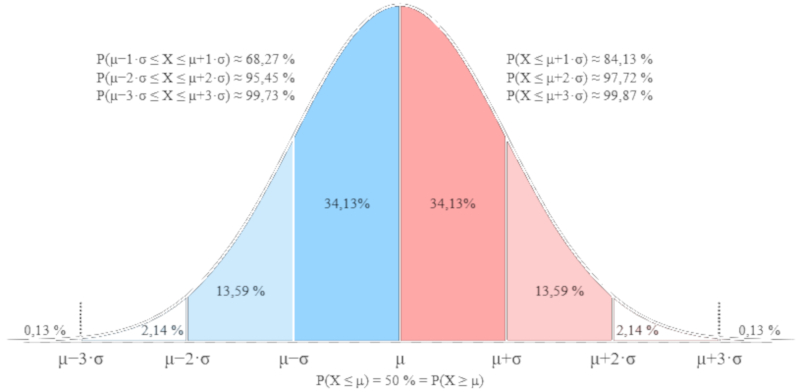
La distribuci n obtenida para la concentración ($c$), en funci n de la constante de difusión ($D$), la posición ($z$) y el tiempo ($t$), est dada por:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Esta expresi n corresponde a una distribuci n de Gauss, la cual se muestra a continuaci n:

(ID 12142)
El ancho de la distribuci n est determinado por el factor la desviación estándar ($\sigma$), que corresponde a la desviaci n est ndar de la distribuci n y puede calcularse como la ra z cuadrada de la constante de difusión ($D$) y el tiempo ($t$), seg n:
| $ \sigma =\sqrt{2 D t }$ |
Esto implica que el ancho de la distribuci n crece con la ra z del tiempo, mientras que la altura m xima disminuye en proporci n inversa a dicho factor.
(ID 16188)
La concentración ($c$) representa una distribuci n que depende de la constante de difusión ($D$) y se expresa como funci n de la posición ($z$) y el tiempo ($t$):
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Dado que el tiempo ($t$) se relaciona con la constante de difusión ($D$) a trav s de la desviación estándar ($\sigma$), mediante:
| $ \sigma =\sqrt{2 D t }$ |
se obtiene finalmente:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16190)
La concentración ($c$) est influida por la velocidad del medio ($u$), la cual act a en oposici n al proceso de difusi n descrito por la constante de difusión ($D$) en la regi n positiva de la posición ($z$), modificando as la distribuci n en el tiempo ($t$) seg n:
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
En el caso en que la velocidad del medio ($u$) sea constante, se obtiene la siguiente soluci n:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
donde aparece la funci n erf, o funci n error de Gauss:
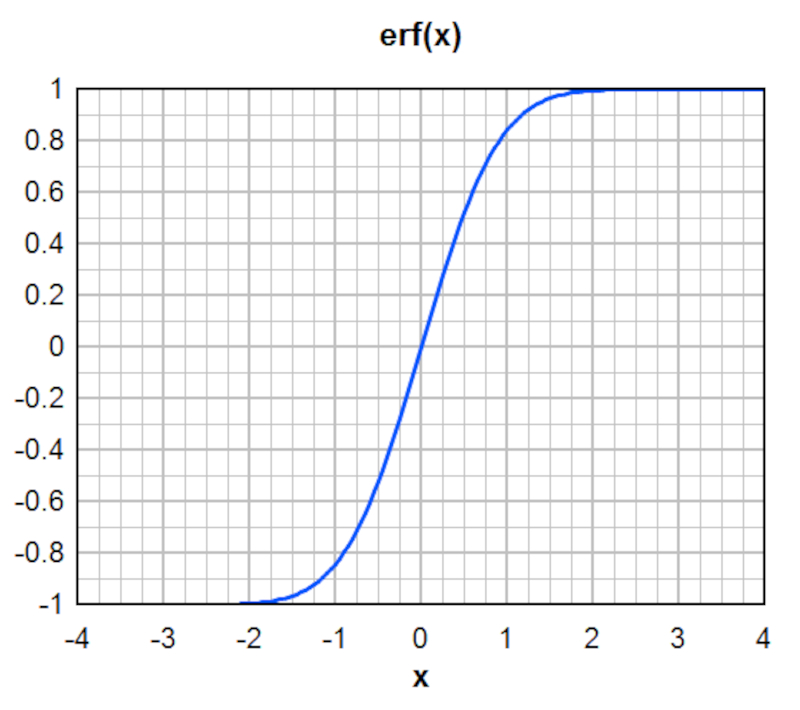
Esta soluci n implica que el punto donde la concentraci n alcanza la mitad de su valor inicial se desplaza en el tiempo con la velocidad del flujo, seg n:
$z = u t$
Adem s, el perfil de concentraci n se va aplanando con el tiempo, ya que el ancho de la zona en que var a la concentraci n depende de la desviaci n est ndar:
| $ \sigma =\sqrt{2 D t }$ |
(ID 16192)
(ID 16187)
ID:(1624, 0)
