Processos de difusão
Modelo 
A difusão ocorre quando há uma diferença de concentração entre regiões, fazendo com que as partículas se movam das áreas de maior concentração para as de menor concentração. O fluxo resultante depende da magnitude dessa diferença e da distância sobre a qual ela ocorre. Ao analisar como esse fluxo varia entre dois pontos ao longo do tempo, chega-se a uma expressão que descreve como a concentração muda localmente. Quando a taxa de difusão é constante, essa expressão se simplifica e descreve uma distribuição em forma de sino que evolui com o tempo e a posição. Essa distribuição se alarga com o tempo, enquanto a altura de seu pico diminui proporcionalmente.
Variáveis
Cálculos
Cálculos
Equações
La densidade de fluxo ($j$) depende de la constante de difusão ($D$) e do gradiente, o qual estimado a partir de ERROR:9080 e la distância ($\Delta z$):
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
No limite em que os intervalos discretos se tornam diferenciais infinitesimais ($\Delta z \rightarrow dz$), obt m-se para la concentração ($c$) e la posição ($z$):
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 12140)
ERROR:9080 varia com la duração do tempo ($\Delta t$) em fun o de la variação da densidade de fluxo ($\Delta j$), que por sua vez depende de la distância ($\Delta z$):
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
No limite em que os intervalos discretos se tornam diferenciais infinitesimais ($\Delta z \rightarrow dz$, $\Delta t \rightarrow dt$), obt m-se para la concentração ($c$), la densidade de fluxo ($j$), la posição ($z$) e o tempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 12144)
A segunda lei de Fick estabelece que a varia o de la concentração ($c$) em rela o a o tempo ($t$) igual varia o de la densidade de fluxo ($j$) em rela o a la posição ($z$):
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
com a rela o para la densidade de fluxo ($j$):
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
obt m-se ent o a equa o de difus o:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
(ID 12145)
A segunda lei de Fick, que relaciona la concentração ($c$), la constante de difusão ($D$), la posição ($z$) e o tempo ($t$), expressa da seguinte forma:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
No caso de la constante de difusão ($D$) ser constante, esta equa o se simplifica para:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 12146)
A equa o diferencial que descreve la concentração ($c$), no caso em que la constante de difusão ($D$) constante, expressa em fun o de la posição ($z$) e o tempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
cuja solu o :
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 12147)
No caso de difus o com la constante de difusão ($D$) constante, a distribui o de la concentração ($c$) em fun o de la posição ($z$) e o tempo ($t$) assume a seguinte forma:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Ao introduzir la desvio padrão ($\sigma$) na forma:
| $ \sigma =\sqrt{2 D t }$ |
a distribui o pode ser reescrita como:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16189)
La concentração ($c$) influenciada por la velocidade do meio ($u$), que atua contra o processo de difus o caracterizado por la constante de difusão ($D$) na regi o positiva de la posição ($z$), modificando assim a distribui o em o tempo ($t$) de acordo com:
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
A solu o dessa equa o tem a seguinte forma:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
(ID 16193)
Exemplos
A difus o ocorre devido a diferen as na concentra o de part culas. Em outras palavras, quando h mais part culas em uma regi o do que em outra, h uma maior probabilidade de que elas se movam da regi o de maior concentra o para a de menor concentra o, e n o o contr rio.

(ID 12139)
Em um l quido ou g s, podem ocorrer situa es em que a concentra o de uma determinada propriedade (como uma subst ncia, calor ou momento) n o homog nea.
Nessas condi es, as part culas associadas a essa propriedade tendem a se mover da regi o de maior concentra o para a de menor concentra o, simplesmente por haver mais part culas na primeira. Assim, o fluxo depende tanto da diferen a de concentra o quanto da dist ncia sobre a qual essa diferen a ocorre ou seja, depende do gradiente de concentra o.
Se a concentra o em um ponto $z$ de uma solu o for $c(z)$ e em outro ponto $z + \Delta z$ for $c(z + \Delta z)$, ent o, de acordo com ERROR:9080:
$\Delta c = c(z + \Delta z) - c(z)$
Isso define um gradiente conforme la distância ($\Delta z$):
$\displaystyle\frac{c(z + \Delta z) - c(z)}{\Delta z} = \displaystyle\frac{\Delta c}{\Delta z} \sim \displaystyle\frac{\partial c}{\partial z}$
Segundo la densidade de fluxo ($j$), o fluxo proporcional a esse gradiente, e a constante de proporcionalidade chamada de la constante de difusão ($D$).
Assim, obtemos:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Essa equa o conhecida como primeira lei de Fick.
(ID 16180)
Para obter uma express o do fluxo em um ponto e n o um valor m dio considera-se o limite infinitesimal dos diferenciais de fluxo. Nesse caso, la densidade de fluxo ($j$), em fun o de la constante de difusão ($D$), ERROR:9080 e la distância ($\Delta z$), expresso como:
| $ j = D \displaystyle\frac{\Delta c }{\Delta z }$ |
Esse limite leva chamada Primeira Lei de Fick, que, em sua forma cont nua e escrita em termos de la concentração ($c$) e la posição ($z$), dada por:
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
(ID 16181)
Para determinar a concentra o em um ponto, necess rio calcular as quantidades que entram e saem de um volume de controle. Assim, em um espa o delimitado entre duas posi es, considera-se o fluxo de entrada menos o fluxo de sa da. A varia o da quantidade contida ent o igual concentra o multiplicada pelo comprimento do segmento, o que equivale ao fluxo l quido vezes o intervalo de tempo considerado.
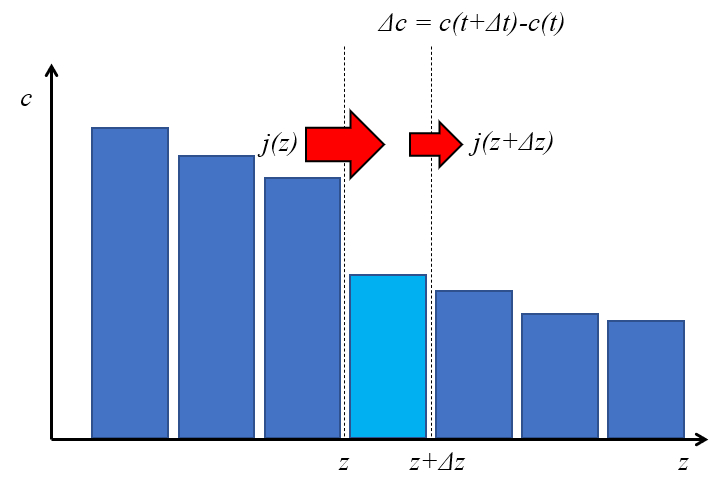
(ID 12141)
Considerando um elemento de la distância ($\Delta z$) durante um intervalo de tempo la duração do tempo ($\Delta t$), tem-se, de acordo com la densidade de fluxo ($j$):
• Na posi o $z$, entra um fluxo de $j(z), \Delta t$
• Na posi o $z + \Delta z$, sai um fluxo de $j(z + \Delta z), \Delta t$
Segundo la variação da densidade de fluxo ($\Delta j$), a varia o do conte do do elemento $\Delta c, \Delta z$.
Portanto, o balan o de massa expresso como:
$ \Delta c, \Delta z = \left[-j(z) + j(z + \Delta z)\right] \Delta t = -\Delta j, \Delta t $
Isso leva seguinte rela o fundamental:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
(ID 16182)
Para obter a concentra o em um ponto espec fico, necess rio passar da forma m dia para a forma local. Utilizando la variação da densidade de fluxo ($\Delta j$), ERROR:9080, la distância ($\Delta z$) e la duração do tempo ($\Delta t$), parte-se da seguinte equa o:
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
Ao tomar o limite infinitesimal, chega-se forma diferencial correspondente Segunda Lei de Fick. Esta, em fun o de la densidade de fluxo ($j$), la concentração ($c$), la posição ($z$) e o tempo ($t$), dada por:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
(ID 16183)
No s culo XIX, j eram conhecidos diversos fen menos de transporte, como a condu o de calor descrita por Fourier em 1822, a hidrodin mica dos fluidos desenvolvida a partir das equa es de NavierStokes, e processos biol gicos como a osmose, nos quais se observava o movimento de subst ncias sem fluxo vis vel.

Adolf Fick (18291901) [1]
Adolf Fick observou que a difus o de massa como, por exemplo, a do oxig nio nos tecidos parecia comportar-se de maneira semelhante condu o de calor. Em 1855, diretamente inspirado pela lei de Fourier, Fick prop s uma analogia para a difus o, formulando o que hoje conhecido como sua primeira lei, na qual o fluxo de massa proporcional ao gradiente de concentra o. Essa lei permitiu-lhe descrever o transporte de sal ou gases atrav s de membranas semiperme veis e tecidos biol gicos. Posteriormente, para estudar como a concentra o varia ao longo do tempo, Fick combinou essa lei com o princ pio da conserva o de massa, originando o que conhecido como a segunda lei de Fick, que descreve a evolu o espa o-temporal da concentra o em um meio difusivo. Ele aplicou essas leis principalmente an lise do transporte de gases em tecidos, em especial ao estudo da difus o de oxig nio na c rnea e de sais atrav s de membranas biol gicas.[1] Adolf Fick (1829-1901) pelo pintor Anton Klamroth[2] " ber Diffusion" (1855), publicado nos Annalen der Physik
(ID 16194)
A forma geral da lei de Fick, que envolve la concentração ($c$), la constante de difusão ($D$), la posição ($z$) e o tempo ($t$), dada por:
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
Quando o coeficiente de difus o la constante de difusão ($D$) constante, essa equa o se simplifica para:
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
(ID 16185)
No caso em que la constante de difusão ($D$) seja constante, a lei geral de Fick se simplifica e permite expressar la concentração ($c$) em fun o de la posição ($z$) e o tempo ($t$):
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
Ao resolver essa equa o, obt m-se a seguinte express o anal tica:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
(ID 16186)
A distribui o resultante de la concentração ($c$), em fun o de la constante de difusão ($D$), la posição ($z$) e o tempo ($t$), dada por:
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Essa express o corresponde a uma distribui o Gaussiana, representada a seguir:
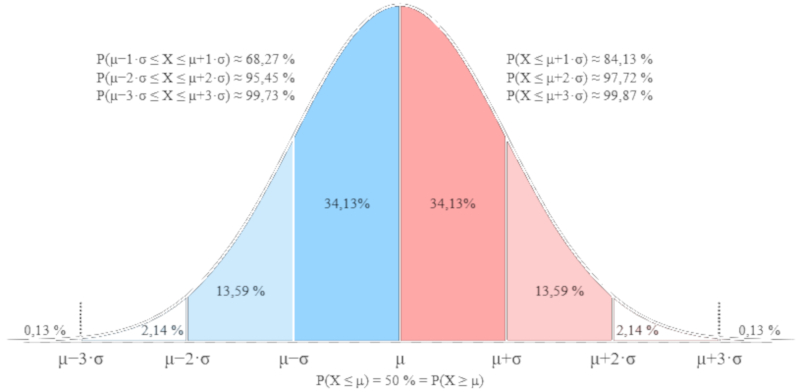
(ID 12142)
A largura da distribui o determinada pelo fator la desvio padrão ($\sigma$), que corresponde ao desvio padr o da distribui o e pode ser calculada como a raiz quadrada de la constante de difusão ($D$) e o tempo ($t$), de acordo com:
| $ \sigma =\sqrt{2 D t }$ |
Isso significa que a largura aumenta com a raiz quadrada do tempo, enquanto a altura central diminui proporcionalmente ao inverso desse fator.
(ID 16188)
La concentração ($c$) representa uma distribui o que depende de la constante de difusão ($D$) e expressa como uma fun o de la posição ($z$) e o tempo ($t$):
| $ c =\displaystyle\frac{1}{\sqrt{4\pi D t }} e^{- z ^2/4 D t }$ |
Como o tempo ($t$) est relacionada a la constante de difusão ($D$) por meio de la desvio padrão ($\sigma$), temos:
| $ \sigma =\sqrt{2 D t }$ |
o que leva a:
| $ c =\displaystyle\frac{1}{\sqrt{2\pi} \sigma } e^{- z ^2/2 \sigma ^2 }$ |
(ID 16190)
La concentração ($c$) influenciada por la velocidade do meio ($u$), que atua contra o processo de difus o descrito por la constante de difusão ($D$) na regi o positiva de la posição ($z$), modificando assim a distribui o em o tempo ($t$) de acordo com:
| $\displaystyle\frac{\partial c}{\partial t} + u \displaystyle\frac{\partial c}{\partial z} = D \displaystyle\frac{\partial^2 c}{\partial z ^2}$ |
No caso em que la velocidade do meio ($u$) seja constante, obt m-se a seguinte solu o:
| $ c = c_0 [1 - erf\left(\displaystyle\frac{ z - u t }{ 2\sqrt{ D t }}\right)]$ |
na qual aparece a fun o erf, ou fun o erro de Gauss:
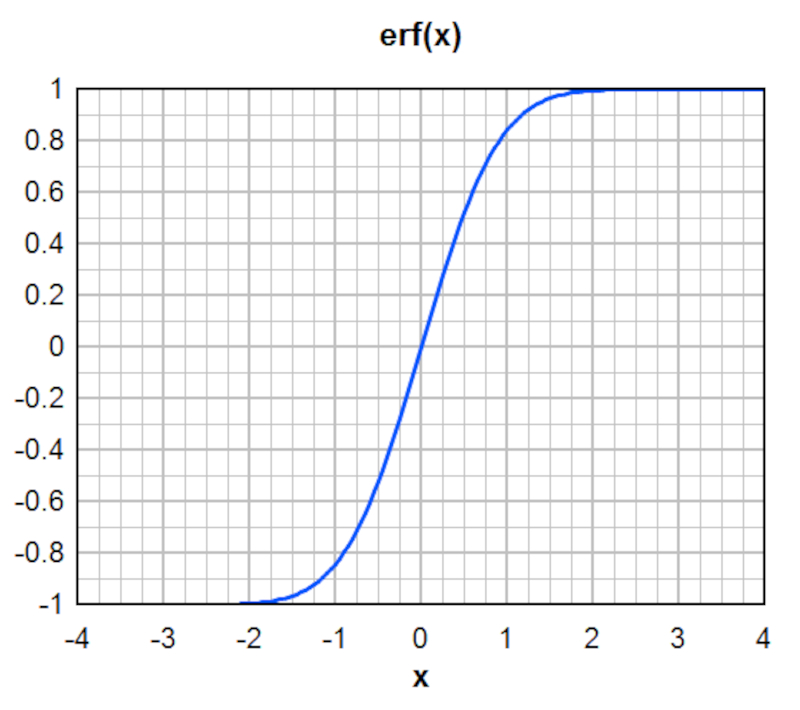
Essa solu o indica que o ponto onde a concentra o atinge metade de seu valor inicial se desloca ao longo do tempo com a velocidade do fluxo, segundo:
$z = u t$
Al m disso, o perfil de concentra o se torna mais suave com o tempo, pois a largura da zona de transi o depende do desvio padr o:
| $ \sigma =\sqrt{2 D t }$ |
(ID 16192)
(ID 16187)
ID:(1624, 0)
