User:
Measured compressibility coefficient for different salinities
Definition 
The compressibility coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:
In general, it is observed that compressibility:
- decreases with increasing salinity.
- decreases with increasing temperature.
ID:(11989, 0)
Concentration coefficient measured for different salinities
Image
The concentration coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:
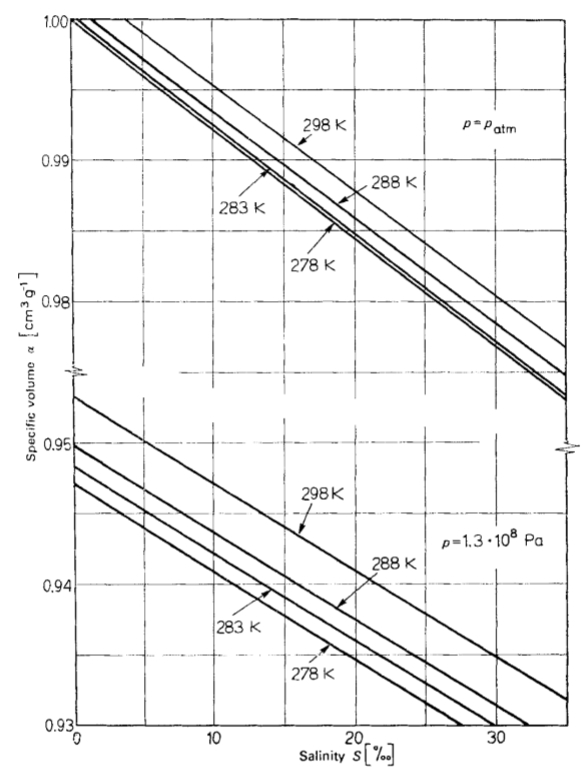
Two groups of curves can be observed, one at shallow depth ($1 atm$) and the other at high depth ($1.3\times 10^8 Pa$). The difference is that at greater depths, the specific volume is smaller.
For both cases, it is observed that the specific volume:
- decreases with increasing salinity.
- decreases with increasing temperature.
ID:(11990, 0)
Coeficiente de contracción halina
Storyboard
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
The negative sign reflects the fact that an increase in salinity leads to an increase in density. Since the specific volume is the inverse of density, an increase in density necessarily results in a decrease in specific volume.
the coeficiente de contracción halina ($k_i$) adopts a form analogous to the compresividad isotermica ($k_p$) and the thermic dilatation coefficient ($k_T$), according to how the volumen ($V$) varies with the salinidad ($i$), which is defined by:
In the oceanographic context, we use the volumen especifico ($\alpha$) instead of the volume ($V$), as defined by:
Therefore, the corresponding contraction coefficient should be expressed as follows:
Examples
Simulation of the volumetric contraction process due to salinity. When salt is added to water, the resulting volume decreases.
The coeficiente de contracción halina ($k_i$) adopts a form analogous to the compresividad isotermica ($k_p$) and the thermic dilatation coefficient ($k_T$), according to how the volumen ($V$) varies with the salinidad ($i$), which is defined by:
In the oceanographic context, we use the volumen especifico ($\alpha$) instead of the volume ($V$), as defined by:
Therefore, the corresponding contraction coefficient should be expressed as follows:
The compressibility coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:
In general, it is observed that compressibility:
- decreases with increasing salinity.
- decreases with increasing temperature.
The concentration coefficient for oceanic water, measured as a function of salinity, exhibits the trend shown in the following graph:
Two groups of curves can be observed, one at shallow depth ($1 atm$) and the other at high depth ($1.3\times 10^8 Pa$). The difference is that at greater depths, the specific volume is smaller.
For both cases, it is observed that the specific volume:
- decreases with increasing salinity.
- decreases with increasing temperature.
When salt is added to water, the total resulting volume is smaller than the sum of the individual volumes of the two components. In this sense, salt literally contracts water. Therefore, it is logical to define a the coeficiente de contracción halina ($k_i$) that compares the partial derivative of volume with respect to salinity at constant temperature and pressure ($\Delta V_{i,pT}$) with the volume Variation ($\Delta V$), in an analogous way to the variation in salinity ($\Delta i$), according to the following expression:
The typical value of this coefficient for ocean water ranges approximately between $6.5\times 10^{-4}$ and $8\times 10^{-4}$ 1/PSU, where PSU (Practical Salinity Units) corresponds to grams of salt per kilogram of water.
The challenge of working with volume in the case of seawater is that it depends on variations in temperature, salinity, and pressure. On the other hand, mass is less affected by these variations, which is why it makes sense to work with what we call specific volume, calculated by dividing the volume $V$ by the mass $M$:
$\displaystyle\frac{V}{M}$
However, $M/V$ represents density, so the specific volume is defined as:
The coeficiente de contracción halina ($k_i$) can be calculated as the ratio between the fraction the variation of specific volume due to changes in salinity ($\Delta\alpha_i$) and the volumen especifico ($\alpha$) relative to the salinidad ($i$), as follows:
ID:(1535, 0)