Measured coefficient of thermal expansion
Definition 
The thermal expansion coefficient for oceanic water, when measured, takes the form indicated in the following graph:
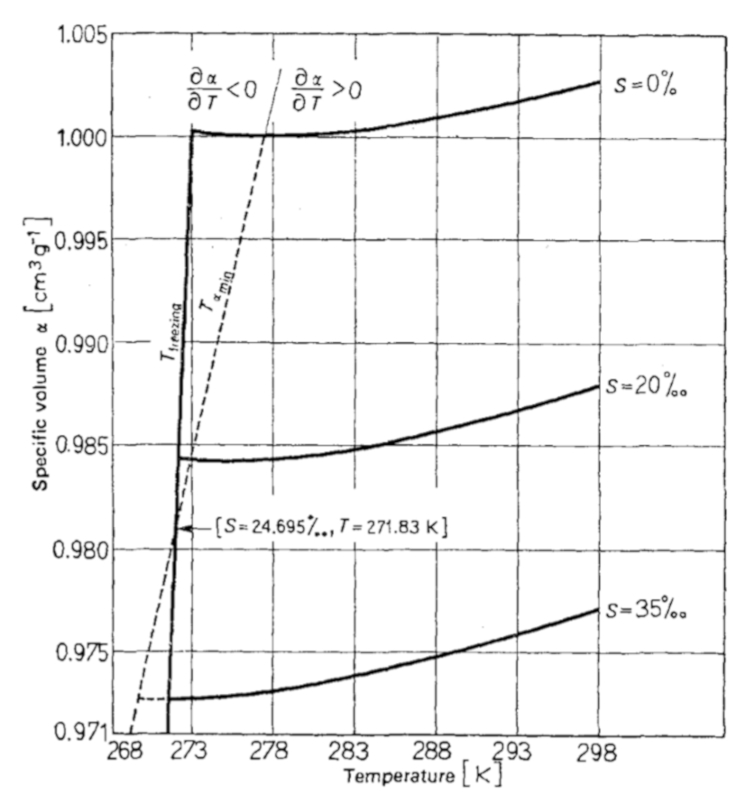
It is important to note that, depending on the salinity content, there is a range where the thermal expansion coefficient is negative:
For a salinity content greater than 24.695 ppt, there is a temperature range in which the thermal expansion coefficient is negative, meaning that as the temperature increases, the volume contracts.
ID:(11985, 0)
Causes sign change in coefficient of thermal expansion
Image 
The reason why the coefficient of thermal expansion has a range in which it is negative can be explained by the way molecules rearrange themselves when the temperature decreases before transitioning into the solid state. Between 273 K and 277 K, water molecules form chains that require more volume, which explains why the volume increases at lower temperatures.
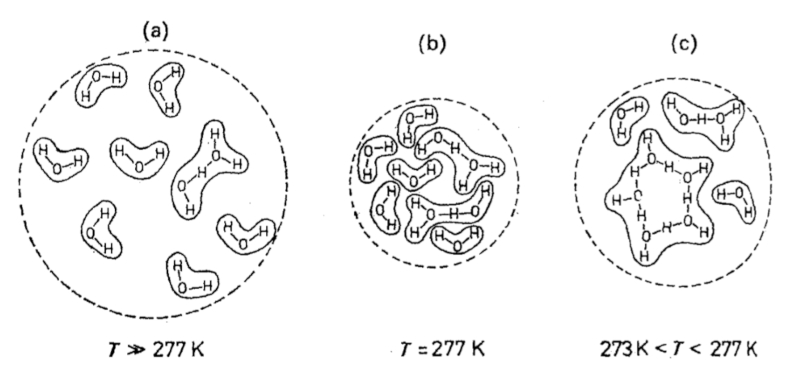
This image illustrates how water molecules arrange themselves into chains within this temperature range. As the temperature decreases, the molecules come closer together and form more stable bonds, resulting in an expansion of volume. However, once the temperature drops sufficiently and the water solidifies, the molecules pack into a more ordered crystalline structure, leading to a decrease in volume.
This phenomenon is known as the "anomaly of water" and is a unique characteristic of this compound. The detailed explanation of this behavior involves concepts such as the molecular structure of water and the formation of hydrogen bonds, which are essential to understanding why the coefficient of thermal expansion of water exhibits this negative temperature range.
In summary, the range in which the coefficient of thermal expansion of water is negative is due to the way water molecules reorganize and form chains at low temperatures, resulting in an increase in volume. This explanation is supported by an understanding of the molecular structure and hydrogen bonding present in water.
ID:(11986, 0)
Thermal expansion coefficient table
Note 
The coefficients of thermal expansion as a function of temperature and salinity are listed below:
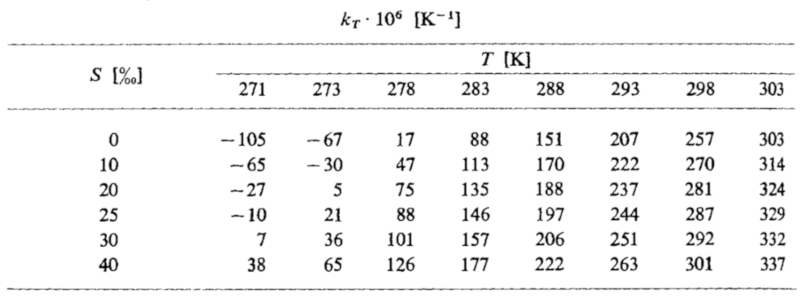
ID:(11987, 0)
Thermal Expansion
Description 
Variables
Calculations
Calculations
Equations
The thermal expansion coefficient is defined by
| $ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $ |
In the case of oceanic water, we work with the specific volume
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
instead of the volume $V$. Therefore, a change of variable can be made, resulting in the thermal expansion coefficient as
| $ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$ |
.
(ID 11980)
Examples
Simulation of the volumetric expansion process induced by temperature. As the water heats up, the resulting volume expands.
(ID 16229)
The thermal expansion coefficient for oceanic water, when measured, takes the form indicated in the following graph:

It is important to note that, depending on the salinity content, there is a range where the thermal expansion coefficient is negative:
For a salinity content greater than 24.695 ppt, there is a temperature range in which the thermal expansion coefficient is negative, meaning that as the temperature increases, the volume contracts.
(ID 11985)
The reason why the coefficient of thermal expansion has a range in which it is negative can be explained by the way molecules rearrange themselves when the temperature decreases before transitioning into the solid state. Between 273 K and 277 K, water molecules form chains that require more volume, which explains why the volume increases at lower temperatures.

This image illustrates how water molecules arrange themselves into chains within this temperature range. As the temperature decreases, the molecules come closer together and form more stable bonds, resulting in an expansion of volume. However, once the temperature drops sufficiently and the water solidifies, the molecules pack into a more ordered crystalline structure, leading to a decrease in volume.
This phenomenon is known as the "anomaly of water" and is a unique characteristic of this compound. The detailed explanation of this behavior involves concepts such as the molecular structure of water and the formation of hydrogen bonds, which are essential to understanding why the coefficient of thermal expansion of water exhibits this negative temperature range.
In summary, the range in which the coefficient of thermal expansion of water is negative is due to the way water molecules reorganize and form chains at low temperatures, resulting in an increase in volume. This explanation is supported by an understanding of the molecular structure and hydrogen bonding present in water.
(ID 11986)
The coefficients of thermal expansion as a function of temperature and salinity are listed below:

(ID 11987)
The challenge of working with volume in the case of seawater is that it depends on variations in temperature, salinity, and pressure. On the other hand, mass is less affected by these variations, which is why it makes sense to work with what we call specific volume, calculated by dividing the volume $V$ by the mass $M$:
$\displaystyle\frac{V}{M}$
However, $M/V$ represents density, so the specific volume is defined as:
| $ \alpha = \displaystyle\frac{1}{ \rho }$ |
(ID 11984)
Thermal expansion, denoted by $\alpha$, can be defined as the ratio of the volume change $\Delta V/V$ to the temperature increase $\Delta T$. Mathematically, it can be expressed as:
| $ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $ |
The positive sign is associated with the fact that an increase in temperature $\Delta T > 0$ leads to an expansion of volume $\Delta V > 0$.
(ID 211)
In the case of the ocean, the concept of specific volume $\alpha$ is used instead of the thermal expansion coefficient $k_T$. Therefore, it is necessary to convert the thermal expansion coefficient, which is typically defined in terms of volume change, into terms of specific volume change. Thus, for a temperature variation $T$, the thermal expansion coefficient in terms of specific volume $\alpha$ can be expressed as follows:
| $ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$ |
(ID 11980)
ID:(1533, 0)
