Utilisateur:
Vagues déferlantes
Storyboard 
Les courants d'air au-dessus de l'océan entraînent le mouvement de l'eau, générant des vagues qui se comportent différemment en fonction des fluctuations de profondeur. Ce phénomène est connu sous le nom de déferlement des vagues. Le déferlement se produit parce que la vitesse de propagation d'une vague est plus grande dans les zones de plus grande profondeur. Ainsi, à mesure que les vagues approchent du rivage, celles provenant de zones plus profondes tendent à dépasser celles des zones moins profondes, entraînant le déferlement caractéristique des vagues.
ID:(1632, 0)
Mécanismes
Iframe
Mécanismes
ID:(15639, 0)
Casse de la vague sur la plage
Description
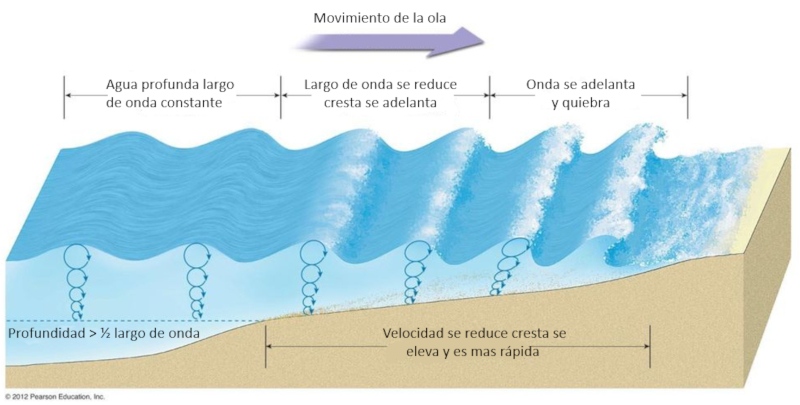
Lorsqu\'une vague atteint la plage, elle commence à monter sur la pente de la plage, devenant de plus en plus peu profonde et donc plus lente. Une deuxième vague qui la suit a tendance à se surélever par rapport à celle qui la précède. Comme l\'eau devient plus profonde dans cette situation, la deuxième vague est plus rapide et a tendance à dépasser l\'eau qui est arrivée en premier sur la plage. Cela conduit finalement à la formation de la déferlante.
ID:(12308, 0)
Fréquence angulaire
Concept
Rappelant que la vitesse angulaire représente l'angle parcouru par unité de temps, on peut observer que l'expression
$\displaystyle\frac{2\pi}{T}$
correspond à un tour complet ($2\pi$) divisé par le temps a période ($T$), nécessaire pour un cycle. Par conséquent, a fréquence angulaire ($\omega$) est défini comme
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(15648, 0)
Vecteur d'onde
Concept
Le vecteur de vague ($k$) est le facteur qui multiplie la position et correspond à la valeur pour laquelle, si l'onde se déplace le long de un longueur d'onde ($\lambda$), elle reprend la forme initiale qu'elle avait. Pour que cela se produise, la condition suivante doit être remplie :
$kx = k\lambda = 2\pi$
Par conséquent, avec le longueur d'onde ($\lambda$), nous établissons que :
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(15647, 0)
Vitesse de phase d'onde
Concept
La vitesse des vagues dépend de la profondeur de l'eau et du facteur le vecteur de vague ($k$), qui est calculé en utilisant le longueur d'onde ($\lambda$) comme suit :
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Concernant le vitesse des phases ($c_p$), qui correspond à la vitesse à laquelle chaque crête de vague se déplace, cela peut être déterminé en utilisant le profondeur de l'océan ($h$) et a accélération gravitationnelle ($g$). Le vitesse des phases ($c_p$) est calculé comme suit :
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
La vitesse de phase correspond à la vitesse à laquelle une oscillation ou une vague spécifique se déplace.
ID:(15649, 0)
Vitesse de groupe d'ondes
Concept
Les vagues ont une vitesse qui dépend de la profondeur de l'eau et du facteur le vecteur de vague ($k$), calculée en utilisant le longueur d'onde ($\lambda$) comme suit :
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Pour le vitesse de groupe ($c_g$), qui représente la vitesse à laquelle l'ensemble du train de vagues se déplace, et non chaque vague individuellement, elle peut être calculée en utilisant le vitesse des phases ($c_p$). Ce dernier est déterminé avec le profondeur de l'océan ($h$) et a accélération gravitationnelle ($g$), de la manière suivante :
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
Finalement, en utilisant ces informations, le vitesse de groupe ($c_g$) peut être calculé par l'expression suivante :
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
La vitesse de groupe est la vitesse à laquelle le train ou le groupe de vagues se déplace dans le milieu aquatique.
ID:(15650, 0)
Vitesses des vagues
Image
Il existe deux vitesses caractéristiques en mécanique des ondes. D'une part, il y a la vitesse à laquelle une onde spécifique se déplace, qui peut varier en fonction de la fréquence, différenciant ainsi une onde d'une autre.
Le second type de vitesse observé est celui d'un paquet d'ondes, c'est-à-dire un groupe d'ondes de différentes fréquences et phases qui, en se superposant, forment un groupe qui se déplace comme une unité. Cette vitesse est connue sous le nom de vitesse de groupe.
Ces deux vitesses peuvent être observées dans cette animation :
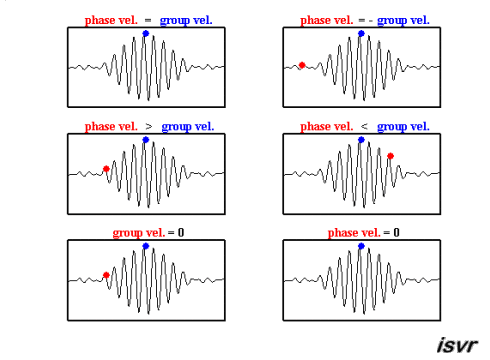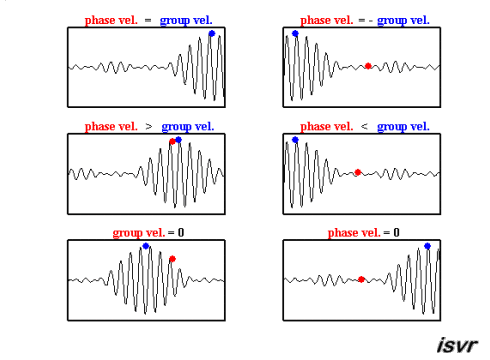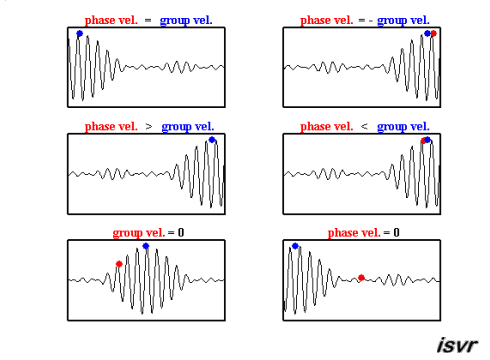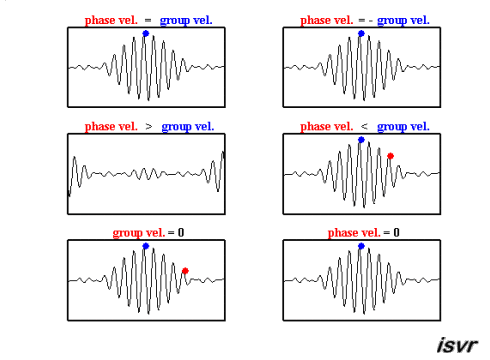
ID:(15651, 0)
Description de la vague
Concept
Une vague peut être approximativement décrite comme une fonction sinusoïdale en fonction des variables le position ($x$) et le temps ($t$).
La fonction intègre les valeurs de le hauteur des vagues ($z$) à chaque point, ainsi que le hauteur maximale des vagues ($z_0$), le vecteur de vague ($k$) et ($$) :
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(15646, 0)
Modèle
Top
Calculs
Variables
Paramètres
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser Équation
$ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$
c_g = c_p*(1 + 2* k * h / sinh( 2 * k * h ))/2
$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$
c_p =sqrt( g * tanh( k * h ) / k )
$ k =\displaystyle\frac{2 \pi }{ \lambda }$
k = 2* pi / lambda
$ \omega = \displaystyle\frac{2 \pi }{ T }$
omega = 2* pi / T
$ z ( x , t ) = z_0 sin( k x - \omega t )$
z_xt = z_0 *sin( k * x - omega * t )
ID:(15644, 0)
Description de la vague
Équation
Une vague peut être approximativement décrite comme une fonction sinusoïdale en fonction des variables le position ($x$) et le temps ($t$).
La fonction intègre les valeurs de le hauteur des vagues ($z$) à chaque point, ainsi que le hauteur maximale des vagues ($z_0$), le vecteur de vague ($k$) et ($$) :
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(12307, 0)
Vecteur d'onde
Équation
Le vecteur de vague ($k$) est avec le longueur d'onde ($\lambda$) égal à :
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(12309, 0)
Fréquence angulaire
Équation
A fréquence angulaire ($\omega$) est avec a période ($T$) égal à
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(12335, 0)
Vitesse de phase d'onde
Équation
Le vitesse des phases ($c_p$) correspond à la vitesse à laquelle chaque crête de vague se déplace, qui peut être déterminée en utilisant les valeurs de le profondeur de l'océan ($h$), le longueur d'onde ($\lambda$) et a accélération gravitationnelle ($g$). La vitesse le vitesse des phases ($c_p$) est calculée de la manière suivante :
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
ID:(12305, 0)
Vitesse de groupe d'ondes
Équation
Le vitesse de groupe ($c_g$) est calculé en utilisant les valeurs de le vecteur de vague ($k$), le profondeur de l'océan ($h$) et a accélération gravitationnelle ($g$) de la manière suivante :
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
ID:(12304, 0)