Modèle surfacique
Storyboard 
Le transfert de particules ou de molécules, telles que le CO2, entre l'atmosphère et l'océan implique un mécanisme plus complexe. Ce processus est associé à la formation d'un film liquide saturé de particules ou de molécules, qui régule le passage de nouvelles particules vers ou depuis l'intérieur de l'océan.
ID:(1633, 0)
Couche de surface
Image 
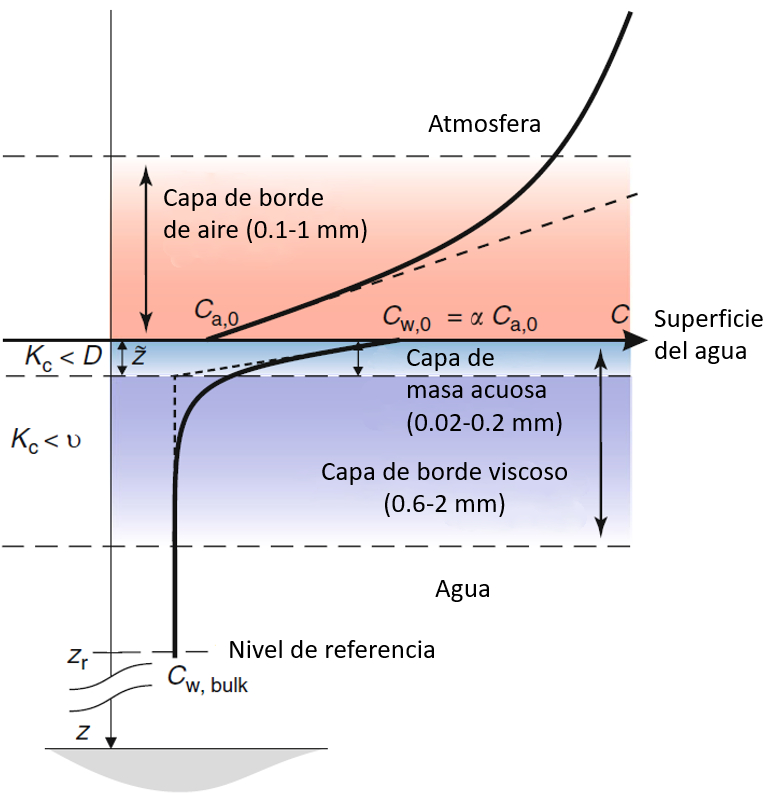
Pour étudier le transfert de CO2 à la surface de l'océan, il est nécessaire d\'observer attentivement les variations de concentration à la fois dans l\'air et dans l\'eau.
Dans l\'air, le CO2 pénètre dans l\'eau, créant une zone de faible concentration où il diminue de $C_a$ à $C_{a,0}$. Cette couche a une épaisseur de 0,1 à 1 mm.
Le CO2 qui pénètre dans l\'eau s\'accumule initialement à la surface, créant une concentration $C_{w,0}$, qui se diffuse ensuite vers l\'intérieur, atteignant une concentration plus faible $C_w$.
La réduction de la concentration permet de définir deux zones : une zone très mince, de 0,02 à 0,2 mm, où la concentration diminue rapidement, et une seconde zone, de 0,6 à 2 mm, où la concentration diminue plus progressivement jusqu\'à atteindre la concentration dans l\'eau.
ID:(12244, 0)
Échange de CO2, vitesse de l'eau
Noter 
A taux de transfert de gaz dans l'eau ($k_w$) peut être modélisé en utilisant des données mesurées. Tout d'abord, il dépend de la vitesse à laquelle le système élimine le carbone de l'interface air-eau, ce qui rend la vitesse de transport proportionnelle à la vitesse relative entre les deux milieux.
Deuxièmement, il y a un effet de la mobilité des ions, qui peut être décrit par le numéro de Schmidt ($Sc$), représentant la relation entre la diffusion de l'impulsion et les particules. Cependant, cette dépendance n'est pas linéaire et est influencée par un facteur ERROR:9926 qui varie entre -1/2 et -2/3 en fonction de la rugosité de la surface.
Enfin, a taux de transfert de gaz dans l'eau ($k_w$) dépend également de ERROR:9409, qui est à son tour déterminé par le niveau de rugosité de la surface.
En résumé, le gaz a taux de transfert de gaz dans l'eau ($k_w$) est décrit en fonction de ERROR:9437, ERROR:9408, le numéro de Schmidt ($Sc$), ERROR:9409 et ERROR:9926 de la manière suivante :
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Solubilité en fonction du nombre de Schmidt
Citation 
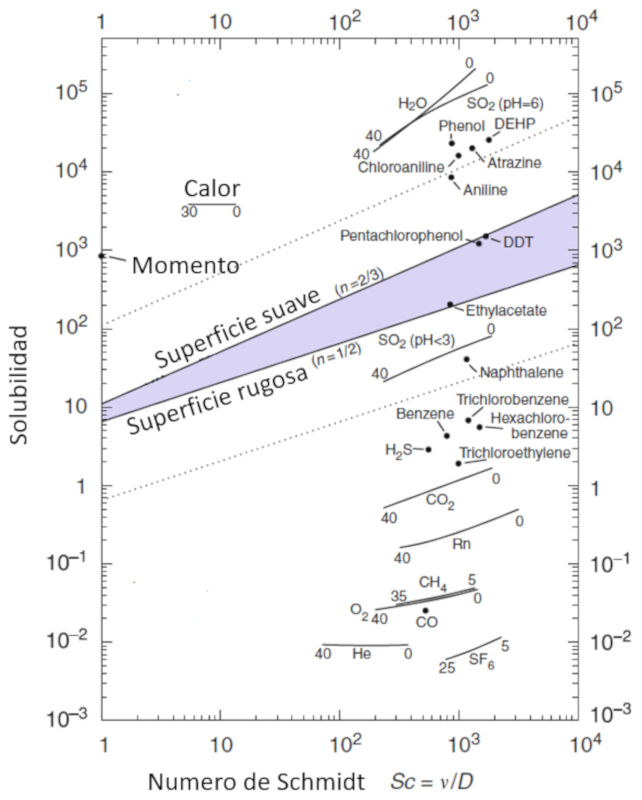
La mobilité des molécules, représentée par a solubilité du gaz ($\alpha$), est une fonction de la concentration de particules, décrite par le numéro de Schmidt ($Sc$), qui à son tour est calculée à partir de ERROR:9412, ERROR:9413 et ERROR:9414 selon l'équation suivante :
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Cette relation est illustrée dans le schéma suivant :
ID:(12245, 0)
Vitesse de transfert
Exercer 
A taux de transfert de gaz dans l'air ($k_a$) peut être estimé à partir de la loi de Fick, en comparant ERROR:9414 avec ERROR:9430 de la manière suivante :
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Vitesse de transfert et résistances
Équation 
Pour l'interaction entre l'atmosphère et l'océan, a résistance au transfert air-eau d'un gaz ($R_{ta}$) comprend initialement a résistance au transfert dans l'eau ($R_w$), suivi du processus d'évaporation $1/\alpha$ avec a solubilité du gaz ($\alpha$), et une fois que le gaz est passé dans l'air, a résistance de transfert dans l'air ($R_a$) agit sur lui :
Quant à l'interaction entre l'atmosphère et l'océan, a résistance au transfert eau-air d'un gaz ($R_{tw}$) comprend initialement a résistance de transfert dans l'air ($R_a$), suivi de a solubilité du gaz ($\alpha$), et une fois que le gaz a pénétré dans l'eau, a résistance au transfert dans l'eau ($R_w$) agit :
Avec ces équations, nous pouvons formuler les équations pour les vitesses de transfert.
Ainsi, en utilisant a taux de transfert total de gaz dans l'air ($k_{ta}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous établissons la relation suivante :
D'autre part, avec a taux de transfert total de gaz dans l'eau ($k_{tw}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous établissons que :
ID:(15654, 0)
Modèle surfacique
Storyboard 
Le transfert de particules ou de molécules, telles que le CO2, entre l'atmosphère et l'océan implique un mécanisme plus complexe. Ce processus est associé à la formation d'un film liquide saturé de particules ou de molécules, qui régule le passage de nouvelles particules vers ou depuis l'intérieur de l'océan.
Variables
Calculs
Calculs
Équations
La relation impliquant a résistance au transfert air-eau d'un gaz ($R_{ta}$), d termin e par la combinaison de a résistance au transfert dans l'eau ($R_w$), a résistance de transfert dans l'air ($R_a$) et a solubilité du gaz ($\alpha$), est formul e dans l' quation :
Cela inclut la relation de a résistance de transfert dans l'air ($R_a$) avec a taux de transfert de gaz dans l'air ($k_a$) exprim e dans :
De plus, l'interaction de a résistance au transfert dans l'eau ($R_w$) avec a taux de transfert de gaz dans l'eau ($k_w$) est expliqu e dans :
Et la connexion entre a résistance au transfert air-eau d'un gaz ($R_{ta}$) et a taux de transfert total de gaz dans l'air ($k_{ta}$) est sp cifi e dans :
Ces l ments ensemble fournissent la base pour d finir la relation pour a taux de transfert total de gaz dans l'air ($k_{ta}$) :
La relation entre a résistance au transfert eau-air d'un gaz ($R_{tw}$), tablie par les sommes de a résistance au transfert dans l'eau ($R_w$), a résistance de transfert dans l'air ($R_a$) et a solubilité du gaz ($\alpha$), est exprim e dans l' quation :
Incluant la relation de a résistance de transfert dans l'air ($R_a$) avec a taux de transfert de gaz dans l'air ($k_a$) dans :
L'interaction de a résistance au transfert dans l'eau ($R_w$) avec a taux de transfert de gaz dans l'eau ($k_w$) est d crite dans :
Et la connexion entre a résistance au transfert eau-air d'un gaz ($R_{tw}$) et a taux de transfert total de gaz dans l'eau ($k_{tw}$) est d taill e dans :
Ceci fournit la base pour tablir la relation pour a taux de transfert total de gaz dans l'eau ($k_{tw}$) :
Exemples
Pour tudier le transfert de CO2 la surface de l'oc an, il est n cessaire d\'observer attentivement les variations de concentration la fois dans l\'air et dans l\'eau.
Dans l\'air, le CO2 p n tre dans l\'eau, cr ant une zone de faible concentration o il diminue de $C_a$ $C_{a,0}$. Cette couche a une paisseur de 0,1 1 mm.
Le CO2 qui p n tre dans l\'eau s\'accumule initialement la surface, cr ant une concentration $C_{w,0}$, qui se diffuse ensuite vers l\'int rieur, atteignant une concentration plus faible $C_w$.
La r duction de la concentration permet de d finir deux zones : une zone tr s mince, de 0,02 0,2 mm, o la concentration diminue rapidement, et une seconde zone, de 0,6 2 mm, o la concentration diminue plus progressivement jusqu\' atteindre la concentration dans l\'eau.
A taux de transfert de gaz dans l'eau ($k_w$) peut tre mod lis en utilisant des donn es mesur es. Tout d'abord, il d pend de la vitesse laquelle le syst me limine le carbone de l'interface air-eau, ce qui rend la vitesse de transport proportionnelle la vitesse relative entre les deux milieux.
Deuxi mement, il y a un effet de la mobilit des ions, qui peut tre d crit par le numéro de Schmidt ($Sc$), repr sentant la relation entre la diffusion de l'impulsion et les particules. Cependant, cette d pendance n'est pas lin aire et est influenc e par un facteur ERROR:9926 qui varie entre -1/2 et -2/3 en fonction de la rugosit de la surface.
Enfin, a taux de transfert de gaz dans l'eau ($k_w$) d pend galement de ERROR:9409, qui est son tour d termin par le niveau de rugosit de la surface.
En r sum , le gaz a taux de transfert de gaz dans l'eau ($k_w$) est d crit en fonction de ERROR:9437, ERROR:9408, le numéro de Schmidt ($Sc$), ERROR:9409 et ERROR:9926 de la mani re suivante :
La mobilit des mol cules, repr sent e par a solubilité du gaz ($\alpha$), est une fonction de la concentration de particules, d crite par le numéro de Schmidt ($Sc$), qui son tour est calcul e partir de ERROR:9412, ERROR:9413 et ERROR:9414 selon l' quation suivante :
Cette relation est illustr e dans le sch ma suivant :
A taux de transfert de gaz dans l'air ($k_a$) peut tre estim partir de la loi de Fick, en comparant ERROR:9414 avec ERROR:9430 de la mani re suivante :
Pour l'interaction entre l'atmosph re et l'oc an, a résistance au transfert air-eau d'un gaz ($R_{ta}$) comprend initialement a résistance au transfert dans l'eau ($R_w$), suivi du processus d' vaporation $1/\alpha$ avec a solubilité du gaz ($\alpha$), et une fois que le gaz est pass dans l'air, a résistance de transfert dans l'air ($R_a$) agit sur lui :
Quant l'interaction entre l'atmosph re et l'oc an, a résistance au transfert eau-air d'un gaz ($R_{tw}$) comprend initialement a résistance de transfert dans l'air ($R_a$), suivi de a solubilité du gaz ($\alpha$), et une fois que le gaz a p n tr dans l'eau, a résistance au transfert dans l'eau ($R_w$) agit :
Avec ces quations, nous pouvons formuler les quations pour les vitesses de transfert.
Ainsi, en utilisant a taux de transfert total de gaz dans l'air ($k_{ta}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous tablissons la relation suivante :
D'autre part, avec a taux de transfert total de gaz dans l'eau ($k_{tw}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous tablissons que :
Le gradient de concentration entre a concentration de gaz dans l'atmosphère ($C_{a,0}$) et a concentration de gaz dans l'eau ($C_{w,0}$) d pend de a solubilité du gaz ($\alpha$). Par cons quent, la relation suivante est tablie :
A taux de transfert de gaz dans l'air ($k_a$) peut tre estim partir de la loi de Fick, en comparant ERROR:9414 avec ERROR:9430 de la mani re suivante :
Le param tre du gaz a taux de transfert de gaz dans l'eau ($k_w$) est d crit en fonction de ERROR:9437, ERROR:9408, le numéro de Schmidt ($Sc$), ERROR:9409 et ERROR:9926 comme suit :
A résistance de transfert dans l'air ($R_a$) est d fini comme l'inverse de a taux de transfert de gaz dans l'air ($k_a$). Cette relation peut tre exprim e de la mani re suivante :
A résistance au transfert dans l'eau ($R_w$) est d fini comme l'inverse de a taux de transfert de gaz dans l'eau ($k_w$). Cette relation peut tre exprim e de la mani re suivante :
A résistance au transfert eau-air d'un gaz ($R_{tw}$) est d fini comme l'inverse de a taux de transfert total de gaz dans l'eau ($k_{tw}$). Cette relation peut tre exprim e de la mani re suivante :
A résistance au transfert air-eau d'un gaz ($R_{ta}$) est d fini comme l'inverse de a taux de transfert total de gaz dans l'air ($k_{ta}$). Cette relation peut tre exprim e de la mani re suivante :
Pour l'interaction entre l'atmosph re et l'oc an, a résistance au transfert air-eau d'un gaz ($R_{ta}$) inclut d'abord a résistance au transfert dans l'eau ($R_w$), suivi par le processus d' vaporation $1/\alpha$ avec a solubilité du gaz ($\alpha$). Une fois que le gaz est pass dans l'air, a résistance de transfert dans l'air ($R_a$) agit sur lui :
Pour l'interaction entre l'atmosph re et l'oc an, a résistance au transfert eau-air d'un gaz ($R_{tw}$) inclut d'abord a résistance de transfert dans l'air ($R_a$), suivi par a solubilité du gaz ($\alpha$). Une fois que le gaz a p n tr dans l'eau, a résistance au transfert dans l'eau ($R_w$) agit :
La relation entre la r sistance au transfert entre l'atmosph re et l'oc an peut tre exprim e en termes des vitesses de transfert dans les deux milieux, quivalant l'inverse de la vitesse de transfert totale.
Ainsi, avec a taux de transfert total de gaz dans l'eau ($k_{tw}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), il est tabli que :
La relation de la r sistance au transfert entre l'oc an et l'atmosph re peut tre exprim e en termes des vitesses de transfert dans les deux milieux, correspondant l'inverse de la vitesse totale de transfert.
Ainsi, en utilisant a taux de transfert total de gaz dans l'air ($k_{ta}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), la relation suivante est tablie :
ID:(1633, 0)
