Druyd:Knowledge

Modelo SEIR

Storyboard

ID:(349, 0)

Modelos SEIR modificados

Definición

Modelos que incluyen los casos en que existen personas infectadas pero que aun no muestran síntomas y no contagian. Dichas personas se denominan personas latentes.

ID:(873, 0)

Curva del modelo SEIR

Imagen

En el caso de los modelos SEIR se tienen cuatro curvas, la de susceptibles, latentes, infectados y recuperados:

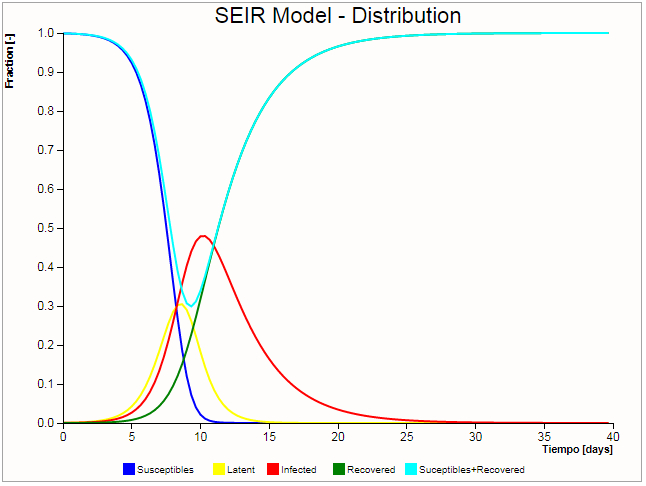
ID:(9703, 0)

Simulación del modelo SEIR

Nota

El modelo se puede resolver numéricamente las ecuaciones para los susceptibles S, infectados I, latentes E y recuperados R:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

en donde t es el tiempo \beta la taza de contagio, \sigma la taza de surgimiento de los síntomas en los infectados, \gamma la taza de recuperación, C el número de contactos, N la población, \mu_b la natalidad por habitante y \mu_d la mortalidad por habitante.

ID:(6834, 0)

Modelo SEIR

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$R_0$

R_0

Factor de Recuperación

$I_{crit}$

I_crit

Infectados Críticos

$I_t$

I_t

Infectados Totales al tiempo $t$

$E$

Latentes

$E_{crit}$

E_crit

Latentes Asimptótica

$C$

Número de Personas con que se Contacta

$N$

Población

$\beta$

beta

Probabilidad de Contagio por tiempo

1/s

$R_t$

R_t

Recuperados Totales al tiempo $t$

$S_{crit}$

S_crit

Susceptibles Críticos

$S_t$

S_t

Susceptibles Totales al tiempo $t$

$\mu_d$

mu_d

Tasa de Muerte por tiempo

$\mu_b$

mu_b

Tasa de Nacimiento por tiempo

$\sigma$

sigma

Tasa de Paso de Latente a Infectado por Tiempo

$\gamma$

gamma

Tasa de Recuperación por tiempo

1/s

$dI$

Variación de Infectados

$dE$

Variación de Latentes

$dR$

Variación de Recuperados

$dS$

Variación de Susceptibles

$dt$

Variación infinitesimal del tiempo

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

dS/dt=-(beta C/N)I(t)S(t)+mu_bN-mu_dS(t)

(ID 4086)

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

dE/dt=(beta C/N)I(t)S(t)-(sigma+mu_d)E(t)

(ID 4087)

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

dI/dt=sigma E(t)-(gamma+mu_d)I(t)

(ID 4088)

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

dR/dt=gamma I(t)-mu_dR(t)

(ID 4089)

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$

S_crit/N=(sigma+mu_d)(gamma+mu_d)/(beta C sigma)

(ID 4090)

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$

I_crit/N=(mu_bN-mu_dS_crit)/(beta C S_crit)

(ID 4091)

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$

E_crit/N=((gamma+mu_d)/sigma)I_crit/N

(ID 4092)

$R_0=\displaystyle\frac{\beta C\sigma}{(\sigma+\mu_d)(\gamma+\mu_d)}$

R_0=(beta C sigma)/((sigma+mu_d)(gamma+mu_d))

(ID 4093)

Ejemplos

Modelos SEIR modificados

Modelos que incluyen los casos en que existen personas infectadas pero que aun no muestran s ntomas y no contagian. Dichas personas se denominan personas latentes.

(ID 873)

Ecuaci n de susceptibles en el modelo SEIR

En el caso de los susceptibles el proceso de generar personas latentes en el modelo SEIR es equivalente a la de crear infectados en el modelo SIR. Por ello en este caso la ecuaci n que describe los susceptibles es igual en ambos modelos:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

(ID 4086)

Ecuaci n de latentes del modelo SEIR

En el caso de la ecuaci n de los casos latentes se tiene que primero considerar aquellos que se han contagiado y que el el modelo SIR conduc a a los infectados\\n\\n

$-\displaystyle\frac{\beta C}{N}I(t)S(t)$

\\n\\ndonde \beta es la probabilidad de infectados, C el n mero de contactos, S el numero de los susceptibles, I el numero de los infectados y N el numero de la poblaci n.\\n\\nEl numero de latentes descender en funci n de la fracci n \sigma que pase a mostrar los s ntomas y ser parte de los infectados con s ntomas I\\n\\n

$-\sigma E(t)$

\\n\\nDe igual forma se deben considerar aquellos que mueren por otra causa\\n\\n

$-\mu_d E(t)$

por lo que la ecuaci n para describir a los latentes ser

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

(ID 4087)

Ecuaci n de infectados en el modelo SEIR

En el caso de la ecuaci n de los casos infectado se tiene que primero considerar aquellos que son latentes E y que en la proporci n \sigma pasan a estar infectados

\sigma E(t)

El numero de infectados descender en funci n de la fracci n \gamma de los infectados I que se recupera

-\gamma I(t)

De igual forma se deben considerar aquellos que mueren por otra causa

-\mu_d I(t)

por lo que la ecuaci n para describir a los infectados ser

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

(ID 4088)

Ecuaci n de recuperados en el modelo SEIR

En el caso de la ecuaci n de los casos recuperados, se tiene que primero considerar aquellos que son infectados I y que en la proporci n \gamma pasan a estar recuperados\\n\\n

$\gamma I(t)$

\\n\\nDe igual forma se deben considerar aquellos que mueren por otra causa\\n\\n

$-\mu_d R(t)$

por lo que la ecuaci n para describir a los infectados ser

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

(ID 4089)

Factor de reproducci n en el modelo de SEIR

Si la probabilidad de infectarse es \beta, el n mero de contactos C, el factor de reproducci n \gamma, el factor de paso de latente a infectado y \mu_d el factor de muerte por otras causas, el factor de reproducci n es

$R_0=\displaystyle\frac{\beta C\sigma}{(\sigma+\mu_d)(\gamma+\mu_d)}$

(ID 4093)

N mero de susceptibles cr ticos, modelo SEIR

En el caso cr tico en que el sistema se vuelve estable el numero de latentes E no variara

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

y los infectados I

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

en donde S es el numero de susceptibles, \beta es la probabilidad de infectar, C numero de contactos, N numero de poblaci n, \gamma es el factor de recuperaci n, \mu_b el factor de nacimiento y \mu_d el de muerte.

El numero de latentes cr ticos se puede despejar de la segunda ecuaci n

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$

Si se reemplaza este valor en la primera ecuaci n se obtiene el valor cr ticos para los susceptibles

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$

que corresponde a la situaci n en que la curva de infectados alcanza su m ximo. Es decir el n mero de susceptibles cr ticos es el numero de susceptibles que van quedando al momento que el n mero de infectados alcanza su m ximo.

(ID 4090)

N mero de latentes cr ticos, modelo SEIR

De la ecuaci n de los infectados I

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

en que \gamma es el factor de recuperaci n, \sigma el factor de paso de latente a infectado, E los latentes y \mu_d el factor de los muertos.

Como el n mero de susceptibles en el caso cr ticos es

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$

se puede calcular el n mero cr tico de los infectados

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$

que corresponde a la situaci n en que la curva de infectados alcanza su m ximo. Es decir el n mero de latentes cr ticos es el numero de latentes que van quedando al momento que el n mero de infectados alcanza su m ximo.

(ID 4092)

N mero de infectados cr ticos, modelo SEIR

De la ecuaci n de los susceptibles S

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

en que \beta es la probabilidad de infecci n, C el n mero de contactos, N el n mero de la poblaci n, I los infectados, \mu_b el factor de los nacimientos y \mu_d el factor de los muertos.

Como el n mero de susceptibles en el caso asint tico es

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$

se puede calcular el n mero asintotico de los infectados

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$

(ID 4091)

Curva del modelo SEIR

En el caso de los modelos SEIR se tienen cuatro curvas, la de susceptibles, latentes, infectados y recuperados:

(ID 9703)

Simulaci n del modelo SEIR

El modelo se puede resolver num ricamente las ecuaciones para los susceptibles S, infectados I, latentes E y recuperados R:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

en donde t es el tiempo \beta la taza de contagio, \sigma la taza de surgimiento de los s ntomas en los infectados, \gamma la taza de recuperaci n, C el n mero de contactos, N la poblaci n, \mu_b la natalidad por habitante y \mu_d la mortalidad por habitante.

(ID 6834)

ID:(349, 0)