Usuario:


Modelo SIR
Storyboard

El modelo SIR considera una enfermedad que infecta personas susceptibles (S) formando infectados (I) que posteriormente se recuperan (R).

>Modelo

ID:(347, 0)


Simulación del modelo SIR
Html

El modelo se puede resolver numéricamente las ecuaciones para los susceptibles S, infectados I y recuperados R:

$\displaystyle\frac{dS}{dt}=-C\displaystyle\frac{I}{N}S\beta$



$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I$



$\displaystyle\frac{dR}{dt}=\gamma I$

en donde t es el tiempo \beta la taza de contagio, \gamma la taza de recuperación, C el número de contactos y N la población.

ID:(3022, 0)


Modelo SIR para describir SARS 2003 en Hong Kong
Imagen

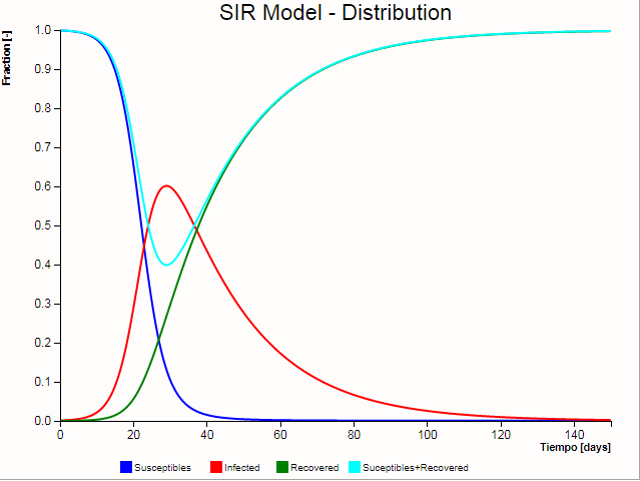
Si se observan los susceptibles, infectados y 'recuperados' (que se sanan o mueren) se observan las típicas curvas del modelo SIR:

ID:(9663, 0)