Utilizador:
Primeira Lei da Termodinâmica
Storyboard 
A primeira lei da termodinâmica estabelece que a energia é conservada e consiste em duas partes: uma associada ao trabalho e outra ao calor. Diferentemente do trabalho, esta última parte não pode ser completamente convertida em trabalho, o que limita as conversões energéticas possíveis.
ID:(1398, 0)
Mecanismos
Iframe
A primeira lei da termodinâmica, também conhecida como lei da conservação da energia, afirma que a energia não pode ser criada nem destruída em um sistema isolado; ela pode apenas ser transferida ou transformada. Esse princípio estabelece que a energia total de um sistema isolado permanece constante. Em termos práticos, isso significa que a mudança na energia interna de um sistema é igual ao calor adicionado ao sistema menos o trabalho realizado pelo sistema. A energia interna abrange a energia total dentro de um sistema, incluindo a energia cinética e potencial a nível molecular. O calor é a energia transferida entre sistemas devido a uma diferença de temperatura, enquanto o trabalho é a energia transferida quando uma força é aplicada sobre uma distância, frequentemente relacionada a mudanças de volume em gases. A primeira lei é fundamental para analisar a eficiência de motores térmicos, o desempenho de sistemas de refrigeração e aquecimento e para entender processos metabólicos em sistemas biológicos. Ela fornece uma base para compreender as transferências e transformações de energia em vários processos físicos, garantindo que a energia dentro de um sistema isolado seja sempre conservada.
Mecanismos
ID:(15250, 0)
Conservação de energia
Conceito
A primeira lei da termodinâmica estabelece que a energia é sempre conservada.
Enquanto na mecânica existe uma conservação similar, restrita a sistemas não dissipativos (por exemplo, excluindo o atrito), na termodinâmica essa lei é generalizada, considerando não apenas o trabalho mecânico, mas também o calor gerado ou absorvido pelo sistema.
Nesse sentido, a conservação de energia postulada na termodinâmica não possui restrições e é aplicável a todos os sistemas, desde que sejam consideradas todas as trocas e conversões de energia possíveis.
ID:(37, 0)
Primeira lei da termodinâmica
Conceito
A primeira lei da termodinâmica foi desenvolvida através de vários trabalhos [1,2], estabelecendo que a energia se conserva. Isso significa que o diferencial de energia interna ($dU$) é sempre igual a o diferencial de calor impreciso ($\delta Q$) fornecida ao sistema (positivo) menos o diferencial de trabalho impreciso ($\delta W$) realizada pelo sistema (negativo).
Portanto, temos:
| $ dU = \delta Q - \delta W $ |
Enquanto o diferencial exato não depende de como a variação é executada, o diferencial inexato depende. Quando nos referimos a um diferencial sem especificar que é inexato, assume-se que é exato.
[1] "Über die quantitative und qualitative Bestimmung der Kräfte" (Sobre a Determinação Quantitativa e Qualitativa das Forças), Julius Robert von Mayer, Annalen der Chemie und Pharmacie, 1842
[2] "Über die Erhaltung der Kraft" (Sobre a Conservação da Força), Hermann von Helmholtz, 1847
ID:(15700, 0)
Pressão e trabalho
Descrição
Consideremos um gás em um cilindro onde um pistão pode se deslocar. Se o pistão for movido, é possível reduzir o volume, comprimindo o gás. Para realizar essa compressão, é necessária uma energia que é igual à força exercida pelo gás multiplicada pela distância percorrida pelo pistão. Essa energia também pode ser representada em função da pressão, já que a pressão é definida pela força e pela área do pistão.
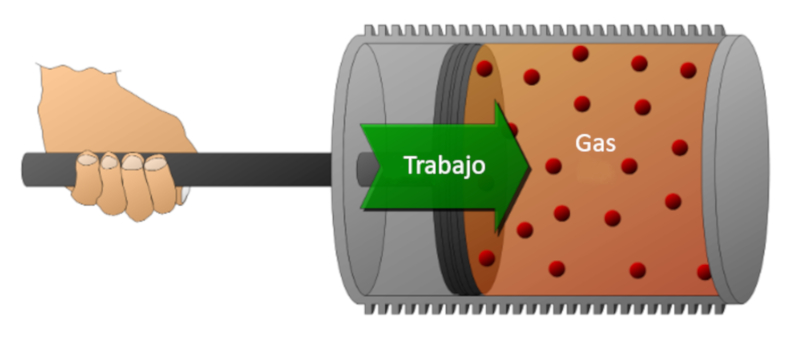
O trabalho pode ser realizado pelo sistema (compressão) ou pelo sistema sobre o meio externo (expansão).
Uma vez que la força mecânica ($F$) dividido por la seção ($S$) é igual a la pressão ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
e la variação de volume ($dV$) com o distância percorrida ($dx$) é igual a:
| $ \Delta V = S \Delta s $ |
A equação para o diferencial de trabalho impreciso ($\delta W$) pode ser expressa como:
| $ \delta W = F dx $ |
Portanto, ela pode ser escrita como:
| $ \delta W = p dV $ |
ID:(11126, 0)
Primeira lei da termodinâmica e pressão
Conceito
Uma vez que o diferencial de energia interna ($dU$) está relacionado com o diferencial de calor impreciso ($\delta Q$) e o diferencial de trabalho impreciso ($\delta W$) da seguinte forma:
| $ dU = \delta Q - \delta W $ |
E é sabido que o diferencial de trabalho impreciso ($\delta W$) está relacionado com la pressão ($p$) e la variação de volume ($dV$) como segue:
| $ \delta W = p dV $ |
Portanto, podemos concluir que:
| $ dU = \delta Q - p dV $ |
ID:(15701, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ dU = \delta Q - \delta W $
dU = dQ - dW
$ dU = \delta Q - p dV $
dU = dQ - p * dV
$ dV = S dx $
DV = S * Ds
$ \delta W = F dx $
dW = F * dx
$ \delta W = p dV $
dW = p * dV
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
ID:(15309, 0)
Primeira lei da termodinâmica
Equação
O diferencial de energia interna ($dU$) é sempre igual à quantidade de o diferencial de calor impreciso ($\delta Q$) fornecida ao sistema (positiva) menos a quantidade de o diferencial de trabalho impreciso ($\delta W$) realizada pelo sistema (negativa):
| $ dU = \delta Q - \delta W $ |
ID:(9632, 0)
Trabalho
Equação
A relação entre o trabalho e as nossas ações está ligada à dependência de o diferencial de trabalho impreciso ($\delta W$) em relação à distância percorrida. Se considerarmos uma força mecânica ($F$) para mover um objeto ao longo de um distância percorrida ($dx$), a energia necessária pode ser expressa da seguinte forma:
| $ \delta W = F dx $ |
A notação $\delta W$ é usada para indicar a variação do trabalho, ao contrário de $dW$, que nos lembra que o seu valor depende do processo de variação do comprimento $dx$. Um exemplo disso ocorreria se o deslocamento ocorresse em um gás e uma mudança nele ocorresse, nesse caso:
$\delta W < Fdx$
ID:(3202, 0)
Definição de pressão
Equação
La pressão da coluna de água ($p$) é calculado a partir de la força da coluna ($F$) e la altura da coluna líquida ($S$) da seguinte forma:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Elemento de volume
Equação
Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma distância de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), então é igual a:
| $ dV = S dx $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 0)
Pressão e trabalho
Equação
O diferencial de trabalho impreciso ($\delta W$) é igual a la pressão ($p$) multiplicado por la variação de volume ($dV$):
| $ \delta W = p dV $ |
Uma vez que la força mecânica ($F$) dividido por la seção ($S$) é igual a la pressão ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
e la variação de volume ($dV$) com o distância percorrida ($dx$) é igual a:
| $ \Delta V = S \Delta s $ |
A equação para o diferencial de trabalho impreciso ($\delta W$) pode ser expressa como:
| $ \delta W = F dx $ |
Portanto, ela pode ser escrita como:
| $ \delta W = p dV $ |
ID:(3468, 0)
Primeira lei da termodinâmica e pressão
Equação
Com a primeira lei da termodinâmica, pode ser expressa em termos de o diferencial de energia interna ($dU$), o diferencial de calor impreciso ($\delta Q$), la pressão ($p$) e la variação de volume ($dV$) como:
| $ dU = \delta Q - p dV $ |
Uma vez que o diferencial de energia interna ($dU$) está relacionado com o diferencial de calor impreciso ($\delta Q$) e o diferencial de trabalho impreciso ($\delta W$) da seguinte forma:
| $ dU = \delta Q - \delta W $ |
E é sabido que o diferencial de trabalho impreciso ($\delta W$) está relacionado com la pressão ($p$) e la variação de volume ($dV$) como segue:
| $ \delta W = p dV $ |
Portanto, podemos concluir que:
| $ dU = \delta Q - p dV $ |
ID:(3470, 0)