User:
Avogadro Principle
Storyboard 
Avogadro's principle states that the division of the number of moles ($n$) by the volume ($V$) is constant while the pressure ($p$) and the absolute temperature ($T$) are constant.
This means that the number of moles ($n$) varies proportionally with the volume ($V$).
ID:(1475, 0)
Mechanisms
Iframe
Avogadro's principle states that equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules. This means that the volume of a gas is directly proportional to the number of molecules (or moles) present when temperature and pressure are held constant. The principle is fundamental in understanding the behavior of gases and forms the basis for the ideal gas law. It allows for the determination of the amount of gas in a given volume and is essential for calculations involving chemical reactions and gas mixtures.
Mechanisms
ID:(15257, 0)
Variation of volume and number of moles
Concept
There are intensive and extensive variables. The former are characteristics of the system's state and do not depend on its size. Two examples are the pressure ($p$) and the absolute temperature ($T$). If we desire a larger system in the same state, both the pressure ($p$) and the absolute temperature ($T$) must remain unchanged.
The situation is different with the volume ($V$), which is an extensive variable, meaning that if a larger system is needed, this variable will have to increase in the corresponding proportion. The same goes for the total number of moles ($n$):
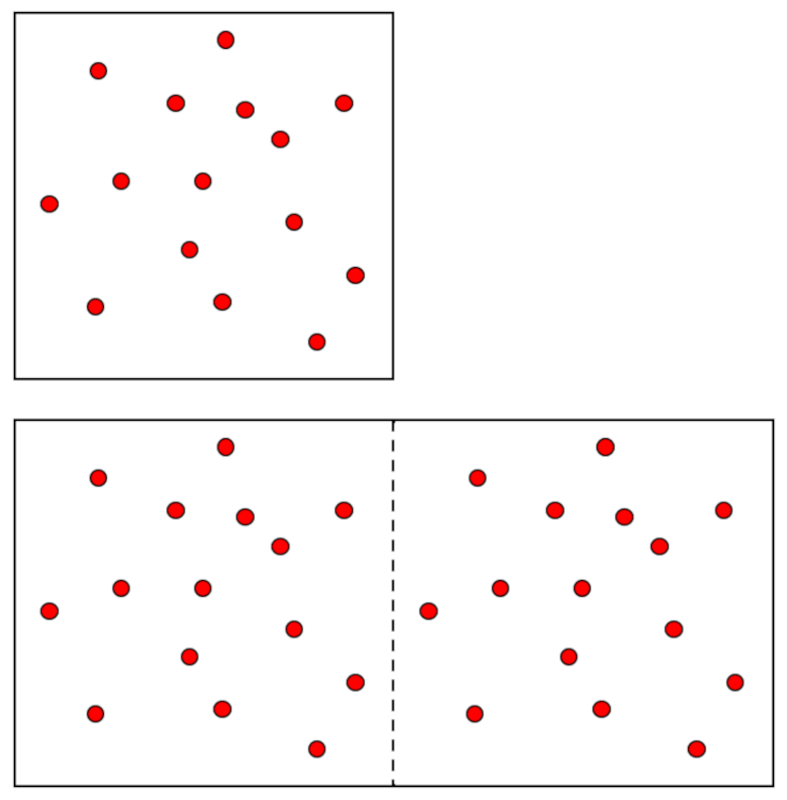
Furthermore, both variables must increase in the same proportion, so if the pressure ($p$) and the absolute temperature ($T$) are constant, they will be proportional to each other:
$n \propto V$
ID:(15696, 0)
Moles and volume ratio
Description
In a gas, when the pressure ($p$) and the absolute temperature ($T$) are held constant, a proportional relationship is observed between the volume ($V$) and the number of moles ($n$). Each time the volume ($V$) increases, it is observed that the number of moles ($n$) also increases, and vice versa,
$n \propto V$
as shown in the following graph:
Avogadro's Law [1] states that the volume ($V$) and the number of moles ($n$) are directly proportional when the pressure ($p$) and the absolute temperature ($T$) are held constant.
This relationship can be expressed as follows, using the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
[1] "Essay on a Method of Determining the Relative Masses of the Elementary Molecules of Bodies and the Proportions in Which They Enter into These Compounds," Amedeo Avogadro, Journal de Physique, 73, 58-76 (1811).
ID:(9532, 0)
Amedeo Avogadro
Description
Amadeo Avogadro, full name Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto, was an Italian scientist born on August 9, 1776, and died on July 9, 1856. Avogadro is best known for his contributions to the development of molecular theory and the formulation of Avogadro's law. He proposed that equal volumes of gases, at the same temperature and pressure, contain an equal number of particles, which is now known as Avogadro's principle or Avogadro's law. This concept was instrumental in the development of the concept of the mole and provided a foundation for understanding the relationships between the amount of substance, volume, and number of particles in gases. Despite his significant contributions, Avogadro's work was not widely recognized during his lifetime, and his ideas gained greater acceptance years after his death. Today, Avogadro is honored for his fundamental contributions to chemistry and is considered one of the pioneers of modern molecular theory.
ID:(1659, 0)
Change of state of an ideal gas according to Avogadro's Law
Concept
Avogadro's principle states that when the pressure ($p$) and the absolute temperature ($T$) are held constant, the ratio of número de Moles ($n$) to the volume ($V$) equals the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
This means that if a gas transitions from an initial state (the number of moles in state i ($n_i$) and the volume in state i ($V_i$)) to a final state (the number of moles in state f ($n_f$) and the volume in state f ($V_f$)) while maintaining the pressure ($p$) and the absolute temperature ($T$) constant, Gay-Lussac's law must always hold:
$\displaystyle\frac{n_i}{V_i}=C_a=\displaystyle\frac{n_f}{V_f}$
Therefore, we have:
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
ID:(15695, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$\displaystyle\frac{ n_i }{ V_i } = C_a $
n / V = C_a
$\displaystyle\frac{ n_f }{ V_f } = C_a $
n / V = C_a
$\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$
n_i / V_i = n_f / V_f
ID:(15316, 0)
Avogadro's Law (1)
Equation
Avogadro's Law states that the volume ($V$) and the number of moles ($n$) are directly proportional when the pressure ($p$) and the absolute temperature ($T$) are held constant.
This relationship can be expressed as follows, using the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n_i }{ V_i } = C_a $ |
| $\displaystyle\frac{ n }{ V } = C_a $ |
ID:(580, 1)
Avogadro's Law (2)
Equation
Avogadro's Law states that the volume ($V$) and the number of moles ($n$) are directly proportional when the pressure ($p$) and the absolute temperature ($T$) are held constant.
This relationship can be expressed as follows, using the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n_f }{ V_f } = C_a $ |
| $\displaystyle\frac{ n }{ V } = C_a $ |
ID:(580, 2)
Change of state of an ideal gas according to Avogadro's Law
Equation
If a gas transitions from an initial state (i) to a final state (f) while keeping the pressure ($p$) and the absolute temperature ($T$) constant, then for the number of moles in state i ($n_i$), the volume in state i ($V_i$), the number of moles in state f ($n_f$), and the volume in state f ($V_f$), it holds true:
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
Avogadro's principle states that when the pressure ($p$) and the absolute temperature ($T$) are held constant, the ratio of número de Moles ($n$) to the volume ($V$) equals the constant of Avogadro's principle ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
This means that if a gas transitions from an initial state (the number of moles in state i ($n_i$) and the volume in state i ($V_i$)) to a final state (the number of moles in state f ($n_f$) and the volume in state f ($V_f$)) while maintaining the pressure ($p$) and the absolute temperature ($T$) constant, Gay-Lussac's law must always hold:
$\displaystyle\frac{n_i}{V_i}=C_a=\displaystyle\frac{n_f}{V_f}$
Therefore, we have:
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
ID:(3489, 0)