Training Gas Laws
Storyboard 
In a device in which pressure, volume and temperature can be modified, different initial states are defined and explores how this varies by changing two of the state variables each time.
ID:(1317, 0)
Boyle's Law Experiment
Description 
To study Boyle's Law, the following elements are required:
• Manual air pump
• Gas volume-controlled thermometer
The gas volume-controlled thermometer is a tube that contains another tube connected to the pump and holds a small volume of mercury.
The external cylinder allows the temperature for the experiment to be set.
As the pressure is increased with the pump, the mercury moves, compressing the enclosed volume. This allows for the measurement of the associated volume for each pressure, ensuring that the temperature remains constant.
Additionally, the mercury encapsulates the volume, ensuring that the number of moles remains constant.
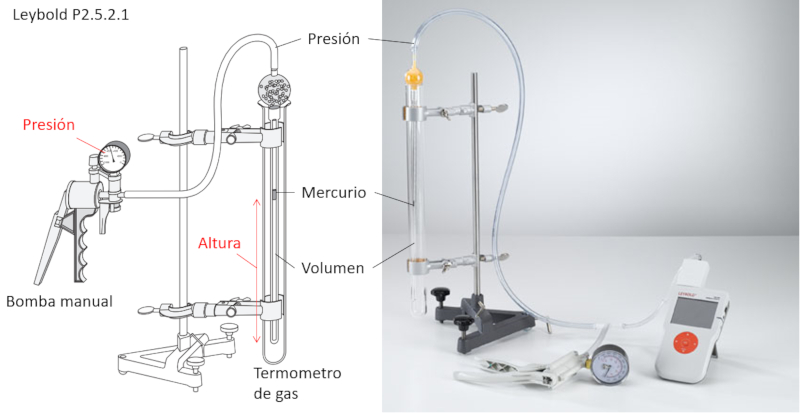
ID:(11174, 0)
Boyle's Law Experiment, Data
Description 
If the experiment is conducted with a defined temperature and number of gas moles, data can be observed as listed and represented in the following graph:
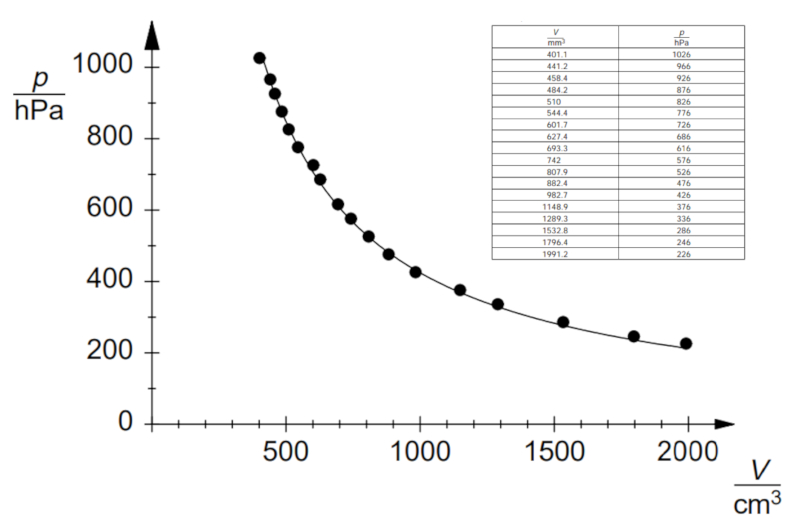
This demonstrates Boyle's Law, which states that the pressure $p$ and volume $V$ vary inversely according to the following relationship:
| $ p V = C_b $ |
ID:(11177, 0)
Charles's Law Experiment
Description 
To study Charles' Law, the following equipment is required:
• A gas thermometer with controlled volume
• A temperature measurement probe
In this case, the inner cylinder of the gas thermometer can be left open if using ambient pressure, or it can be sealed with a pump to maintain a defined pressure.
To perform the measurement, the temperature is varied in the outer cylinder of the gas thermometer, and the temperature value is measured with the probe.
Additionally, the movement of the mercury volume is observed as it increases or decreases, which can be measured.
Moreover, the mercury encapsulates the volume, ensuring that the number of moles remains constant.

ID:(11175, 0)
Charles's Law Experiment, Data
Description 
If the experiment is conducted with a defined pressure and number of gas moles, data can be obtained as listed and represented in the following graph:
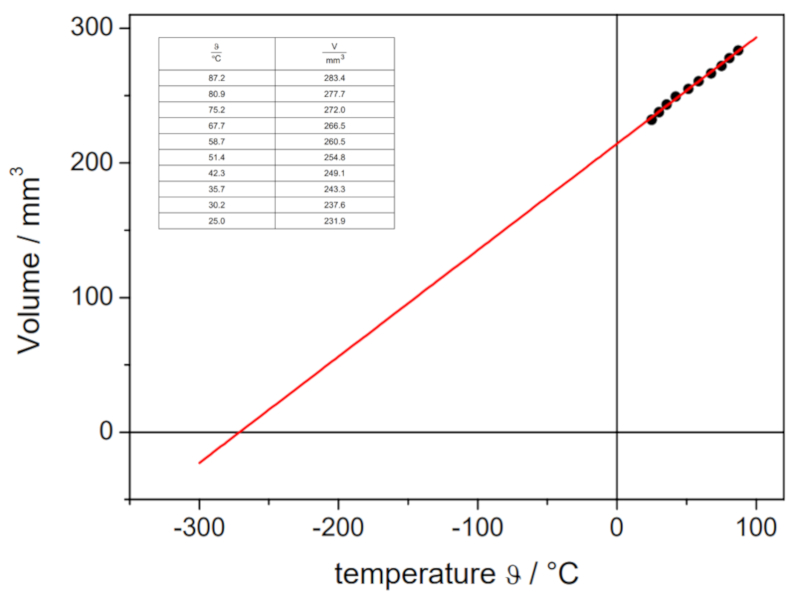
This illustrates Charles' Law, which states that the temperature $T$ and the volume $V$ vary proportionally according to the following relationship:
| $\displaystyle\frac{ V }{ T } = C_c$ |
ID:(11178, 0)
Gay Lussac's Law Experiment
Description 
To study Gay-Lussac's law, the following equipment is needed:
• Manual air pump
• Gas thermometer with controlled volume
• Temperature measurement probe
In this case, you work with a predefined volume.
To perform the measurement, the temperature is varied in the outer cylinder of the gas thermometer, and the temperature value is measured with the probe.
Then, the pressure is adjusted using a pump until the volume reaches the predefined value.
The experiment is repeated with another temperature, readjusting the pressure to achieve the same volume.
Additionally, the mercury encapsulates the volume, ensuring that the number of moles remains constant.

ID:(11176, 0)
Gay Lussac's Law Experiment, Data
Description 
If the experiment is conducted with a defined volume and number of gas moles, data can be obtained as listed and represented in the following graph:
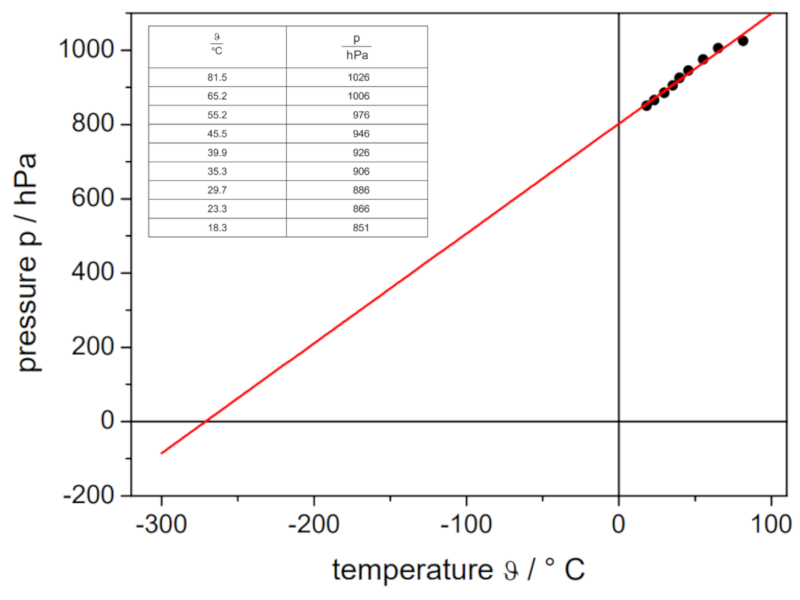
This illustrates Gay-Lussac's law, which states that the temperature $T$ and the pressure $p$ vary proportionally according to the following relationship:
| $\displaystyle\frac{ p }{ T } = C_g$ |
ID:(11180, 0)
Hand pump
Description 
To pump gas, an instrument is constructed that consists of a chamber and a piston with two openings.
Each time the piston is retracted (suction), the gas enters the compression chamber through the open inlet while the outlet remains closed.
Then, when the piston is moved to generate pressure, it displaces with the opening closed, compressing the gas until its pressure exceeds that of the system where the gas is to be injected. At that moment, the second opening opens, allowing the compressed gas to escape and contribute to further increasing the pressure of the system being compressed.
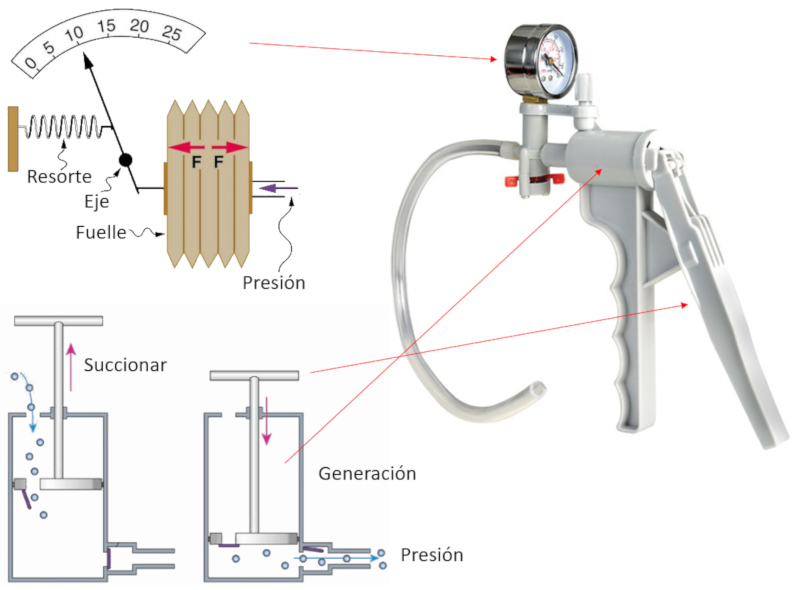
The achieved pressure is mechanically measured using a membrane connected to a needle that moves according to the displacement, indicating the achieved pressure.
ID:(11181, 0)
Gas thermometer
Description 
The gas-filled piston is immersed in the liquid being measured, causing the gas to expand or contract with temperature changes. The gas pressure is balanced with the mercury column, and the height can be calibrated according to temperature:
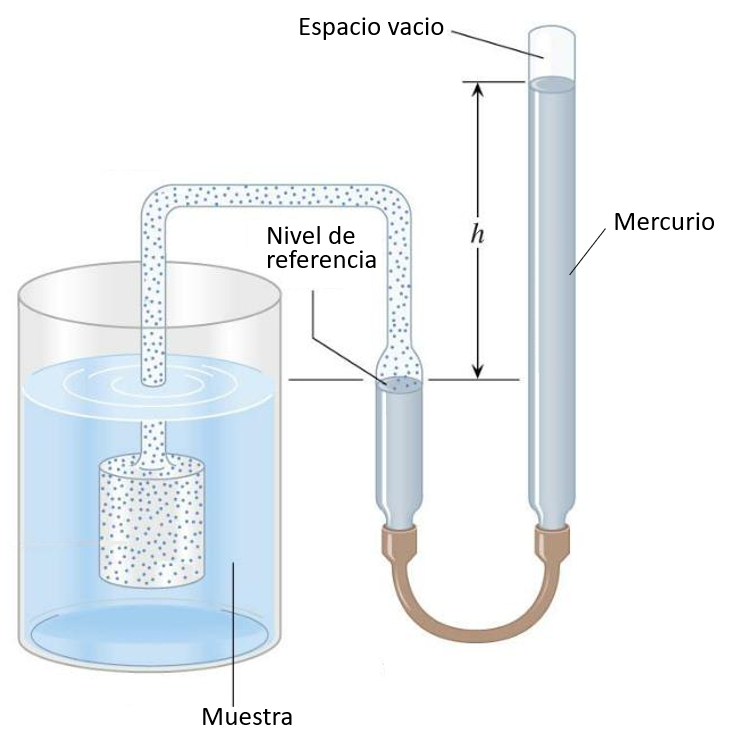
In gas experiments, a vacuum cavity is used to enclose the gas for the desired experiment. Instead of using a gas to measure temperature, it is employed to apply the desired pressure.
ID:(11179, 0)
