User:


Poisson distributions
Storyboard

In the case where the probability is very small, the binomial distribution is reduced to a Poisson distribution.

>Model

ID:(1555, 0)


Example comparison with Poisson distribution
Description

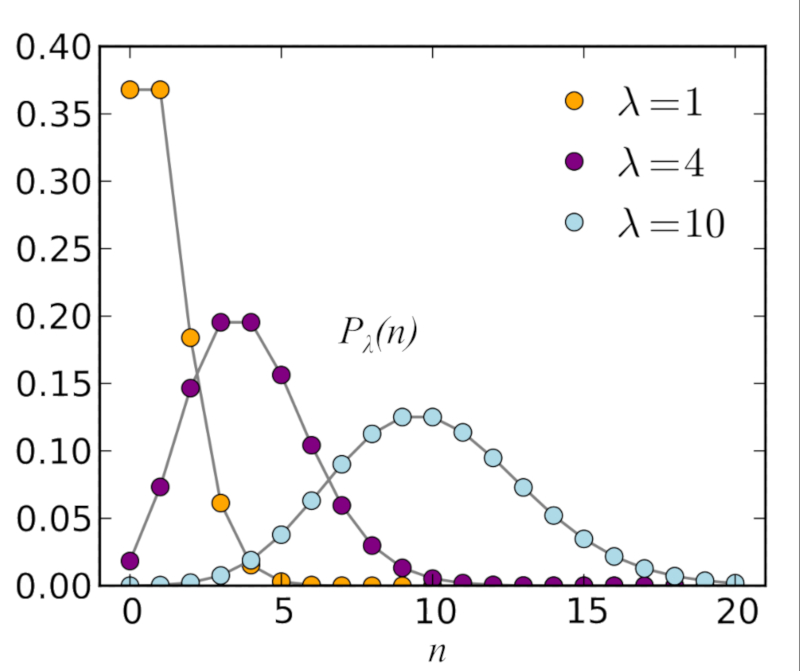
If we study the binomial distribution for large numbers N and very small probability p \ ll 1 it can be approximated using a Poisson distribution. The comparison can be done with the following simulator:

ID:(7794, 0)


Poisson distributions
Description

In the case where the probability is very small, the binomial distribution is reduced to a Poisson distribution.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$e^{-\lambda}$
elam
Exponential $e^{-\lambda}$
-
$N^n$
N^n
Exponential $N^n$
-
$n!$
n!
Factorial $n!$
-
$n$
n
Number
-
$N$
N
Número total de pasos
-
$n$
n
Número totales de pasos a la izquierda
-
$\lambda^n$
lambda_n
Power of lambda $\lambda^n$
-
$P_N(m)$
P_Nm
Probabilidad de $n_1$ de $N$ pasos hacia la izquierda
-
$p$
p
Probabilidad de pasos hacia la izquierda
-
$\lambda$
lam
Standard Deviation Poisson
-

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

Con la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$



con el n mero total de pasos es

$N=n_1+n_2$



y solo existe la probabilidad de ir a la derecha o a la izquierda, con se tiene para las probabilidades que

$p+q=1$



por lo que con se tiene la distribuci n binomial

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

(ID 8961)

Therefore expressions such as N!/(Nn)! for N large (N\gg 1) and n small (N\gg n) can be approximated with

$u!\sim\sqrt{2\pi u}\left(\displaystyle\frac{u}{e}\right)^u$



with what you get with N\gg n

\displaystyle\frac{N!}{(N-n)!}\sim\displaystyle\frac{\sqrt{2\pi N}}{\sqrt{2\pi (N-n)}}\displaystyle\frac{N^N}{(N-n)^{N-n}}\displaystyle\frac{e^{N-n}}{e^N}\sim N^n

that is

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$

(ID 4738)

With the approximation

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$



and employing

$\lambda=Np$



it can be shown that

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$

(ID 8969)

How the exponential is defined as

$e^z\sim\left(1+\displaystyle\frac{z}{u}\right)^u$



and by entering

$\lambda=Np$



you can replace z=-\lambda=-Np and u=N-n with N\gg n what results

$e^{-\lambda}\sim (1-p)^{N-n}$

(ID 8968)

Since the probability of taking n steps in one direction is

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$



for a large number N and the probability is very small p \ll 1 can be approximated

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$



and

$e^{-\lambda}\sim (1-p)^{N-n}$



the binomial distribution is reduced to a Poisson distribution:

$ P_{\lambda}(n) =\displaystyle\frac{ \lambda ^ n }{ n! }e^{- \lambda }$

(ID 3369)

If we study the binomial distribution for large numbers N and very small probability p \ ll 1 it can be approximated using a Poisson distribution. The comparison can be done with the following simulator:

(ID 7794)

ID:(1555, 0)