El método de la Mecánica Estadística
Storyboard 
Cada área de la física se caracteriza por un concepto clave y una o más ecuaciones asociadas. En la mecánica, se trata de describir el movimiento, y las ecuaciones clave son las leyes de Newton. En electromagnetismo, se enfoca en comprender la interacción de las cargas eléctricas, donde la ecuación principal es la ley de Coulomb, que establece que la fuerza disminuye cuadráticamente con la distancia. De manera similar, en la mecánica cuántica, encontramos la ecuación de Schrödinger y el concepto de función de onda.
En la mecánica estadística, el desafío es modelar sistemas compuestos por múltiples partículas, lo que a primera vista podría parecer imposible de resolver. Sin embargo, con una idea bastante simple, el problema se reduce a contar estados basados en parámetros microscópicos y calcular las probabilidades asociadas con los estados macroscópicos. Los estados microscópicos se describen en función del espacio de fase propio de la mecánica, y se cuantifican para determinar la distribución de probabilidades y, de esta manera, analizar estadísticamente la probabilidad de que el sistema exhiba un comportamiento específico.
ID:(307, 0)
¿Qué es Mecánica Estadística?
Descripción 
En mecánica aprendemos que podemos modelar como cuerpos se comportan. Sin embargo si consideramos un sistema como un gas tendremos
Una posibilidad seria no trabajar con soluciones individuales si no que con distribuciones de estas. O sea no calcular el comportamiento de cada partícula si no que desarrollar una teoría que, basado en conceptos de la mecánica o mecánica cuántica, nos permite calcular la distribución que nos indica como se distribuyen las soluciones.
La pregunta es ahora ¿como podemos calcular dichas distribuciones?
ID:(502, 0)
Video 'What is NOT Random'
Descripción 
Video 'What is NOT Random' de Derek Muller
No es sobre Mecánica Estadística pero ayuda a entender muchos conceptos relacionados que se discuten (con imágenes del video) en las próximas laminas.
ID:(13040, 0)
El demonio de Laplace
Imagen 
Laplace introduce el concepto de un observador (posteriormente caricaturizado como el demonio de Laplace) que observa todas las posiciones de todas las partículas en un sistema y todas las interacciones que existen y puede con ello:
- pronosticar la evolución futura
- determinar la historia pasada

Con ello el mundo se vuelve deterministico. No existe el azar. Tampoco existiría el libre albedrío:
- toda decisión que aparentemente tomamos es la consecuencia determinista de la situación en que nos encontrábamos
- en ese sentido no seriamos responsables de nuestros actos ya que no existe la posibilidad de que podamos elegir libremente
ID:(13041, 0)
¿Qué es la física?
Imagen 
La física es por ello las reglas que me permiten calcular el nuevo estado a partir de un estado anterior.
Como analogía, si uno considera un video este se puede descomponer en múltiples pixeles. De un cuadro al otro solo algunos pixeles cambian.

Las reglas de comportamiento por ello indican
- cuales pixeles cambian
- de que forma cambian
ID:(13042, 0)
¿Se conserva la información?
Imagen 
La pregunta clave es si un sistema en un estado simple (poca información) evoluciona de modo de que la información se conserva. Esto es, por complejo que parezca, no incrementa la cantidad de información que contiene.

Como las ecuaciones de movimiento son invariantes ante una inversión del tiempo, esto significaría que el sistema puede volver a su estado inicial en forma espontanea. Parecería que se 'ordena' pues nunca realmente se 'desordeno'.
Sin embargo sabemos que esto no es asi:
Los sistemas no vuelven en forma espontanea a su estado inicial 'ordenado' por lo que existe un 'desordenamiento' natural.
El desordenamiento significa que se requiere mas información para describir el sistema. Por ello
La información no se conserva en el tiempo y tiende a aumentar.
La cantidad de información de un sistema se denomina la entropía de este.
ID:(13043, 0)
Consecuencia del aumento de información
Imagen 
El aumento de la información lleva a que:
- existen mas de un nuevo estado que el sistema puede asumir, no existiendo la posibilidad de pronosticar cual estado el sistema asume
- puede ser posible de determinar el sistema que origina el estado final
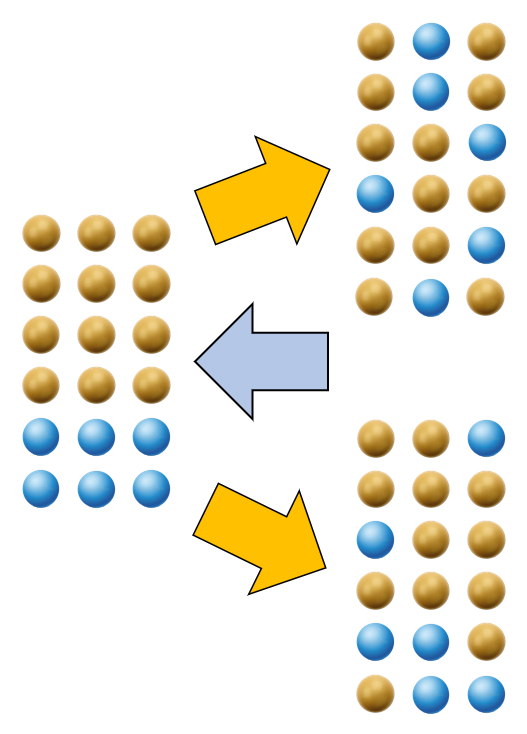
Esto lleva a que
- solo se puede dar una probabilidad de un nuevo estado que el sistema va a asumir
- en forma análoga la vuelta al sistema original se asocia a una probabilidad y esta puede ser infinitesimal
ID:(13046, 0)
¿Cómo se crea información?
Imagen 
Mucho antes de que se descubriera la mecánica cuántica dentro de la termodinámica surgió la llamada paradoja de Gibbs. Esta surja cuando uno intenta sumar la entropía de dos sistemas individuales y la compara con aquella de un sistema del tamaño de ambos combinados.
La solución de la paradoja lleva a que se determinara que las partículas de las que esta conformado el sistema tienen que ser indistinguibles. Esto lleva a que cuando interactuan no es posible saber cual que ellas corresponde a cual implicando que se crean nuevas alternativas:
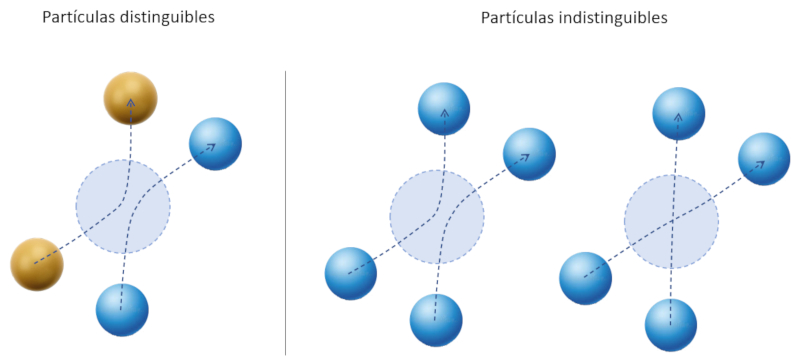
Las nuevas alternativas corresponden a información adicional que se debe tener para definir los posibles estados.
Nota: en el video de Derek Muller de Veritasium se explora el efecto mecánico cuántico sin hacer alusión a la paradoja de Gibbs.
ID:(13044, 0)
Forma de trabajar de la Mecánica Estadística
Imagen 
La mecánica estadística no busca resolver las ecuaciones de movimiento del sistema. Busca reconocer como las ecuaciones de movimiento acotan los estados posibles reconociendo patrones generales que permiten describir el estado del sistema y su evolución.
En la analogía de una imagen, la situación de máxima información (entropía) y a su vez de perfecto caos es un cuadro de pixeles elegidos al azar.

Un sistema real presenta una estructura, un orden, que en la analogía del cuadro correspondería a una imagen en que se reconocen estructuras como son la agrupación de colores. Variaciones dentro dichos pixeles no se re-conocerán siendo para el observador un cuadro equivalente. Lo análogo ocurre en un sistema físico en que existen múltiples variaciones sobre las condiciones que describen el mismo macro estado del sistema. En ese sentido
la mecánica estadística estudia ensambles (conjuntos) de estados posibles en función de parámetros macroscopicos que los acotan y determina su probabilidad de que existan.
ID:(13045, 0)
Microscopicamente distinto, macroscopicamente similar
Descripción 
Las múltiples alternativas que significan
Sin embargo muchos de esos estados microscópicos son muy similares si no idénticos en un nivel macroscópico.
Si al final solo existe un numero discreto de estados macroscópicos posibles se puede estimar su probabilidad de existencia en función del numero de estados microscópicos que se asocian a estos.
De esta forma la mecánica estadística resuelve el problema
• determinando los estados microscópicos posibles
• determinando los estados macroscópicos que se asocian a los microscópicos
• determinando mediante el numero de estados microscópicos la probabilidad de cada estado macroscópico
ID:(11400, 0)
Necesidad de mecánica
Descripción 
Al buscar describir el estado del sistema de
Para ello:
se consideran los estados posibles en el sistema de fase
se estudian las restricciones que existen sobre los estados posibles (ejemplo energía total dada)
se buscan métodos para poder contabilizar el numero de estados que existen bajo las restricciones dadas
ID:(11401, 0)
Necesidad de estadística
Descripción 
Al obtener los estados macroscópicos posibles y la frecuencia es necesario desarrollar un trabajo de análisis estadístico:.
• establecer la distribución de la probabilidad de que se de cada estado macroscópico
• estudiar como la distribución evoluciona en función de los parámetros macroscópicos del sistema
• en la mayoría de los casos el resultado es que existe un estado macroscópico de alta probabilidad y
• la distribución entrega información sobre la dispersión que pueden tener los distintos parámetros
ID:(11402, 0)
0
Video
Video: ¿Qué es Mecánica Estadística?
