Storyboard

Jeder Bereich der Physik wird durch ein Schlüsselkonzept und eine oder mehrere zugehörige Gleichungen charakterisiert. In der Mechanik geht es darum, Bewegungen zu beschreiben, wobei die Gesetze von Newton die Schlüsselgleichungen darstellen. In der Elektromagnetismus steht die Wechselwirkung von elektrischen Ladungen im Fokus, wobei die Hauptgleichung das Coulombsche Gesetz ist, das besagt, dass die Kraft quadratisch mit dem Abstand abnimmt. In der Quantenmechanik finden wir die Schrödinger-Gleichung und das Konzept der Wellenfunktion.

In der statistischen Mechanik besteht die Herausforderung darin, Systeme zu modellieren, die aus mehreren Teilchen bestehen, was auf den ersten Blick unmöglich zu lösen erscheint. Mit einer recht einfachen Idee reduziert sich das Problem jedoch darauf, Zustände auf der Grundlage mikroskopischer Parameter zu zählen und die mit makroskopischen Zuständen verbundenen Wahrscheinlichkeiten zu berechnen. Mikroskopische Zustände werden mithilfe des für die Mechanik typischen Phasenraums beschrieben und quantifiziert, um die Wahrscheinlichkeitsverteilung zu bestimmen und somit die Wahrscheinlichkeit zu analysieren, dass das System ein bestimmtes Verhalten zeigt.

>Modell

ID:(307, 0)

Beschreibung

>Top

In der Mechanik lernen wir, dass wir modellieren können, wie sich Körper verhalten. Wenn wir jedoch ein System als Gas betrachten, werden wir 10^{23} Partikel haben, wird die Anwendung der Konzepte der Mechanik kompliziert. Einerseits gibt es die hohe Komplexität der Lösung eines Systems von 10^{23} -Gleichungen, andererseits würden wir nicht wissen, was wir mit diesem Ergebnis tun sollen. Deshalb müssen wir einen anderen Ansatz suchen.

Eine Möglichkeit wäre, nicht mit individuellen Lösungen zu arbeiten, sondern mit deren Verteilungen. Das heißt, nicht das Verhalten jedes Teilchens zu berechnen, sondern eine Theorie zu entwickeln, die es uns ermöglicht, basierend auf Konzepten der Quantenmechanik oder -mechanik die Verteilung zu berechnen, die uns sagt, wie die Lösungen verteilt sind.

Die Frage ist nun, wie wir diese Verteilungen berechnen können.

ID:(502, 0)

Beschreibung

>Top

Video 'What is NOT Random' von Derek Muller

Es geht nicht um Statistische Mechanik, aber es hilft, viele verwandte Konzepte zu verstehen, die (mit Bildern aus dem Video) in den nächsten Folien diskutiert werden.

ID:(13040, 0)

Bild

>Top

Laplace führt das Konzept eines Beobachters ein (später als Laplace-Dämon karikiert), der alle Positionen aller Teilchen in einem System und alle Wechselwirkungen beobachtet, die existieren und mit ihm möglich sind:
- zukünftige Entwicklungen prognostizieren
- Vergangenheit bestimmen

Damit wird die Welt deterministisch. Es gibt keine Chance. Es würde auch keinen freien Willen geben:

- Jede Entscheidung, die wir anscheinend treffen, ist die deterministische Folge der Situation, in der wir uns befanden

- In diesem Sinne wären wir nicht für unser Handeln verantwortlich, da es keine Möglichkeit gibt, dass wir frei wählen können

ID:(13041, 0)

Bild

>Top

Physik ist daher die Regel, nach der ich den neuen Zustand aus einem früheren Zustand berechnen kann.
Wenn man ein Video betrachtet, kann es analog in mehrere Pixel zerlegt werden. Von einem Bild zum anderen ändern sich nur wenige Pixel.

Die Verhaltensregeln geben daher an

- Welche Pixel ändern sich

- Wie verändern sie sich

ID:(13042, 0)

Bild

>Top

Die Schlüsselfrage ist, ob sich ein System in einem einfachen Zustand (wenig Information) so entwickelt, dass die Information erhalten bleibt. Dies ist, so komplex es auch scheinen mag, es erhöht nicht die Menge an Informationen, die es enthält.

Da die Bewegungsgleichungen unter Zeitumkehr unveränderlich sind, würde dies bedeuten, dass das System spontan in seinen Ausgangszustand zurückkehren kann. Es scheint, dass es 'geordnet' ist, weil es nie wirklich 'ungeordnet' war.

Wir wissen jedoch, dass dies nicht der Fall ist:

Systeme kehren nicht spontan in ihren ursprünglichen 'geordneten' Zustand zurück, daher liegt eine natürliche 'Unordnung' vor.

Unordnung bedeutet, dass mehr Informationen erforderlich sind, um das System zu beschreiben. So

Informationen bleiben im Laufe der Zeit nicht erhalten und nehmen tendenziell zu.

Die Informationsmenge in einem System wird als Entropie bezeichnet.

ID:(13043, 0)

Bild

>Top

Die Zunahme der Informationen führt zu:
- Es gibt mehr als einen neuen Zustand, den das System annehmen kann, ohne dass die Möglichkeit besteht, vorherzusagen, welchen Zustand das System annimmt
- Es kann möglich sein, das System zu bestimmen, aus dem der Endzustand stammt

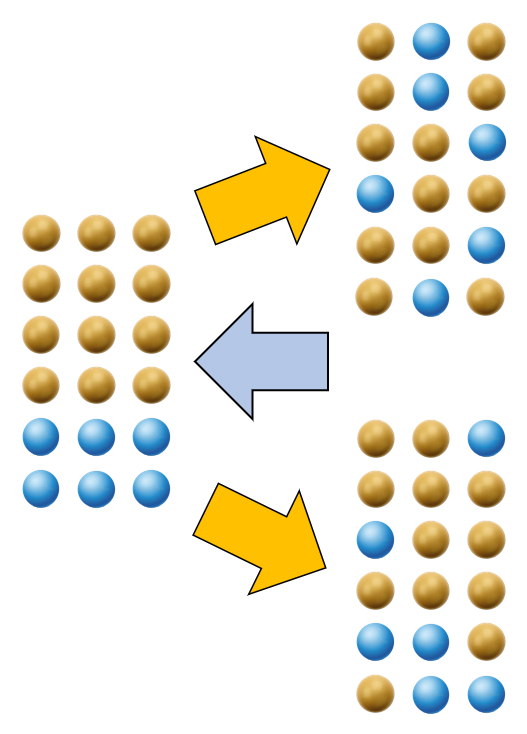
Dies führt zu

- Sie können nur die Wahrscheinlichkeit eines neuen Zustands angeben, den das System annehmen wird

- In analoger Weise ist die Rückkehr zum ursprünglichen System mit einer Wahrscheinlichkeit verbunden, die infinitesimal sein kann

ID:(13046, 0)

Bild

>Top

Lange bevor die Quantenmechanik in der Thermodynamik entdeckt wurde, entstand das sogenannte Gibbs-Paradoxon. Dies entsteht, wenn man versucht, die Entropie zweier einzelner Systeme zu addieren und sie mit der eines Systems zu vergleichen, dessen Größe beide zusammen haben.

Die Lösung des Paradoxons führt zu der Feststellung, dass die Teilchen, aus denen das System besteht, nicht unterscheidbar sein müssen. Dies führt dazu, dass es bei der Interaktion nicht möglich ist zu wissen, welche welcher entspricht, was bedeutet, dass neue Alternativen geschaffen werden:

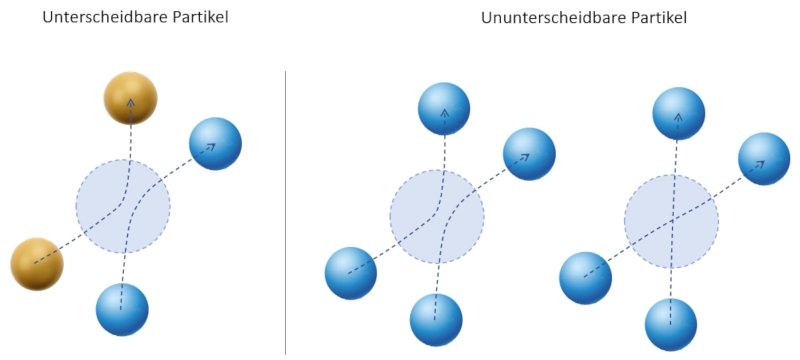
Die neuen Alternativen entsprechen zusätzlichen Informationen, die zur Definition der möglichen Zustände benötigt werden.

Hinweis: Derek Muller-Video von Veritasiums untersucht den quantenmechanischen Effekt, ohne auf das Gibbs-Paradoxon hinzuweisen.

ID:(13044, 0)

Bild

>Top

Die statistische Mechanik versucht nicht, die Bewegungsgleichungen des Systems zu lösen. Es versucht zu erkennen, wie die Bewegungsgleichungen die möglichen Zustände begrenzen, und allgemeine Muster zu erkennen, die es ermöglichen, den Zustand des Systems und seine Entwicklung zu beschreiben.

In Analogie zu einem Bild ist die Situation der maximalen Information (Entropie) und des perfekten Chaos ein Rahmen von zufällig ausgewählten Pixeln.

Ein reales System hat eine Struktur, eine Ordnung, die in Analogie zum Gemälde einem Bild entsprechen würde, in dem Strukturen wie die Gruppierung von Farben erkannt werden. Variationen innerhalb dieser Pixel werden nicht erkannt, da dies ein äquivalenter Rahmen für den Beobachter ist. Das Analoge tritt in einem physikalischen System auf, in dem es mehrere Variationen der Bedingungen gibt, die denselben Makrozustand des Systems beschreiben. In diesem Sinne

Die statistische Mechanik untersucht Zusammenstellungen (Mengen) möglicher Zustände auf der Grundlage makroskopischer Parameter, die sie begrenzen und ihre Existenzwahrscheinlichkeit bestimmen.

ID:(13045, 0)

Beschreibung

>Top

Die zahlreichen Alternativen, die 10^{23} -Partikel bedeuten, befinden sich auf mikroskopischer Ebene.

Viele dieser mikroskopischen Zustände sind jedoch auf makroskopischer Ebene sehr ähnlich, wenn nicht sogar identisch.

Wenn es am Ende nur eine diskrete Anzahl möglicher makroskopischer Zustände gibt, kann seine Existenzwahrscheinlichkeit als Funktion der Anzahl der damit verbundenen mikroskopischen Zustände geschätzt werden.

Auf diese Weise löst die statistische Mechanik das Problem

• Bestimmen der möglichen mikroskopischen Zustände

• Bestimmen der makroskopischen Zustände, die den mikroskopischen Zuständen zugeordnet sind

• Bestimmen durch die Anzahl der mikroskopischen Zustände die Wahrscheinlichkeit jedes makroskopischen Zustands

ID:(11400, 0)

Beschreibung

>Top

Wenn wir versuchen, den Zustand des Systems von 10^{23} -Partikeln zu beschreiben, greifen wir auf die Mechanik zurück, um die Gleichungen zu erstellen, die die möglichen physikalischen Zustände des Systems definieren.

Dafür:

mögliche Zustände werden im Phasensystem p-q berücksichtigt

Die Einschränkungen, die für die möglichen Zustände bestehen, werden untersucht (Beispiel bei gegebener Gesamtenergie).

Es wird versucht, Methoden in der Lage zu sein, die Anzahl der Zustände zu zählen, die unter den gegebenen Einschränkungen existieren

ID:(11401, 0)

Beschreibung

>Top

Um die möglichen makroskopischen Zustände und die Häufigkeit zu erhalten, ist es notwendig, eine statistische Analyse zu entwickeln :.

• Bestimmen Sie die Wahrscheinlichkeitsverteilung für jeden makroskopischen Zustand

• Untersuchen Sie, wie sich die Verteilung in Abhängigkeit von den makroskopischen Parametern des Systems entwickelt

• In den meisten Fällen ist das Ergebnis, dass ein makroskopischer Zustand mit hoher Wahrscheinlichkeit vorliegt und

• Die Verteilung liefert Informationen über die Dispersion, die die verschiedenen Parameter haben können

ID:(11402, 0)

0

Video

Video: Was ist statistische Mechanik?