Ley de Snell
Storyboard 
La ley de Snell permite determinar el angulo con que un haz de luz se refracta (desvía) en función de las características de ambos medios.
Las características de ambos medios se refieren al indice de refracción o a la velocidad de propagación en el respectivo medio.
ID:(302, 0)
Paso entre medios de distintas velocidad de la luz
Definición 
Cuando la luz en un medio con velocidad de la luz
La transmisión sin embargo no solo puede perder intensidad, por la fracción reflejada, también puede ser desviada. Este desvío se denomina refracción.
ID:(429, 0)
Principio de Huygens: refracción de la luz
Imagen 
Para aplicar el principio de Huygens en el caso del paso de luz de un medio a un segundo en que la velocidad de la luz varia, se debe considerar fuentes que gatillada en el primero y genera ondas esféricas en el segundo:
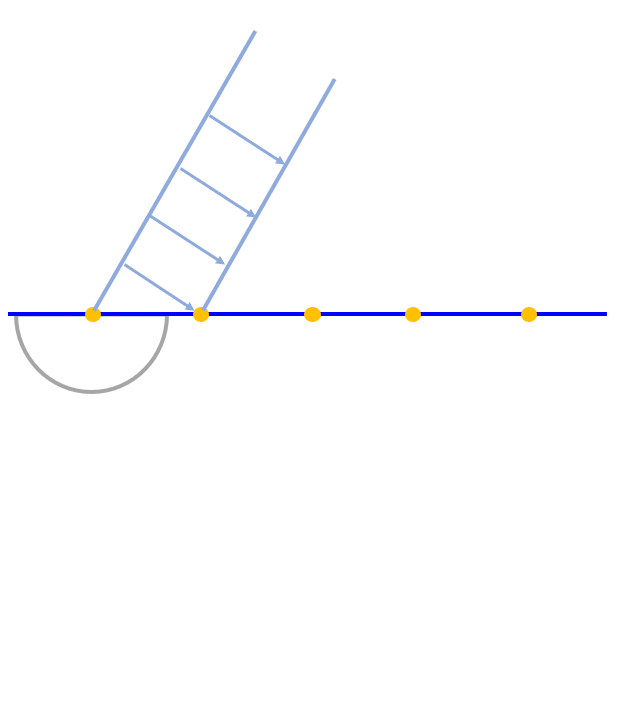
ID:(12667, 0)
Principio de Huygens: creación de segunda fuente y radiación de la primera
Nota 
A medida que se crea la segunda fuente la primera ya ha irradiado:
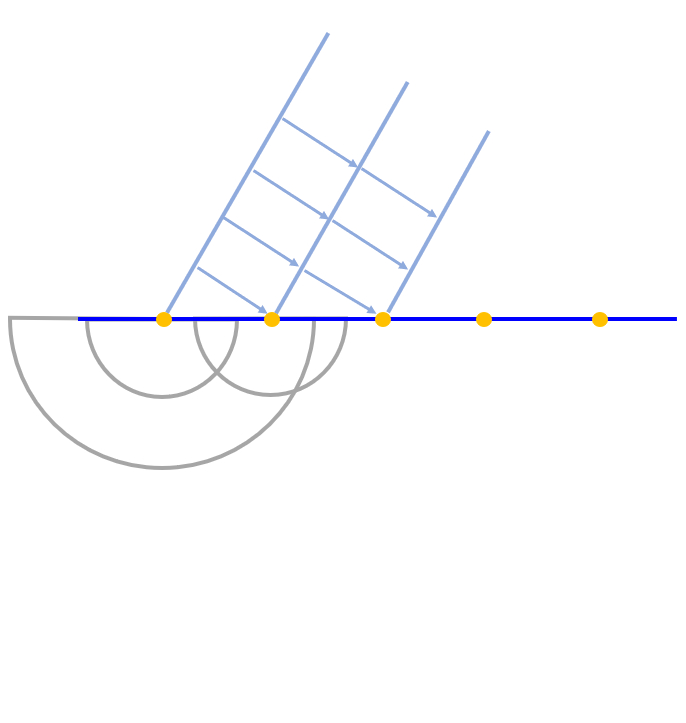
Eso si se debe tener presente que al ser las velocidades distintas el tamaño de la radiación esférica es de diferente tamaño en los dos medios.
ID:(12668, 0)
Principio de Huygens: nuevas fuentes y mas radiación en el segundo medio
Cita 
Continuando se va viendo como se comienza a generar un nuevo frente de onda que no presenta la misma orientación que el primero:
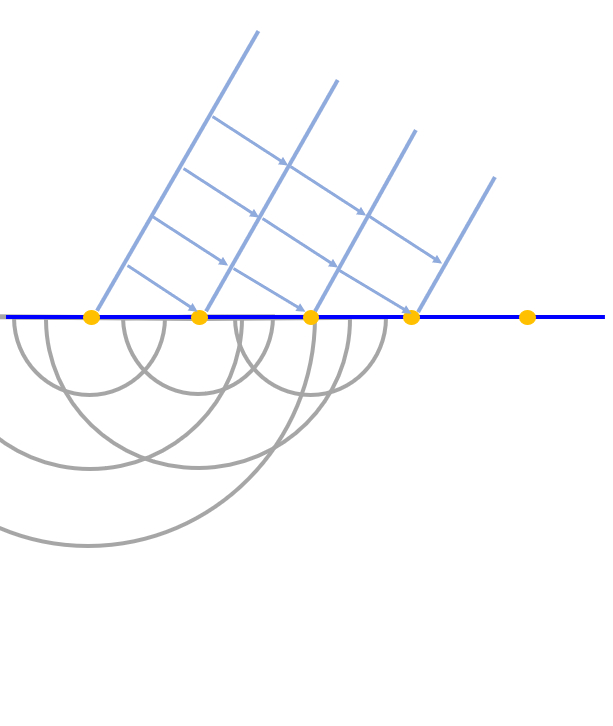
ID:(12669, 0)
Principio de Huygens: el cambio en el frente de onda
Ejercicio 
Finalmente se pueden dibujar los frentes de onda quedando claro que la dirección de propagación ha cambiado:
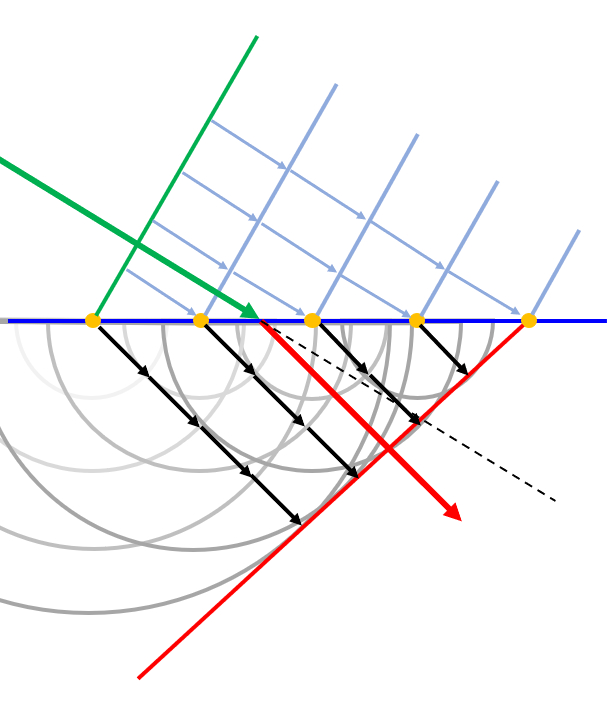
Esto se denomina la refracción de la luz.
ID:(12670, 0)
Relación de angulo entre haz incidente y haz transmitido
Ecuación 
Del principio de Huygens se puede establecer la relación entre los ángulos de incidencia y el de transmisión:
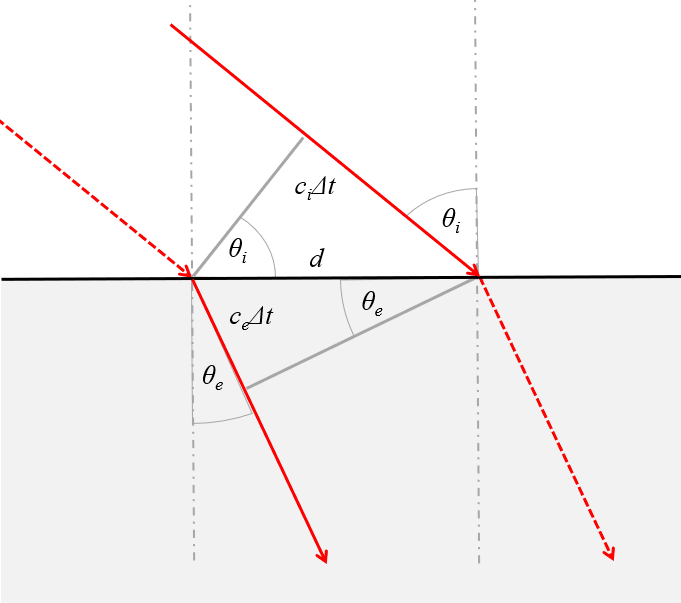
Se ve claramente que la diferencia se da justamente por el efecto de la variación de la velocidad de la luz en cada medio.
ID:(12672, 0)
Refracción de haces de luz de vacio a medio
Variable 
Paso de medio con mayor a menor velocidad
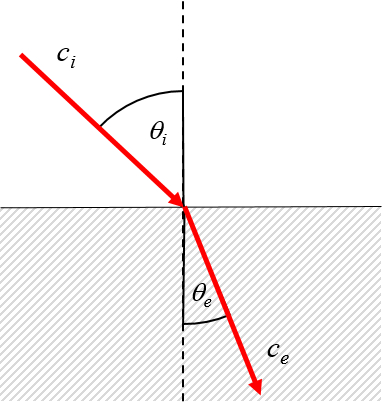
Paso del vacío, donde la velocidad de la luz es
ID:(1849, 0)
Refracción de haces de luz de medio a vacio
Audio 
Cuando un haz pasa de un medio de menor velocidad
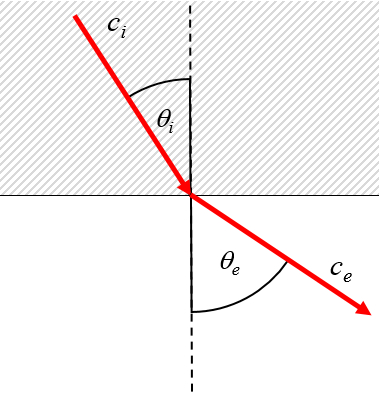
Paso de un medio, donde la velocidad de la luz
ID:(1850, 0)
Medición de la ley de Snell
Video 
Para confirmar empiricamente la ley de Snell se usa un banco optico:
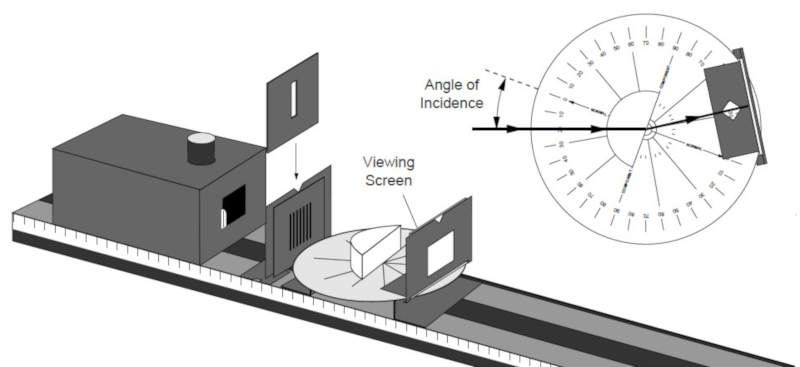
Los banco ópticos son barras largas en que se pueden montar
• fuentes de luz
• colimadores (placas con rendijas)
• espejos planos y curvos
• prismas y lentes
ID:(12671, 0)
Medición del haz refractado
Unidad 
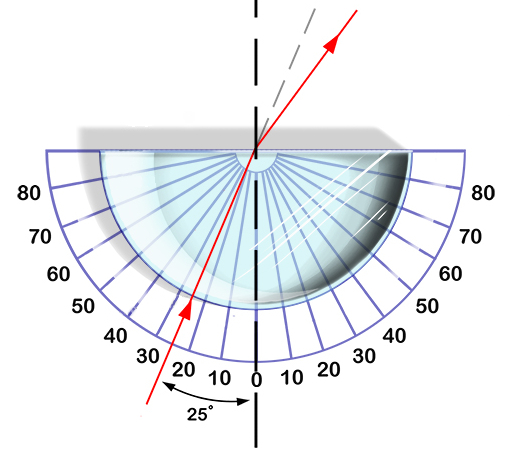
Para mostrar/estudiar la refracción se usa un vidrio que por un lado es curvo. Esto permite girar el vidrio sin que su superficie deje de estar perpendicular al haz por lo que ingresa sin refracción. De esta forma se puede ver como el haz se refracta en la interface vidrio-aire:

ID:(12673, 0)
Ley de Snell
Descripción 
La ley de Snell permite determinar el angulo con que un haz de luz se refracta (desvía) en función de las características de ambos medios. Las características de ambos medios se refieren al indice de refracción o a la velocidad de propagación en el respectivo medio.
Variables
Cálculos
Cálculos
Ecuaciones
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
(ID 3342)
Como la relaci n entre los ngulos de incidencia y refracci n es
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
y el indice de refracci n se define como
| $ n =\displaystyle\frac{ c }{ v }$ |
\\n\\nse tiene que con\\n\\n
$n_i=\displaystyle\frac{c}{c_i}$
y\\n\\n
$n_e=\displaystyle\frac{c}{c_e}$
\\n\\nque\\n\\n
$\displaystyle\frac{c_i}{c_e}=\displaystyle\frac{c_i}{c}\displaystyle\frac{c}{c_e}=\displaystyle\frac{n_e}{n_i}=\displaystyle\frac{\sin\theta_i}{\sin\theta_e}$
por lo que resulta
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
(ID 3343)
La energ a de una onda o part cula de luz, representada por el fot n, est definida como
| $ \epsilon = h \nu $ |
Cuando esta energ a se propaga de un medio, como el vac o, con una velocidad de la luz $c$, a otro medio con una velocidad de la luz $c_m$, se concluye que la frecuencia de la luz no cambia. Sin embargo, esto implica que, dado que la velocidad de la luz es igual al producto de la frecuencia y la longitud de onda, como se muestra en la ecuaci n
| $ c = \nu \lambda $ |
la longitud de onda debe ajustarse conforme cambia el medio.
Por lo tanto, si consideramos una longitud de onda de la luz en un medio $\lambda_m$ y en el vac o $\lambda$, podemos expresar el ndice de refracci n como
| $ n =\displaystyle\frac{ c }{ v }$ |
y se puede escribir de la siguiente manera:
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
En resumen,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
Ejemplos
Cuando la luz en un medio con velocidad de la luz
La transmisi n sin embargo no solo puede perder intensidad, por la fracci n reflejada, tambi n puede ser desviada. Este desv o se denomina refracci n.
(ID 429)
Para aplicar el principio de Huygens en el caso del paso de luz de un medio a un segundo en que la velocidad de la luz varia, se debe considerar fuentes que gatillada en el primero y genera ondas esf ricas en el segundo:

(ID 12667)
Si $n$ representa el ndice de refracci n en un medio y $\lambda$ es la longitud de onda en el vac o, entonces al propagarse en el medio, la longitud de onda $\lambda_m$ ser
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
A medida que se crea la segunda fuente la primera ya ha irradiado:

Eso si se debe tener presente que al ser las velocidades distintas el tama o de la radiaci n esf rica es de diferente tama o en los dos medios.
(ID 12668)
Continuando se va viendo como se comienza a generar un nuevo frente de onda que no presenta la misma orientaci n que el primero:

(ID 12669)
Finalmente se pueden dibujar los frentes de onda quedando claro que la direcci n de propagaci n ha cambiado:

Esto se denomina la refracci n de la luz.
(ID 12670)
Del principio de Huygens se puede establecer la relaci n entre los ngulos de incidencia y el de transmisi n:

Se ve claramente que la diferencia se da justamente por el efecto de la variaci n de la velocidad de la luz en cada medio.
(ID 12672)
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica

se pueden escribir en funci n de la velocidad de la luz en cada medio
| $\displaystyle\frac{ \sin \theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
(ID 3342)
La ley de Snell para el paso de la luz de un medio de indice
| $ n_i \sin \theta_i = n_e \sin \theta_r $ |
(ID 3343)
El ndice de refracci n, representado como $n$, se define como la raz n entre la velocidad de la luz en el vac o, representada como $c$, y la velocidad de la luz en el medio, representada como $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
(ID 3192)
Paso de la luz por un objeto
Paso por un vidrio
(ID 1853)
Paso de medio con mayor a menor velocidad

Paso del vac o, donde la velocidad de la luz es
(ID 1849)
Cuando un haz pasa de un medio de menor velocidad

Paso de un medio, donde la velocidad de la luz
(ID 1850)
Para confirmar empiricamente la ley de Snell se usa un banco optico:

Los banco pticos son barras largas en que se pueden montar
• fuentes de luz
• colimadores (placas con rendijas)
• espejos planos y curvos
• prismas y lentes
(ID 12671)
Para mostrar/estudiar la refracci n se usa un vidrio que por un lado es curvo. Esto permite girar el vidrio sin que su superficie deje de estar perpendicular al haz por lo que ingresa sin refracci n. De esta forma se puede ver como el haz se refracta en la interface vidrio-aire:

(ID 12673)
ID:(302, 0)
