Usuario:


Reflexión Total
Storyboard

Cuando la luz pasa de un medio con alto indice de refracción (baja velocidad) a uno de menor indice de refracción (mayor velocidad) el haz se refracta en un angulo mayor respecto de la normal de la interface. Eso lleva a que para un cierto angulo de incidencia finito el anglo de refracción alcanza 90 grados haciendo imposible que el haz pase al segundo medio. Eso lleva a que el haz experimente una refracción interna total.

>Modelo

ID:(1262, 0)


Paso entre medios de distintas velocidad de la luz
Definición

Cuando la luz en un medio con velocidad de la luz c_i alcanza una medio con una velocidad de la luz c_e el haz en en parte reflejado y en parte transmitido.

La transmisión sin embargo no solo puede perder intensidad, por la fracción reflejada, también puede ser desviada. Este desvío se denomina refracción.

ID:(429, 0)


Refracción de haces de luz de vacio a medio
Imagen

Paso de medio con mayor a menor velocidad

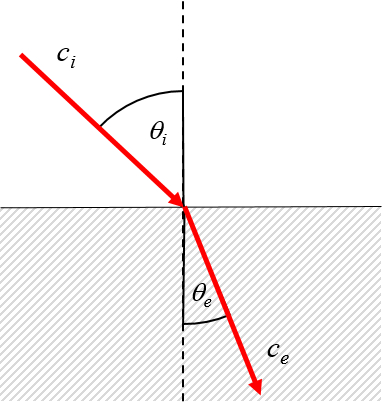
Paso del vacío, donde la velocidad de la luz es c a un medio con velocidad v

ID:(1849, 0)


Refracción de haces de luz de medio a vacio
Nota

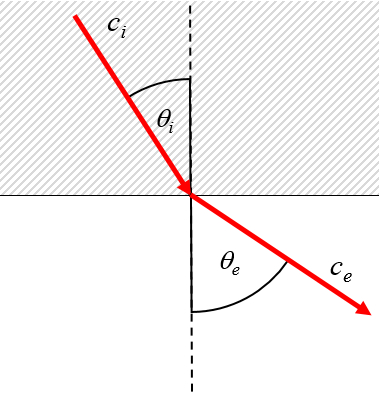
Cuando un haz pasa de un medio de menor velocidad v_i a uno con mayor v_e su dirección se altera de modo que el angulo de incidencia \theta_i se agranda:

Paso de un medio, donde la velocidad de la luz v, al vacío.

ID:(1850, 0)


Reflexión total
Cita

Cuando se pasa de un medio en que la velocidad de la luz es menor a uno que es mayor existe la situación de que a un ángulo de incidencia muy grande no existe un correspondiente angulo de refracción. En estos casos la luz solo se refleja y hablamos de reflexión total.

En la siguiente imagen se ven distintos haces que al llegar a ser muy grande el angulo comienzan a sufrir reflexión total:

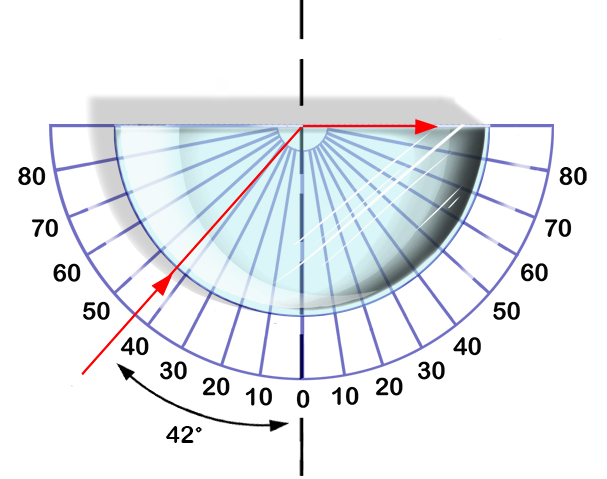
Paso por un vidrio

ID:(1851, 0)


Reflexión total en agua según un buso
Ejercicio

Si el haz en un medio de menos velocidad trata de pasar a un medio de mayor velocidad en un angulo tal que no existe un angulo de refracción este es totalmente reflejado en la interface entre ambos medios.

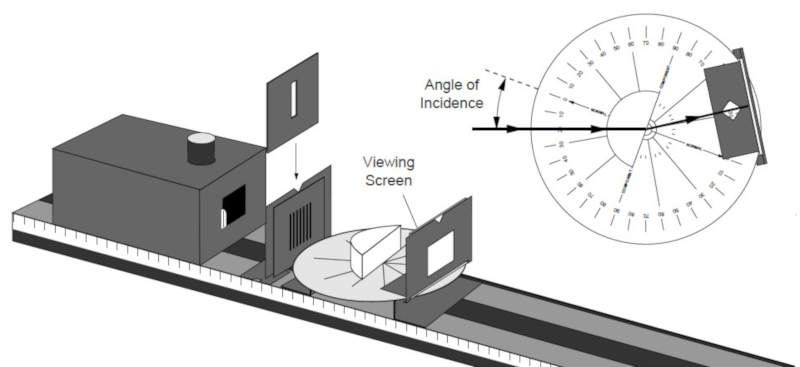
ID:(1852, 0)


Observando la refracción total
Ecuación

En el caso de que se pase de un sistema de menor a mayor velocidad existe la situación en que el haz transmitido, que tiene que ser siempre mayor al incidente, llegue a ser 90 grados. Si en esa situación se continua aumentando el angulo de incidencia se observara que el haz comienza a reflejarse bajo el mismo angulo que incidió:

Este fenómeno se denomina refracción total.

ID:(12675, 0)


Refracción total en el agua
Script

Si consideramos lo que vera un buso debajo del agua veremos que ...

• Existe un cono en que no existe refracción total que esta sobre el. Esto porque al mirar hacia arriba la luz que viene dentro del agua logra 'escapar' porque su angulo respecto de la normal es menor que el angulo critico. Por esta razón en esta dirección vemos lo que esta fuera del agua.
• Fuera del cono todo lo que esta dentro del agua se refleja en la superficie. Esta opera como un espejo mostrando todo en forma invertida y se superpone con lo que se ve dentro del agua (como por ejemplo la ola en la superficie).
&bull: Adicional a lo que se ve reflejado en la superficie el buzo ve lo que esta dentro del agua.

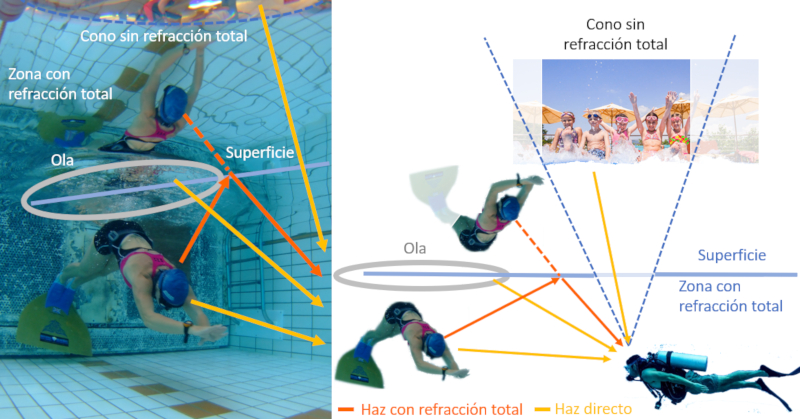
Como la velocidad de la luz en el agua es 2.2541e+8 m/s y en el aire 2.9979e+8 m/s es se puede calcular el angulo de refracción total. Este resulta con un valor de 48.5 lo que muestra que el cono es una sección no menor de la superficie.

ID:(12680, 0)


Energía Total
Descripción

La energía total es la suma de la energía cinética total y la energía potencial donde la energía cinética total es la suma de la energía cinética de traslación y rotación.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$z$
z
Altura sobre el suelo
m
$Q$
Q
Calor disipado
$E$
E
Energía
J
$K_i$
K_i
Energía cinética 1
J
$K$
K
Energía cinética total
J
$V$
V
Energía potencial
J
$U_i$
U_i
Energía potencial 1
J
$E$
E
Energía total
J
$v$
v
Velocidad
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Cuando un objeto se eleva a una altura $h$, gana energ a potencial

$ V = - m_g g z $



Si el objeto comienza a caer, la energ a potencial se transformar en energ a cin tica:

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$



En el momento en que el objeto llega al suelo ($h=0$), toda la energ a potencial se ha convertido en cin tica, lo que lleva a la ecuaci n:

$\displaystyle\frac{m}{2}v^2=mgh$



Si se despeja la velocidad, se obtiene:

$ v =\sqrt{2 g h }$

(ID 9903)

Ejemplos

La energía total ($E$) corresponde a la suma de la energía cinética total ($K$) y la energía potencial ($V$):

$ E = K + V $

(ID 3687)

Cuando se presenta fricci n, observamos que los cuerpos se calientan, por lo que tiene sentido hablar de energ a t rmica. En estos casos, la energ a total

$ E = K + V $



no parece conservarse a menos que interpretemos el calor generado como otra forma de energ a. Mohr fue el primero en darse cuenta de que la suma de las energ as cin tica $K$, potencial $V$ y t rmica $Q$ se conserva

$ E = K + U + Q $

y solo existen conversiones entre estas formas.

(ID 3247)

En un sistema m s complejo, la energ a cin tica total es igual a la suma de las energ as cin ticas de las partes individuales

$ K = \displaystyle\sum_i K_i $

(ID 7149)

En un sistema más complejo, la energ a potencial total es igual a la suma de las energ as potenciales de las partes individuales

$ V =\displaystyle\sum_i V_i $

(ID 7150)

Un objeto que se eleva a una altura $h$ gana energ a potencial

$ V = - m_g g z $



Si el objeto comienza a caer, la energ a potencial se transformar en energ a cin tica,

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$



por lo que la velocidad con la que impacta el suelo es:

$ v =\sqrt{2 g h }$

(ID 9903)

ID:(1423, 0)