User: 
Light Interference from two Sources
Storyboard 
When light from two sources or grooves is superimposed, points are observed in the space in which there is constructive and other destructive interference generating areas of greater intensity or zero intensity.
ID:(1271, 0)
El concepto de interferencia
Image
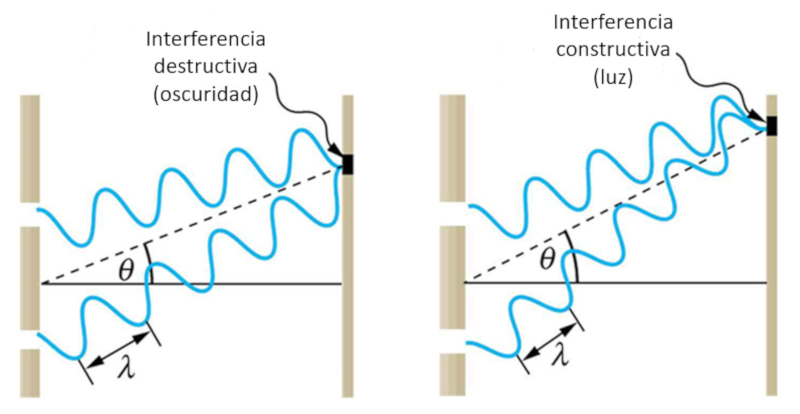
La interferencia ocurre cuando dos haces se superponen en un punto del espacio y con ello sus amplitudes se suman. Esto puede llevar a
• ambas tienen fases similares con lo que sus amplitudes son ambas positivas o negativas lo que lleva a una interferencia constructiva y a un aumento de la señal
• las fases difieren de modo que los signos de las amplitudes son mayormente distintos con lo que la interferencia es destructiva y la señal se reduce e incluso puede anularse
ID:(12495, 0)
El caso de dos rentijas
Image
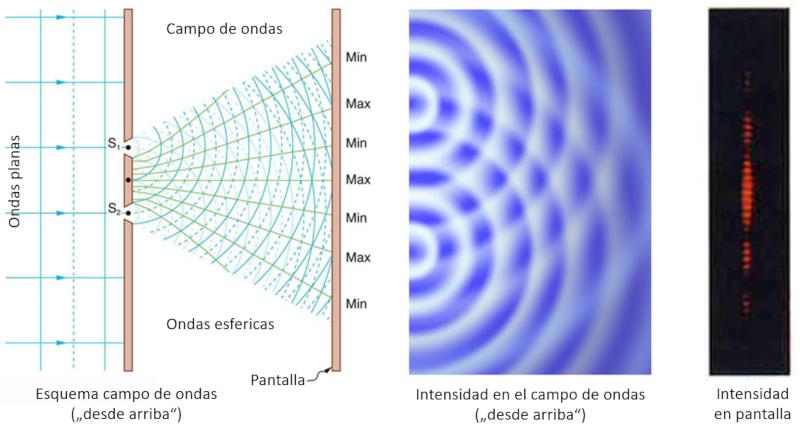
Cuando se tienen dos rendijas se puede observar como la onda plana pasa a generar dos ondas esféricas que generan un campo de onda en que se observan las distintas interferencias. Si se localiza a alguna distancia una pantalla se puede observar el perfil de dichas interferencias creándose casos de interferencia constructiva como destructiva:
ID:(12496, 0)
Calculo de la interferencia en la pantalla
Image
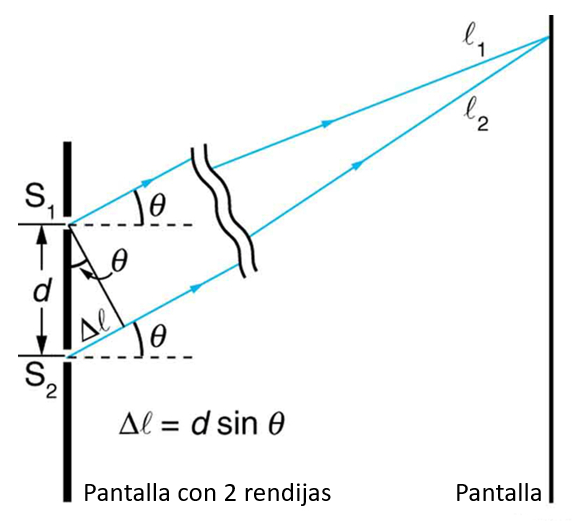
Si se asume que la pantalla se encuentra a una distancia mucho mayor que aquella entre ambas fuentes (rendijas) se puede estimar el desface de ambas señales en forma relativamente simple:
ID:(12497, 0)
Patrón de interferencia
Image
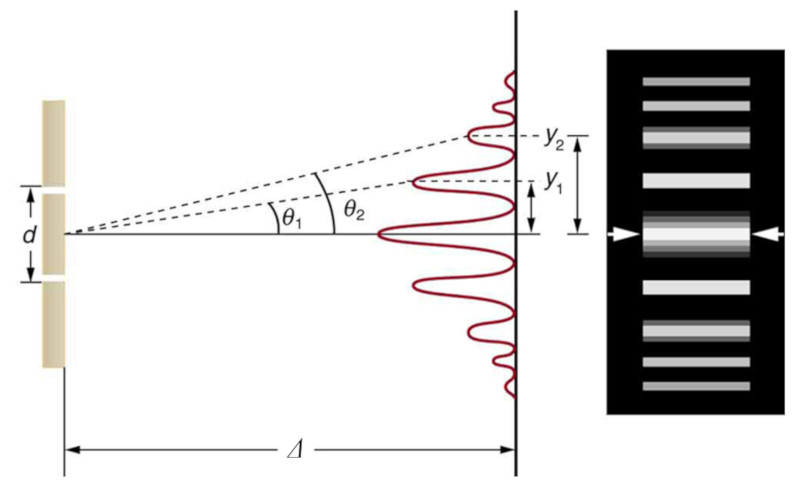
Si se diagrama la intensidad registrada en la pantalla se vera lo que se denomina el típico patrón de interferencia:
ID:(12498, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
\left( n_d + \displaystyle\frac{1}{2}\right) \lambda = d \sin \theta_d
( n_d + 1/2)* lambda = d *sin( theta_d )
I = I_0 \cos^2 \displaystyle\frac{ \phi }{2}
I = I_0 *cos( phi /2)^2
n_c \lambda = d \sin \theta_c
n_c * lambda = d * sin( theta_c )
\phi =\displaystyle\frac{2 \pi }{ \lambda }( r_2 - r_1 )
phi =2* pi *( r_2 - r_1 )/ lambda
y_m =\displaystyle\frac{ \Delta }{ d } n_c \lambda
y_m = Delta * n_c * lambda / d
ID:(16082, 0)
Constructive interference with two sources
Equation
Para que la interferencia sea constructiva es necesario que la diferencia de camino sea un múltiplo de el largo de onda\\n\\n
\Delta l = n \lambda
\\n\\nPor ello, como el largo es el cateto opuesto de un triangulo en que la hipotenusa es igual a la distancia entre ambas fuentes o rendijas se tiene\\n\\n
\Delta l = d \sin\theta
De ambas ecuaciones se tiene entonces que
| n_c \lambda = d \sin \theta_c |
ID:(10938, 0)
Destructive interference with two sources
Equation
Para que la interferencia sea destructiva es necesario que la diferencia de camino sea un múltiple mas un medio del largo de onda\\n\\n
\Delta l =\left( n + \displaystyle\frac{1}{2}\right) \lambda
\\n\\nPor ello, como el largo es el cateto opuesto de un triangulo en que la hipotenusa es igual a la distancia entre ambas fuentes o rendijas se tiene\\n\\n
\Delta l = d \sin\theta
De ambas ecuaciones se tiene entonces que
| \left( n_d + \displaystyle\frac{1}{2}\right) \lambda = d \sin \theta_d |
ID:(10939, 0)
Shiny girdle position
Equation
Con la distancia
\tan\theta_n = \displaystyle\frac{y_n}{\Delta}
\\n\\nPara ángulos pequeños la función tangente se puede aproximar por el seno\\n\\n
\tan \theta_n \sim \sin \theta_n
por lo que la posición de los máximo es
| n_c \lambda = d \sin \theta_c |
por lo que las posiciones de los máximos es
| y_m =\displaystyle\frac{ \Delta }{ d } n_c \lambda |
ID:(10940, 0)
Intensity in one position
Equation
Si que existe un desfase
| \phi =\displaystyle\frac{2 \pi }{ \lambda }( r_2 - r_1 ) |
se tendrá que la intensidad es igual a
| I = I_0 \cos^2 \displaystyle\frac{ \phi }{2} |
ID:(10941, 0)
Phase difference
Equation
La diferencia de fase de da por la diferencia en los caminos recorridos. Si se denotan se tendra que
| \phi =\displaystyle\frac{2 \pi }{ \lambda }( r_2 - r_1 ) |
ID:(10942, 0)
0
Video
Video: Interferencia de la luz de dos Fuentes