User:
Interference in Thin Films
Storyboard 
When light from two sources or grooves is superimposed, points are observed in the space in which there is constructive and other destructive interference generating areas of greater intensity or zero intensity.
ID:(1272, 0)
Interferencia en películas delgadas
Image
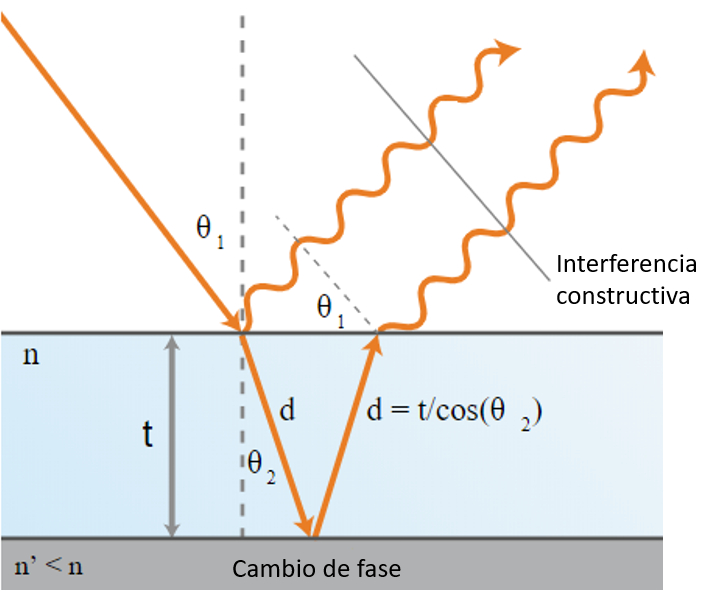
En una película semitransparente para el tipo de onda empelada esta sera parcialmente reflejada en la superficie mientras que la parte transmitida lo sera en el borde inferior. De esta forma interferir las ondas reflejadas desde la superficie con aquellas en el otro borde de la película permitiendo por ejemplo medir el grosor de la película:
ID:(12499, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$
lambda_cc =(2* h_c )/( n_cc +1/2)
$ \lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c $
lambda_cd =(2* h_c )/ n_cd
$ \lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s $
lambda_sc =(2* h_s )/ n_sc
$ \lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$
lambda_sd =(2* h_s )/( n_sd +1/2)
ID:(16083, 0)
Constructive reflection without lag
Equation
En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia constructiva es igual a
| $ \lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s $ |
ID:(10943, 0)
Destructive reflection without lag
Equation
En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia destructiva es igual a
| $ \lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$ |
ID:(10944, 0)
Constructive reflection with lag
Equation
En el caso de que la reflexión sufra un desfase en
| $ \lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$ |
ID:(10945, 0)
Destructive reflection with lag
Equation
En el caso de que la reflexión sufra un desfase en
| $ \lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c $ |
ID:(10946, 0)
0
Video
Video: Interferencia en Películas Delgadas