Druyd:Knowledge

Interferencia en Películas Delgadas

Storyboard

En el caso de una película delgada una parte de la luz que incide se refleja en forma directa. El resto penetra la película, reflejándose en el borde inferior, volviendo a la superficie en donde interfiere la luz reflejada en forma directa. Esto genera un parón de interferencia con lineas de interferencia constructivas (luz) y otras destructivas (oscuridad).

>Modelo

ID:(1272, 0)

Mecanismos

Iframe

>Top

Conocimiento

Código

Concepto

Mecanismos

ID:(16089, 0)

Interferencia en películas delgadas

Imagen

>Top

En una película semitransparente para el tipo de onda empelada esta sera parcialmente reflejada en la superficie mientras que la parte transmitida lo sera en el borde inferior. De esta forma interferir las ondas reflejadas desde la superficie con aquellas en el otro borde de la película permitiendo por ejemplo medir el grosor de la película:

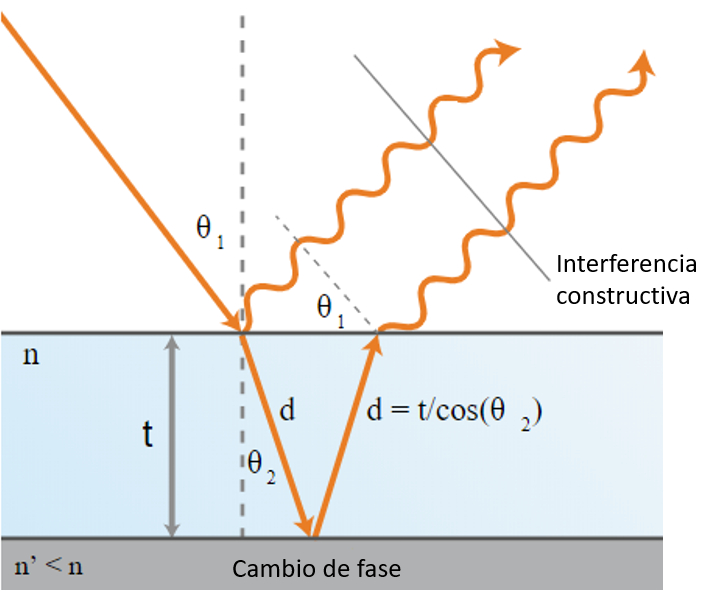
ID:(12499, 0)

Modelo

Top

>Top

Parámetros

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$h_c$

h_c

Grosor de la película con desfase

$h_s$

h_s

Grosor de la película sin desfase

$\lambda$

lambda

Largo de onda de luz visible

$n_{cc}$

n_cc

Número de línea de interferencia constructiva película con desfase

$n_{sc}$

n_sc

Número de línea de interferencia constructiva película sin desfase

$n_{cd}$

n_cd

Número de línea de interferencia destructiva película con desfase

$n_{sd}$

n_sd

Número de línea de interferencia destructiva película sin desfase

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

Ecuación

$\lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$

lambda_cc =(2* h_c )/( n_cc +1/2)

$\lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c$

lambda_cd =(2* h_c )/ n_cd

$\lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s$

lambda_sc =(2* h_s )/ n_sc

$\lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$

lambda_sd =(2* h_s )/( n_sd +1/2)

ID:(16083, 0)

Reflexión constructiva sin desfase

Ecuación

>Top, >Modelo

En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia constructiva es igual a

$\lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s$

$h_s$

Grosor de la película sin desfase

$m$

8447

$\lambda_{sc}$

Largo de onda de luz visible

$m$

8439

$n_{sc}$

Número de línea de interferencia constructiva película sin desfase

$-$

8461

ID:(10943, 0)

Reflexión destructiva sin desfase

Ecuación

>Top, >Modelo

En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia destructiva es igual a

$\lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$

$h_s$

Grosor de la película sin desfase

$m$

8447

$\lambda_{sd}$

Largo de onda de luz visible

$m$

8439

$n_{sd}$

Número de línea de interferencia destructiva película sin desfase

$-$

8462

ID:(10944, 0)

Reflexión constructiva con desfase

Ecuación

>Top, >Modelo

En el caso de que la reflexión sufra un desfase en \pi la condición para que exista interferencia constructiva es igual a

$\lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$

$h_c$

Grosor de la película con desfase

$m$

8465

$\lambda_{cc}$

Largo de onda de luz visible

$m$

8439

$n_{cc}$

Número de línea de interferencia constructiva película con desfase

$-$

8463

ID:(10945, 0)

Reflexión destructiva con desfase

Ecuación

>Top, >Modelo

En el caso de que la reflexión sufra un desfase en \pi la condición para que exista interferencia destructiva es igual a

$\lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c$

$h_c$

Grosor de la película con desfase

$m$

8465

$\lambda_{cd}$

Largo de onda de luz visible

$m$

8439

$n_{cd}$

Número de línea de interferencia destructiva película con desfase

$-$

8464

ID:(10946, 0)

0

Video

Video: Interferencia en Películas Delgadas