Benützer:
Interferenz in Dünnen Filmen
Storyboard 
Wenn sich Licht von zwei Quellen oder Rillen überlappt, werden Punkte in dem Raum beobachtet, in dem konstruktive und andere zerstörerische Interferenz erzeugende Bereiche größerer Intensität oder Nullintensität vorhanden sind.
ID:(1272, 0)
Interferencia en películas delgadas
Bild
En una película semitransparente para el tipo de onda empelada esta sera parcialmente reflejada en la superficie mientras que la parte transmitida lo sera en el borde inferior. De esta forma interferir las ondas reflejadas desde la superficie con aquellas en el otro borde de la película permitiendo por ejemplo medir el grosor de la película:
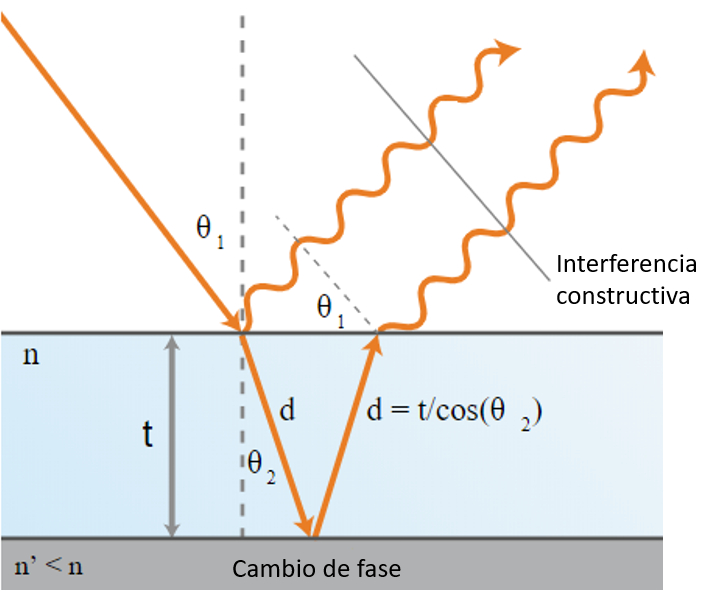
ID:(12499, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$
lambda_cc =(2* h_c )/( n_cc +1/2)
$ \lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c $
lambda_cd =(2* h_c )/ n_cd
$ \lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s $
lambda_sc =(2* h_s )/ n_sc
$ \lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$
lambda_sd =(2* h_s )/( n_sd +1/2)
ID:(16083, 0)
Konstruktive Reflexion ohne Verzögerung
Gleichung
En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia constructiva es igual a
| $ \lambda_{sc} =\displaystyle\frac{2}{ n_{sc} } h_s $ |
ID:(10943, 0)
Destruktive Reflexion ohne Verzögerung
Gleichung
En el caso de que la reflexión no sufra un desfase, la condición para que exista interferencia destructiva es igual a
| $ \lambda_{sd} =\displaystyle\frac{2 h_s }{ n_{sd} +\displaystyle\frac{1}{2}}$ |
ID:(10944, 0)
Konstruktive Reflexion mit Verzögerung
Gleichung
En el caso de que la reflexión sufra un desfase en
| $ \lambda_{cc} =\displaystyle\frac{2 h_c }{ n_{cc} +\displaystyle\frac{1}{2}}$ |
ID:(10945, 0)
Destruktive Reflexion mit Verzögerung
Gleichung
En el caso de que la reflexión sufra un desfase en
| $ \lambda_{cd} =\displaystyle\frac{2}{ n_{cd} } h_c $ |
ID:(10946, 0)
0
Video
Video: Interferencia en Películas Delgadas