User:
Diffraction by a Slit
Storyboard 
When passing a beam of light through a slit, it appears at the diffraction edges. This can be modeled on Huygens' principle that there are sources at the edges of the slits that radiate sideways to an area where a rectilinear beam would not access.
ID:(1379, 0)
Luz por una rendija, difracción
Image
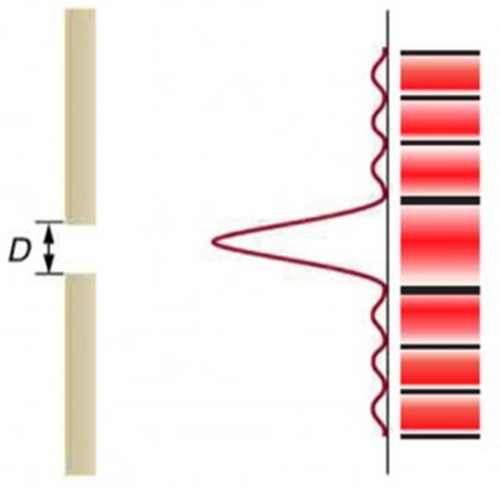
Si uno tiene una sola rendija y se aleja suficiente se observa algo curioso: aparece nuevamente el patrón de interferencia pese a que no hay una segunda fuente para generar interferencia.
ID:(12500, 0)
Propagación por la curva
Image
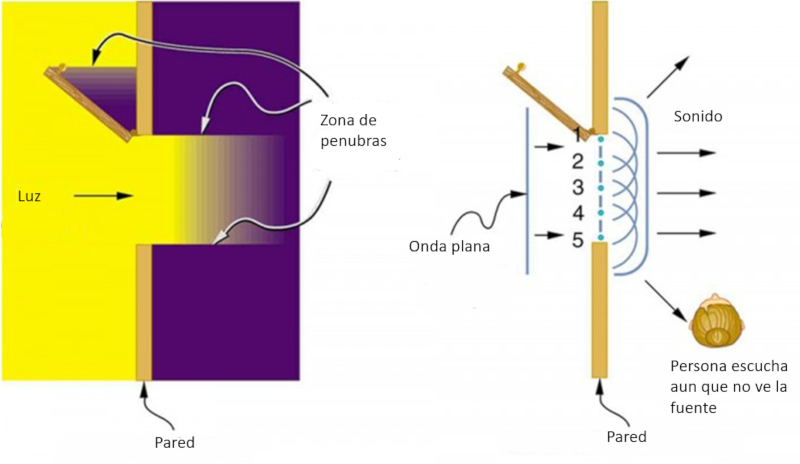
Uno de los fenómenos curiosos de las ondas es que son capaces de propagar detrás de un objeto. Dependiendo del tamaño del largo de la onda el objeto afecta o no a la onda: si es mas pequeña tendera a crear sombras mientras si es mas grande incurrirá en la zona detrás.
ID:(12440, 0)
Calculo de la luz por una rendija
Image
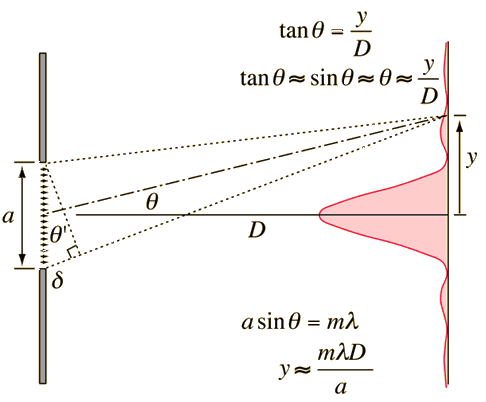
Si se modela con el principio de Huygens como una cadena de fuentes se puede estimar la interferencia y obtener la expresión del patrón de interferencia para lo que es una rendija única.
ID:(12501, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ I = I_0 \left[\displaystyle\frac{sin( \pi m )}{ \pi m }\right]^2$
I = I_0 *[sin( pi * m )/( pi * m )]^2
$ \lambda =\displaystyle\frac{ a \sin \theta }{ m }$
lambda = a *sin( theta )/ m
ID:(16086, 0)
Difracción en una rejilla
Equation
La diferencia de camino se puede estimar con el ancho de la ranura que corresponde a la hipotenusa del triangulo que define el desface y el angulo en la dirección que observamos la pantalla. Con ello se obtiene que
| $ \lambda =\displaystyle\frac{ a \sin \theta }{ m }$ |
ID:(10947, 0)
Intensidad en difracción en rendija
Equation
Con el desfase por la dirección en que la luz llega a la pantalla se puede estimar la intensidad de esta.
En tal caso se obtiene
| $ I = I_0 \left[\displaystyle\frac{sin( \pi m )}{ \pi m }\right]^2$ |
ID:(10948, 0)
0
Video
Video: Difracción por una Rendija