Utilisateur:
Loi du levier
Description 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3241)
(ID 3241)
Dans le cas d'une balance, une force gravitationnelle agit sur chaque bras, g n rant un couple
| $ T = r F $ |
Si les longueurs des bras sont $d_i$ et les forces sont $F_i$ avec $i=1,2$, la condition d' quilibre exige que la somme des couples soit nulle :
| $\displaystyle\sum_i \vec{T}_i=0$ |
Par cons quent, en consid rant que le signe de chaque couple d pend de la direction dans laquelle il induit une rotation,
$d_1F_1-d_2F_2=0$
ce qui donne comme r sultat
.
(ID 3250)
(ID 4431)
(ID 4431)
Exemples
(ID 15845)
tant donn que le couple g n r par la force gravitationnelle et le bras de levier est
| $ T = r F $ |
de chaque c t de la balance, il doit s'annuler en cas d' quilibre pour atteindre l' quilibre :
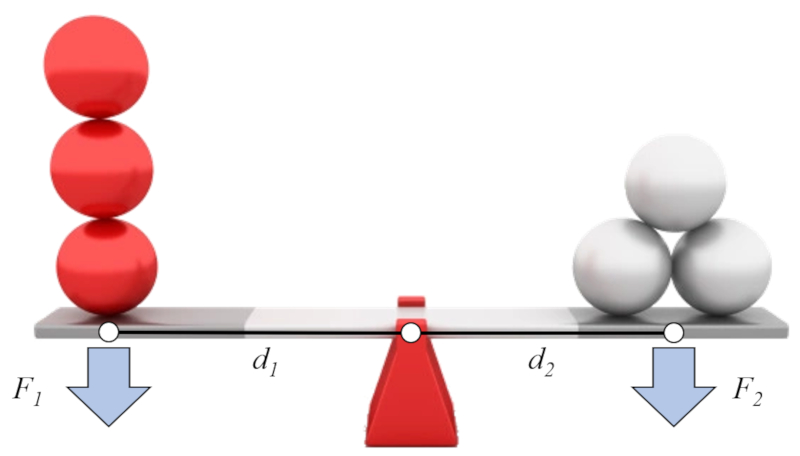
Si l'on suppose que d'un c t , nous avons a forcer 1 ($F_1$) et a force de distance - axe (bras) 1 ($d_1$), et de l'autre c t a forcer 2 ($F_2$) et a force de distance - axe (bras) 2 ($d_2$), on peut tablir la loi dite du levier comme suit :
| $ d_1 F_1 = d_2 F_2 $ |
(ID 15847)
(ID 15846)
Si une barre mont e sur un point servant d'axe est soumise a forcer 1 ($F_1$) A force de distance - axe (bras) 1 ($d_1$) de l'axe, g n rant un couple $T_1$, et a forcer 2 ($F_2$) A force de distance - axe (bras) 2 ($d_2$) de l'axe, g n rant un couple $T_2$, elle sera en quilibre si les deux couples sont gaux. Ainsi, l' quilibre correspond la loi du levier, exprim e comme suit :
| $ d_1 F_1 = d_2 F_2 $ |
(ID 3250)
Puisque la relation entre le moment angulaire et le moment est
| $ L = r p $ |
sa d riv e temporelle nous conduit la relation du moment de force
| $ T = r F $ |
La rotation du corps se produit autour d'un axe dans la direction du moment de force, qui passe par le centre de masse.
(ID 4431)
Puisque la relation entre le moment angulaire et le moment est
| $ L = r p $ |
sa d riv e temporelle nous conduit la relation du moment de force
| $ T = r F $ |
La rotation du corps se produit autour d'un axe dans la direction du moment de force, qui passe par le centre de masse.
(ID 4431)
A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.
Par cons quent, on en conclut que :
| $ F_g = m_g g $ |
(ID 3241)
A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.
Par cons quent, on en conclut que :
| $ F_g = m_g g $ |
(ID 3241)
ID:(1457, 0)