Mit konstanter Beschleunigung abfangen
Storyboard 
Objekte können sich kreuzen, wenn sie zum gleichen Zeitpunkt an derselben Position übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Ausgangspunkten und Geschwindigkeiten aus bewegen und Beschleunigungen erfahren, die es ihnen ermöglichen, am Ende der Reise in Position und Zeit übereinzustimmen.
ID:(1412, 0)
Mit konstanter Beschleunigung abfangen
Beschreibung 
Objekte können sich kreuzen, wenn sie zum gleichen Zeitpunkt an derselben Position übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Ausgangspunkten und Geschwindigkeiten aus bewegen und Beschleunigungen erfahren, die es ihnen ermöglichen, am Ende der Reise in Position und Zeit übereinzustimmen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
| $ a_0 = \bar{a} $ |
.
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
| $ dv \equiv v - v_0 $ |
und der Abgelaufene Zeit ($\Delta t$) als
| $ \Delta t \equiv t - t_0 $ |
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
| $ a_0 = \bar{a} $ |
.
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
| $ dv \equiv v - v_0 $ |
und der Abgelaufene Zeit ($\Delta t$) als
| $ \Delta t \equiv t - t_0 $ |
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
| $ \Delta s = s - s_0 $ |
Daraus folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
| $ \Delta s = s - s_0 $ |
Daraus folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
| $ v = v_0 + a_0 ( t - t_0 )$ |
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
| $ v = v_0 + a_0 ( t - t_0 )$ |
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
| $ dv \equiv v - v_0 $ |
und
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
innerhalb dieses Zeitintervalls definiert.
(ID 3678)
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
| $ dv \equiv v - v_0 $ |
und
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
innerhalb dieses Zeitintervalls definiert.
(ID 3678)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
(ID 4355)
(ID 4355)
Beispiele
(ID 15399)
In einem Szenario mit der Bewegung von zwei K rpern ndert der erste seine Geschwindigkeit um die Geschwindigkeitsunterschied des ersten Körpers ($\Delta v_1$) w hrend eine Reisezeit des ersten Objekts ($\Delta t_1$) mit die Erste Körperbeschleunigung ($a_1$).
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
Anschlie end bewegt sich der zweite K rper vorw rts und ndert seine Geschwindigkeit um die Geschwindigkeitsunterschied des zweiten Körpers ($\Delta v_2$) w hrend eines Zeitraums von die Reisezeit des zweiten Objekts ($\Delta t_2$) mit die Beschleunigung des zweiten Körpers ($a_2$).
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
Wenn dies grafisch dargestellt wird, erhalten wir ein Geschwindigkeits-Zeit-Diagramm wie unten gezeigt:
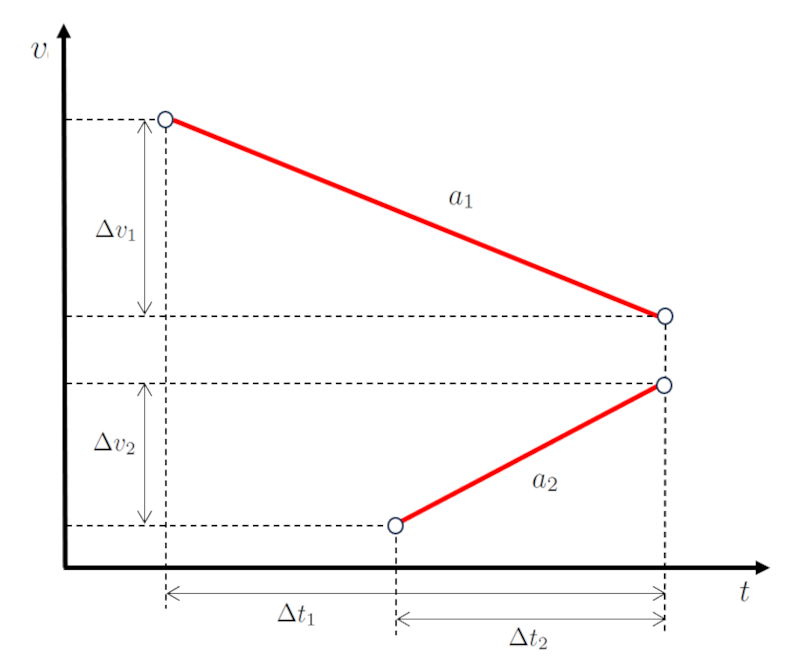
Der Schl ssel hierbei ist, dass die Werte die Geschwindigkeitsunterschied des ersten Körpers ($\Delta v_1$) und die Geschwindigkeitsunterschied des zweiten Körpers ($\Delta v_2$) sowie die Werte die Reisezeit des ersten Objekts ($\Delta t_1$) und die Reisezeit des zweiten Objekts ($\Delta t_2$) so gew hlt sind, dass sich beide K rper am gleichen Ort und zur gleichen Zeit treffen.
(ID 12512)
Im Falle von zwei K rpern kann die Bewegung des ersten durch eine Funktion beschrieben werden, die die Punkte der Anfangszeit des ersten Objekts ($t_1$), der Kreuzungszeit ($t$), die Anfangsgeschwindigkeit des ersten Körpers ($v_{01}$) und die Endgeschwindigkeit des ersten Körpers ($v_1$) involviert, dargestellt durch eine Gerade mit einer Steigung von die Erste Körperbeschleunigung ($a_1$):
| $ v_1 = v_{01} + a_1 ( t - t_1 )$ |
F r die Bewegung des zweiten K rpers, definiert durch die Punkte die Anfangsgeschwindigkeit des zweiten Körpers ($v_{02}$), die Endgeschwindigkeit des zweiten Körpers ($v_2$), der Anfangszeit des zweiten Objekts ($t_2$) und der Kreuzungszeit ($t$), wird eine zweite Gerade mit einer Steigung von die Beschleunigung des zweiten Körpers ($a_2$) verwendet:
| $ v_2 = v_{02} + a_2 ( t - t_2 )$ |
Dies wird wie folgt dargestellt:

(ID 12515)
Im Falle einer Bewegung von zwei K rpern stimmt die Position, an der die Bahn des ersten K rpers endet, mit der des zweiten K rpers bei die Kreuzungsposition ($s$) berein.
Ebenso stimmt die Zeit, zu der die Bahn des ersten K rpers endet, mit der des zweiten K rpers bei der Kreuzungszeit ($t$) berein.
F r den ersten K rper h ngt die Kreuzungsposition ($s$) von die Anfangsposition des ersten Objekts ($s_1$), die Anfangsgeschwindigkeit des ersten Körpers ($v_{01}$), die Erste Körperbeschleunigung ($a_1$), der Anfangszeit des ersten Objekts ($t_1$) ab, wie folgt:
| $ s = s_1 + v_{01} ( t - t_1 )+\displaystyle\frac{1}{2} a_1 ( t - t_1 )^2$ |
W hrend f r den zweiten K rper die Kreuzungsposition ($s$) von die Anfangsposition des zweiten Objekts ($s_2$), die Anfangsgeschwindigkeit des zweiten Körpers ($v_{02}$), die Beschleunigung des zweiten Körpers ($a_2$), der Anfangszeit des zweiten Objekts ($t_2$) abh ngt, wie folgt:
| $ s = s_2 + v_{02} ( t - t_2 )+\displaystyle\frac{1}{2} a_2 ( t - t_2 )^2$ |
Dies wird wie folgt dargestellt:
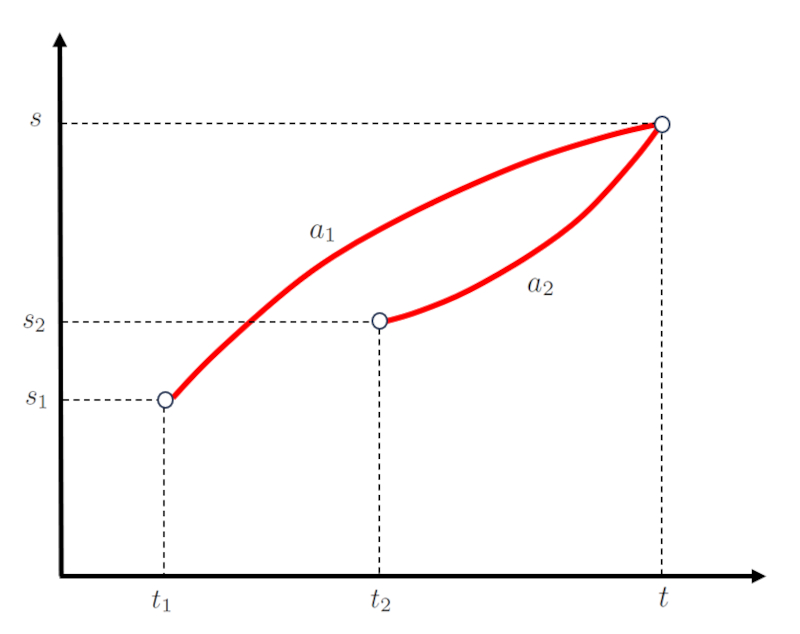
(ID 12513)
(ID 15402)
ID:(1412, 0)
