Benützer:
Hydraulische Elementnetzwerke
Storyboard
Wenn wir das Darcysche Gesetz mit dem Ohmschen Gesetz in der Elektrizität vergleichen, bemerken wir eine Analogie, bei der der Fluss der Flüssigkeit dem elektrischen Strom ähnelt, der Druckunterschied mit dem Spannungsunterschied zusammenhängt und die hydraulischen Elemente mit ihren hydraulischen Widerständen verglichen werden, ähnlich wie elektrische Widerstände.
Diese Analogie impliziert, dass neben elektrischen Netzwerken auch hydraulische Netzwerke definiert werden können, in denen die Gesamthydraulikwiderstände auf der Grundlage von Teilhydraulikwiderständen berechnet werden können.
ID:(1388, 0)
Hydrodynamische Netzwerke
Beschreibung
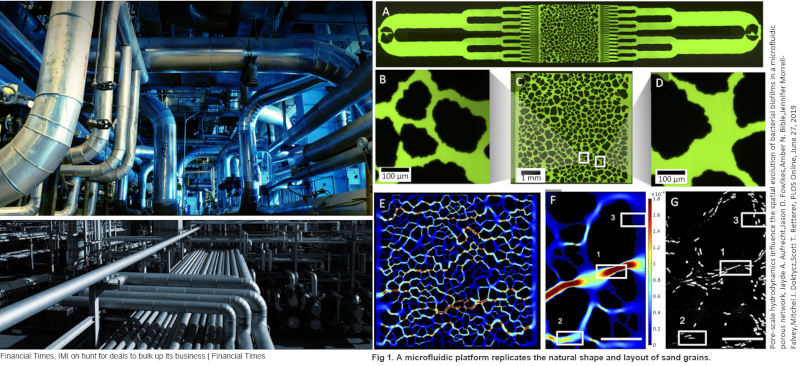
In der Natur gibt es mehrere Systeme, die als hydrodynamische Netzwerke dargestellt werden können, bei denen jedem Element ein hydraulischer Widerstand zugeordnet werden kann. Diese Systeme umfassen Netzwerke von Blutgefäßen in lebenden Organismen, Wasserleitungsnetze in Pflanzen oder Fluss- und Bachnetzwerke in Ökosystemen. Das Konzept des hydraulischen Widerstands ermöglicht es uns, zu verstehen, wie Flüssigkeiten in diesen Systemen fließen und sich verteilen, sowie deren Effizienz und Verhalten zu analysieren. Die Untersuchung von hydrodynamischen Netzwerken ist entscheidend, um natürliche Phänomene zu verstehen und effiziente künstliche Systeme zu entwerfen.
ID:(11098, 0)
Hydraulische Leitfähigkeit eines Rohres
Gleichung
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Zylinder Radio ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Zylinder Radio ($R$)) und der Art der Flüssigkeit (die Viskosität ($\eta$)) zusammenhängen. Diese Parameter können gemeinsam als eine Hydraulische Leitfähigkeit ($G_h$) bezeichnet werden:
 $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
ID:(15102, 0)
Darcys Gesetz und hydraulische Leitfähigkeit
Gleichung
Durch die Einführung von die Hydraulische Leitfähigkeit ($G_h$) können wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_h \Delta p $ |
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Zylinder Radio ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir die Hydraulische Leitfähigkeit ($G_h$) einführen, das in Bezug auf der Rohrlänge ($\Delta L$), der Zylinder Radio ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
ID:(14471, 0)
Hydraulische Leitfähigkeit
Gleichung
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitfähigkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) wäre, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_h = \displaystyle\frac{1}{G_h }$ |
ID:(15092, 0)
Hydraulischer Widerstand eines Rohres
Gleichung
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise können wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Zylinder Radio ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenhängen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden können:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Da die Hydraulic Resistance ($R_h$) gemäß der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
| $ R_h = \displaystyle\frac{1}{G_h }$ |
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Zylinder Radio ($R$) und der Rohrlänge ($\Delta L$) ausgedrückt wird:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
können wir folgern, dass:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
ID:(3629, 0)
Darcys Gesetz und hydraulischer Widerstand
Gleichung
Da der Volumenstrom ($J_V$) aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) mithilfe der folgenden Gleichung berechnet werden kann:
| $ J_V = G_h \Delta p $ |
kann es in Bezug auf die Druckunterschied ($\Delta p$) ausgedrückt werden. Wenn man berücksichtigt, dass das Inverse von die Hydraulic Resistance ($R_h$) Die Hydraulische Leitfähigkeit ($G_h$) ist, erhalten wir den folgenden Ausdruck:
| $ \Delta p = R_h J_V $ |
Im Fall eines einzelnen Zylinders die Hydraulic Resistance ($R_h$), der von die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und der Zylinder Radio ($R$) abhängt, wird er mithilfe der folgenden Gleichung berechnet:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Das Hagen-Poiseuille-Gesetz hingegen ermöglicht die Berechnung von der Volumenstrom ($J_V$), das von die Druckunterschied ($\Delta p$) gemäß der folgenden Gleichung erzeugt wird:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Durch Kombination beider Gleichungen erhalten wir das Darcy-Gesetz:
| $ \Delta p = R_h J_V $ |
den Henry Darcy formuliert hat, um das allgemeine Verhalten von komplexeren porösen Medien zu modellieren, durch die eine Flüssigkeit fließt.
Die Genialität dieser Art der Umformulierung des Hagen-Poiseuille-Gesetzes liegt darin, dass sie die Analogie zwischen dem Fluss von elektrischem Strom und dem Fluss von Flüssigkeit zeigt. In diesem Sinne entspricht das Hagen-Poiseuille-Gesetz dem Ohm'schen Gesetz. Dies eröffnet die Möglichkeit, die Konzepte elektrischer Netzwerke auf Systeme von Rohren anzuwenden, durch die eine Flüssigkeit fließt.
Dieses Gesetz, auch als das Darcy-Weisbach-Gesetz bekannt, wurde erstmals in Darcys Werk veröffentlicht:
• "Les fontaines publiques de la ville de Dijon" ("Die öffentlichen Brunnen der Stadt Dijon"), Henry Darcy, Victor Dalmont Editeur, Paris (1856).
ID:(3179, 0)
Summe der parallelen Flüsse
Gleichung
Die Summe der Bodenschichten in Parallele, dargestellt als der Gesamtfluss ($J_{Vt}$), entspricht der Summe von der Volumenstrom in einem Netzwerk ($J_{Vk}$):
| $ J_{Vt} =\displaystyle\sum_k J_{Vk} $ |
.
ID:(4376, 0)
Summe der Seriendrücke
Gleichung
Die Gesamtdruckdifferenz ($\Delta p_t$) em relação às diferentes Druckunterschied in einem Netzwerk ($\Delta p_k$), o que nos leva à seguinte conclusão:
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
ID:(4377, 0)