Buoyancy
Storyboard 
When an object is submerged in a liquid medium, it experiences the pressure of that medium. Because pressure increases with depth, it is greater on the lower part of the object than on the upper part, creating a force upward toward the surface, known as buoyant force. If this force exceeds the object's gravity, it will rise to the surface and float. If it is less, it will slow down the rate of sinking but will continue to descend until it reaches the bottom.
ID:(1609, 0)
Buoyancy
Storyboard 
When an object is submerged in a liquid medium, it experiences the pressure of that medium. Because pressure increases with depth, it is greater on the lower part of the object than on the upper part, creating a force upward toward the surface, known as buoyant force. If this force exceeds the object's gravity, it will rise to the surface and float. If it is less, it will slow down the rate of sinking but will continue to descend until it reaches the bottom.
Variables
Calculations
Calculations
Equations
Pressure is defined as:
The pressure difference is:
The section multiplied by the height of the body is equal to its volume:
Therefore, the buoyant force on a submerged body is:
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
That is:
The buoyancy force ($F_b$) is determined by the liquid density ($\rho_w$), the displaced volume ($V_b$), and the gravitational Acceleration ($g$) as:
which opposes the gravitational Force ($F_g$) with the mass of floating object ($M_s$) according to:
therefore, with the mass of the displaced liquid ($M_b$) and the mass of floating object ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
it follows that
Given that with the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$),
relates to the object Density ($\rho_s$) and the object volume ($V_s$) by
while it holds true that with the liquid density ($\rho_w$) and the ballast volume ($V_w$) we have
we obtain the relationship
Since the displaced volume ($V_b$) is the submerged volume ($V_s$), but including the ballast volume ($V_w$), we have
and the equation for the liquid density ($\rho_w$) represented by
we can calculate the mass of the displaced liquid ($M_b$) as
The buoyancy force ($F_b$) is determined by the liquid density ($\rho_w$), the displaced volume ($V_b$), and the gravitational Acceleration ($g$) as:
which opposes the gravitational Force ($F_g$) with the mass of floating object ($M_s$) as:
If both forces are equal:
the object will float.
Examples
When an object hanging from a dynamometer is submerged in a liquid, it is observed that the force indicated by it decreases, indicating the existence of a buoyant force a buoyancy force ($F_b$) generated by the liquid.
When an object floats, the buoyant force the buoyancy force ($F_b$) must be equal to the gravitational Force ($F_g$), explaining why it neither sinks nor emerges.
To explain the lift experienced by a submerged body, it is necessary to study the vertical pressures to which it is exposed. Since the bottom face of the body is at a greater depth than the top face, the pressure at the bottom is greater than at the top, resulting in a net upward force that generates the observed lift. This phenomenon is similar when a body floats on the surface, where there is no water pressure on it; again, it is the pressure at the bottom that generates lift.
Therefore, in the case where the body is submerged, we obtain:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
Or similarly on the surface:
Finally, the lift force is obtained using the definition of pressure, which for the pressure at the base ($\Delta p$) with the buoyancy force ($F_b$) and the floating body section ($S_s$) corresponds to:
A body floats if the buoyant force the buoyancy force ($F_b$) equals the weight of the body the gravitational Force ($F_g$):
This implies that the relationship between the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$) establishes:
Which corresponds to the principle of Archimedes [1].
which states:
Any floating object displaces its own weight in liquid.
![]() [1] "Peri ton eightumenon" (On floating bodies), Archimedes, 287 to 212 BC.
[1] "Peri ton eightumenon" (On floating bodies), Archimedes, 287 to 212 BC.
Given that with the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$),
relates to the object Density ($\rho_s$) and the object volume ($V_s$) by
while it holds true that with the liquid density ($\rho_w$) and the ballast volume ($V_w$) we have
we obtain the relationship
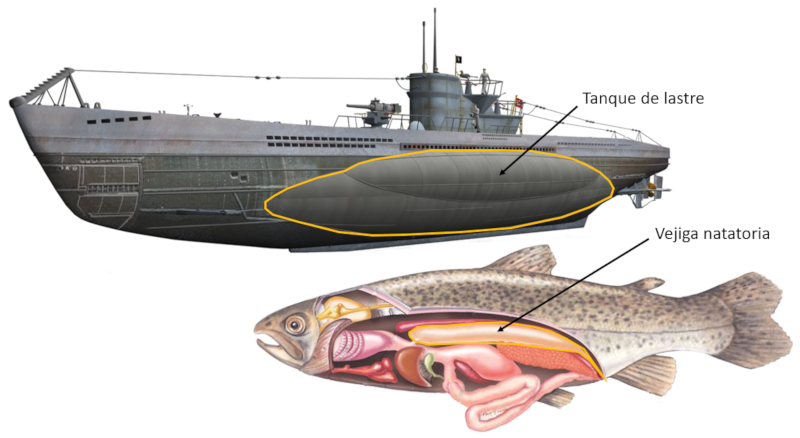
Therefore, an object with a higher density than water can float as long as it has a low volume of air below the waterline (surface of the water). In the case of a boat, this is the space occupied by cargo and/or passengers, while in a submarine, it is the ballast tanks, and in a fish, it is the swim bladder.
It is important to note that:
For a submerged object, suspension, ascent, or descent does not depend on the depth at which it is located. However, the ability to pump air into the ballast tank or swim bladder does depend on the surrounding pressure.
The density of water is not homogeneous in the sea, which means that a submerged object has to adjust the volume of air used in the ballast tank or swim bladder as it moves.
Submarines and fish have the ability to adjust the depth at which they remain in the water. They can ascend to the surface (float) or descend, limited only by the pressure they can withstand. They achieve this by using ballast tanks (in submarines) and swim bladders (in fish), which are spaces where air can expand, occupying a greater volume of displaced water.
To achieve this, the equality between the mass of the displaced liquid ($M_b$) and the mass of floating object ($M_s$) can be rewritten in terms of the liquid density ($\rho_w$), the object Density ($\rho_s$), and the object volume ($V_s$), allowing for the adjustment of the ballast volume ($V_w$):
allowing one to be equal to or exceed the other. In summary, if the ballast volume ($V_w$) is increased, buoyancy increases, causing ascent; reducing the volume results in descent. If the volume remains the same, they remain suspended.
An interesting study on how whales use the Spermaceti organ to control buoyancy through heat and fats can be read in the study Buoyancy Control as a Function of the Spermaceti Organ in the Sperm Whale by Malcolm R. Clarke, published in J.mar.bio.Ass U.K. (1978) 58, 27-71.
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
The the pressure at the base ($\Delta p$) that exists in the deepest plane of the body is with the object draft ($d$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) then:
The buoyancy force ($F_b$) can be expressed in terms of the displaced volume ($V_b$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) with:
Note: The volume considered here is the submerged volume. If the body is not fully submerged, only the volume corresponding to the displaced liquid should be considered.
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
If the gravitational Force ($F_g$) is equal to the buoyancy force ($F_b$):
the object will float.
If the buoyancy force ($F_b$) and the gravitational Force ($F_g$) are equal, the object will float. In this case, it means that the mass of floating object ($M_s$) must be equal to the mass of the displaced liquid ($M_b$), resulting in:
Note: this relationship is only possible if the object 'weighs less than water', which means the displaced water occupies an equal or greater volume than the object.
When a body is submerged, the ballast volume ($V_w$) in ballast tank is included with the object volume ($V_s$) in the displaced volume ($V_b$) total. Therefore, we have:
With the volume of displaced water equal to the sum of the ballast volume ($V_w$) and the submerged volume ($V_s$), which can be calculated with the liquid density ($\rho_w$), the mass of the displaced liquid ($M_b$) can be determined:
The float condition is with the ballast volume ($V_w$), the liquid density ($\rho_w$), the object Density ($\rho_s$) and the object volume ($V_s$):
ID:(1609, 0)