Flottation
Storyboard 
Quand un objet est immergé dans un milieu liquide, il subit la pression de ce milieu. Comme la pression augmente avec la profondeur, elle est plus grande sur la partie inférieure de l'objet que sur la partie supérieure, créant une force dirigée vers le haut en direction de la surface, appelée force de flottabilité. Si cette force est supérieure à la gravité de l'objet, celui-ci remontera à la surface et flottera. Si elle est inférieure, elle ralentira la vitesse de descente mais continuera à descendre jusqu'à toucher le fond.
ID:(1609, 0)
Flottation
Storyboard 
Quand un objet est immergé dans un milieu liquide, il subit la pression de ce milieu. Comme la pression augmente avec la profondeur, elle est plus grande sur la partie inférieure de l'objet que sur la partie supérieure, créant une force dirigée vers le haut en direction de la surface, appelée force de flottabilité. Si cette force est supérieure à la gravité de l'objet, celui-ci remontera à la surface et flottera. Si elle est inférieure, elle ralentira la vitesse de descente mais continuera à descendre jusqu'à toucher le fond.
Variables
Calculs
Calculs
Équations
La pression est d finie comme :
La diff rence de pression est :
La section transversale du corps multipli e par sa hauteur correspond son volume :
Ainsi, la force de flottaison sur un corps immerg est :
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
C'est- -dire :
A force de poussée ($F_b$) est d termin par a densité du liquide ($\rho_w$), le volume déplacé ($V_b$) et a accélération gravitationnelle ($g$) comme :
ce qui s'oppose a force gravitationnelle ($F_g$) avec a masse d'un objet flottant ($M_s$) selon :
donc, avec ERROR:8663 et a masse d'un objet flottant ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
nous avons :
tant donn que avec a masse d'un objet flottant ($M_s$) et ERROR:8663,
se rapporte a densité des objets ($\rho_s$) et le volume de l'objet ($V_s$) par
tandis qu'avec a densité du liquide ($\rho_w$) et le volume de ballast ($V_w$) nous avons
nous obtenons la relation
Puisque le volume déplacé ($V_b$) est le volume immergé ($V_s$), mais en incluant le volume de ballast ($V_w$), nous avons
et l' quation pour a densité du liquide ($\rho_w$) repr sent e par
nous pouvons calculer ERROR:8663 comme
A force de poussée ($F_b$) est d termin par a densité du liquide ($\rho_w$), le volume déplacé ($V_b$) et a accélération gravitationnelle ($g$) comme :
ce qui s'oppose a force gravitationnelle ($F_g$) avec a masse d'un objet flottant ($M_s$) comme :
Si les deux forces sont gales :
l'objet flottera.
Exemples
Lorsqu'un objet suspendu un dynamom tre est immerg dans un liquide, on observe que la force indiqu e par celui-ci diminue, ce qui indique l'existence d'une force de pouss e une force de poussée ($F_b$) g n r e par le liquide.
Lorsqu'un objet flotte, la force de pouss e a force de poussée ($F_b$) doit tre gale a a force gravitationnelle ($F_g$), expliquant pourquoi il ne coule ni n' merge.
Pour expliquer la portance subie par un corps immerg , il faut tudier les pressions verticales auxquelles il est expos . tant donn que la face inf rieure du corps est plus profonde que la face sup rieure, la pression en bas est plus grande qu'en haut, ce qui entra ne une force ascendante nette qui g n re la portance observ e. Ce ph nom ne est similaire lorsqu'un corps flotte la surface, o il n'y a aucune pression d'eau sur lui ; encore une fois, c'est la pression au fond qui g n re la portance.
Ainsi, dans le cas o le corps est immerg , on obtient :
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
Ou de mani re similaire en surfacexa0:
Enfin, la force de portance est obtenue l'aide de la d finition de la pression, qui pour a pression à la base ($\Delta p$) avec a force de poussée ($F_b$) et a section du corps flottant ($S_s$) correspond xa0:
Un corps flotte si la force de pouss e a force de poussée ($F_b$) est gale au poids du corps a force gravitationnelle ($F_g$) :
Cela implique que la relation entre a masse d'un objet flottant ($M_s$) et ERROR:8663 tablit :
Ce qui correspond au principe d'Archim de [1].
qui affirme :
Tout objet flottant d place son propre poids en liquide.
![]() [1] "Peri ton Eightumenon" (Sur les corps flottants), Archim de, 287 212 av.
[1] "Peri ton Eightumenon" (Sur les corps flottants), Archim de, 287 212 av.
tant donn que avec a masse d'un objet flottant ($M_s$) et ERROR:8663,
se rapporte a densité des objets ($\rho_s$) et le volume de l'objet ($V_s$) par
tandis qu'avec a densité du liquide ($\rho_w$) et le volume de ballast ($V_w$) nous avons
nous obtenons la relation
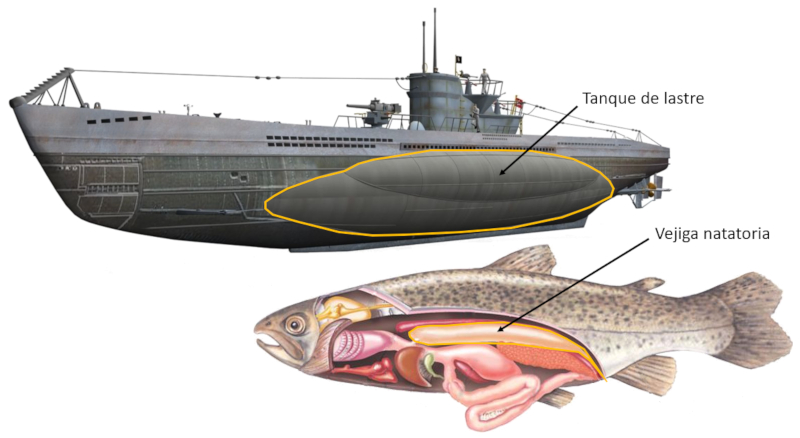
Ainsi, un objet avec une densit sup rieure celle de l'eau peut flotter tant qu'il a un faible volume d\'air en dessous de la ligne de flottaison (surface de l\'eau). Dans le cas d\'un bateau, il s\'agit de l\'espace occup par la cargaison et/ou les passagers, tandis que dans un sous-marin, il s\'agit des r servoirs de ballast, et dans un poisson, il s\'agit de la vessie natatoire.
Il est important de noter que :
Pour un objet submerg , la suspension, l\'ascension ou la descente ne d pendent pas de la profondeur laquelle il se trouve. Cependant, la capacit de pomper de l\'air dans le r servoir de ballast ou la vessie natatoire d pend de la pression environnante.
La densit de l\'eau n\'est pas homog ne dans la mer, ce qui signifie qu\'un objet submerg doit ajuster le volume d\'air utilis dans le r servoir de ballast ou la vessie natatoire mesure qu\'il se d place.
Les sous-marins et les poissons ont la capacit d'ajuster la profondeur laquelle ils se maintiennent dans l'eau. Ils peuvent remonter la surface (flotter) ou descendre, limit s seulement par la pression qu'ils peuvent supporter. Cela est r alis gr ce l'utilisation de ballasts (dans les sous-marins) et de vessies natatoires (chez les poissons), qui sont des espaces o l'air peut se dilater, occupant ainsi un volume plus important d'eau d plac e.
Pour y parvenir, l' galit entre ERROR:8663 et a masse d'un objet flottant ($M_s$) peut tre r crite en fonction de a densité du liquide ($\rho_w$), a densité des objets ($\rho_s$) et le volume de l'objet ($V_s$), permettant l'ajustement de le volume de ballast ($V_w$) :
permettant l'une d' tre gale ou de d passer l'autre. En r sum , si le volume de ballast ($V_w$) est augment , la flottabilit augmente, provoquant une ascension ; en r duisant le volume, l'objet descend. Si le volume reste le m me, ils restent en suspension.
Um estudo interessante sobre como as baleias usam o rg o de espermacete para controlar a flutuabilidade atrav s de calor e gorduras pode ser encontrado no estudo "Buoyancy Control as a Function of the Spermaceti Organ in the Sperm Whale" de Malcolm R. Clarke, publicado em J.mar.bio.Ass U.K. (1978) 58, 27-71.
A pression de la colonne d'eau ($p$) se calcule partir de a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) comme suit :
Le a pression à la base ($\Delta p$) qui existe dans le plan le plus profond du corps est avec le brouillon d'objet ($d$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) alors :
A force de poussée ($F_b$) peut tre exprim en termes de le volume déplacé ($V_b$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) avec :
Remarque : Le volume consid r ici est le volume immerg . Si le corps n'est pas enti rement immerg , seul le volume correspondant au liquide d plac doit tre pris en compte.
A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.
Par cons quent, on en conclut que :
Si a force gravitationnelle ($F_g$) est gal a force de poussée ($F_b$) :
l'objet flottera.
Si a force de poussée ($F_b$) et a force gravitationnelle ($F_g$) sont gaux, l'objet flottera. Dans ce cas, cela signifie que a masse d'un objet flottant ($M_s$) doit tre gal ERROR:8663, ce qui donne :
Note : cette relation n'est possible que si l'objet 'p se moins que l'eau', ce qui signifie que l'eau d plac e occupe un volume gal ou sup rieur celui de l'objet.
Lorsqu'un corps est submerg , le volume de ballast ($V_w$) dans le ballast est inclus avec le volume de l'objet ($V_s$) dans un total de le volume déplacé ($V_b$). Par cons quent, nous avons :
Avec le volume d'eau d plac e gal la somme de le volume de ballast ($V_w$) et le volume immergé ($V_s$), qui peut tre calcul avec a densité du liquide ($\rho_w$), nous pouvons d terminer ERROR:8663 :
La condition float est avec le volume de ballast ($V_w$), a densité du liquide ($\rho_w$), a densité des objets ($\rho_s$) et le volume de l'objet ($V_s$)xa0:
ID:(1609, 0)