Utilizador:
Estabilidade de flutuabilidade
Storyboard 
A força gerada pela flutuação atua no centro do volume deslocado, que geralmente está abaixo do centro de massa do objeto na água. Essa dupla de forças resulta em torques que podem estabilizar ou desestabilizar o objeto. No segundo caso, ele pode até mesmo virar. Esse princípio se aplica tanto a objetos inanimados quanto a organismos vivos, que, devido a doenças, podem ter dificuldade em manter uma posição vertical.
ID:(1610, 0)
Mecanismos
Iframe
Mecanismos
ID:(15481, 0)
O desastre de Vasa
Descrição
O navio de guerra sueco Vasa é um exemplo conhecido de um navio instável. Em 10 de agosto de 1628, apenas 20 minutos após deixar o estaleiro em sua viagem inaugural no porto de Estocolmo, o navio virou e afundou:
O projeto do navio era falho, pois sua construção estreita pretendia atingir altas velocidades e sua estrutura alta pretendia acomodar 64 canhões, um número significativo. No entanto, esse projeto tornou o navio intrinsecamente instável, levando ao seu viramento com a primeira rajada de vento.
Felizmente, o navio afundou em águas rasas e foi preservado na água salgada por 333 anos até sua recuperação em 1961. Inicialmente, o navio foi mantido molhado e depois lentamente substituíram a água por uma mistura de cera que permitiu exibi-lo completamente seco em um museu a poucos metros de onde ele afundou.
O Vasa serve como um lembrete na construção naval, demonstrando a importância de um design cuidadoso e estabilidade. Sua exibição no museu é uma atração popular, atraindo visitantes de todo o mundo para ver esta notável peça da história marítima.
ID:(11977, 0)
Ponto flutuante de ataque
Descrição
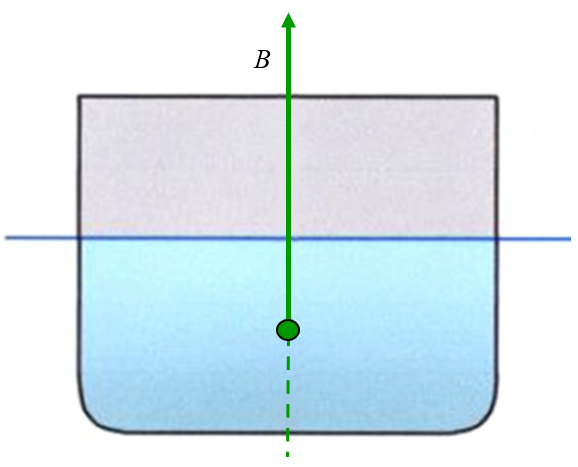
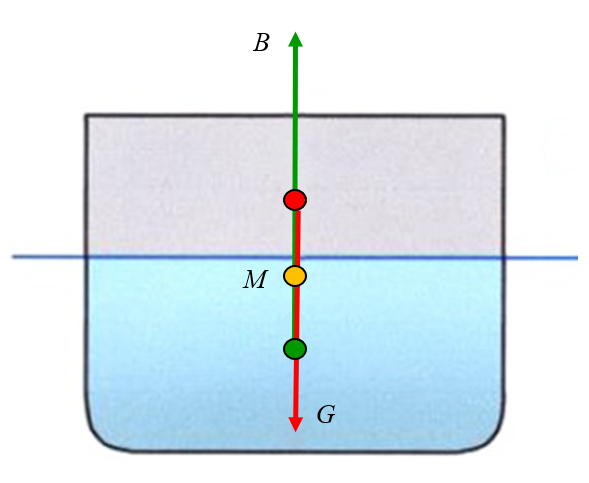
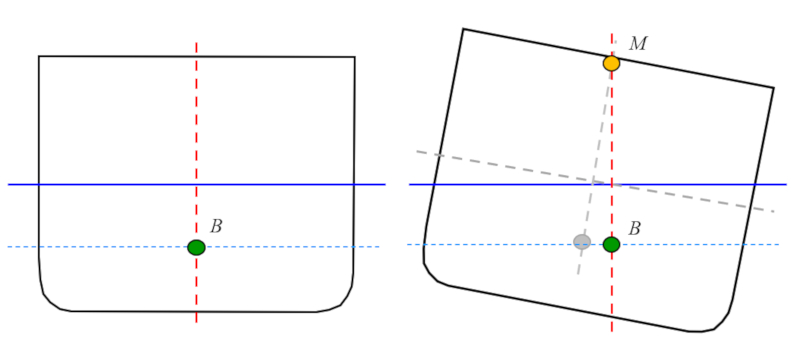
O ponto de aplicação da força de empuxo é igual ao centro de massa do volume de líquido deslocado:
Em um barco típico com perfil quadrado, isso corresponde a um ponto localizado na metade do calado (profundidade de submersão).
ID:(11957, 0)
Defina o metacentro
Descrição
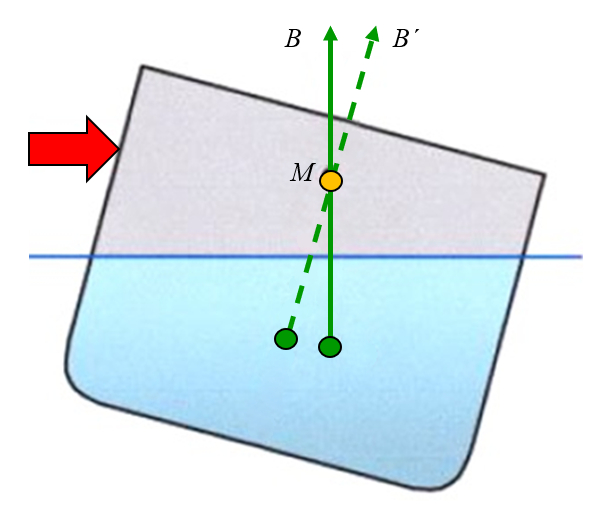
Se uma força lateral é aplicada e o objeto é inclinado, pode-se observar que o ponto em que a força de empuxo atua se desloca para fora do eixo. Desenhando uma linha vertical a partir dessa nova posição, resulta em que a linha cruza o eixo central em um ponto conhecido como metacentro:
ID:(11959, 0)
Ação da gravidade
Conceito
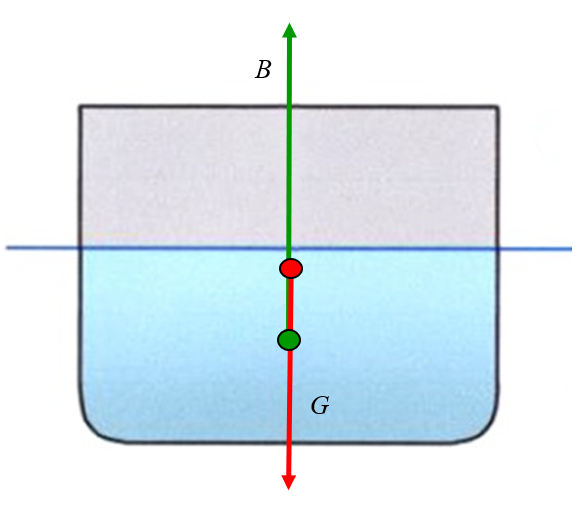
A gravidade atua sobre o centro de massa, que geralmente está localizado acima do ponto de aplicação da força de empuxo, mas pode estar acima ou abaixo do metacentro:
ID:(11960, 0)
Situação estável
Descrição
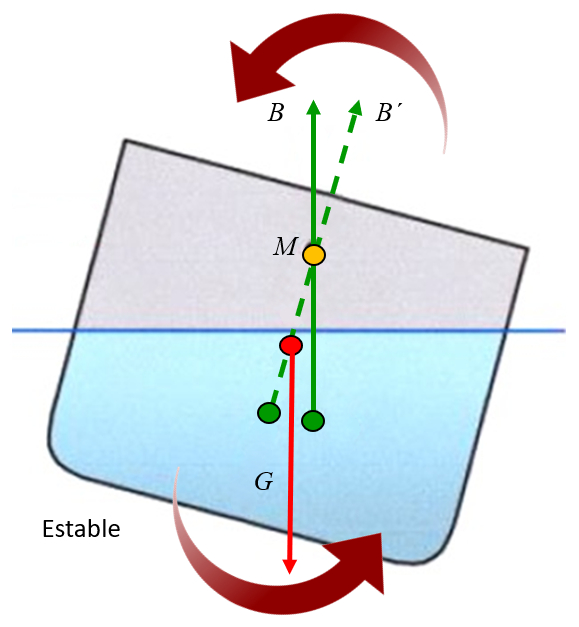
Se o metacentro estiver acima do centro de massa, a força da gravidade gera um torque que tende a estabilizar o objeto. É como se o objeto estivesse suspenso no metacentro e a força da gravidade gerasse rotações em torno dele. Quando o centro de massa está abaixo do metacentro, o torque gera uma rotação em direção ao eixo, ou seja, tende a corrigir o tombamento, estabilizando assim o objeto:
ID:(11961, 0)
Metacentro abaixo do centro de gravidade
Descrição
Se o metacentro estiver acima ou abaixo do centro de gravidade, isso pode facilmente ocorrer se uma carga for adicionada à parte superior, fazendo com que o centro de massa suba, o que leva ao sistema se tornar instável.
Nota: para evitar a perda de estabilidade, é importante posicionar a carga em uma posição baixa (fundo do barco).
ID:(11962, 0)
Situação instável
Descrição
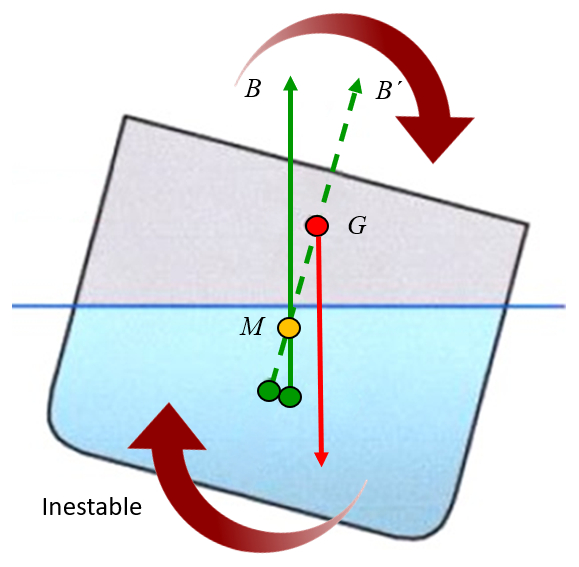
Se o metacentro estiver abaixo do centro de massa, a força da gravidade gera um torque que tende a desestabilizar o objeto. É como se o objeto estivesse suspenso no metacentro e a força da gravidade gerasse rotações em torno dele. Quando o centro de massa está acima do metacentro, o torque gera uma rotação afastando-o do eixo, ou seja, tende a aumentar a inclinação e, portanto, a desestabilizar o objeto:
ID:(11963, 0)
Modelo do casco de um navio
Descrição
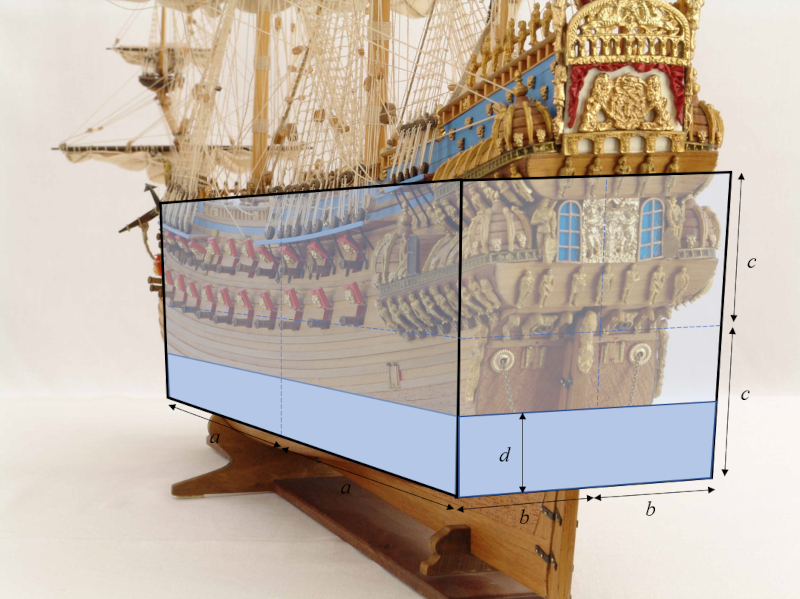
O modelo do casco do navio é reduzido a um paralelepípedo com comprimentos de o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e la meia altura do paralelepípedo ($c$), resultando em dimensões de $2a \times 2b \times 2c$, com um calado de um rascunho de objeto ($d$):
ID:(11969, 0)
Modelo simplificado: paralelepípedo reto
Conceito
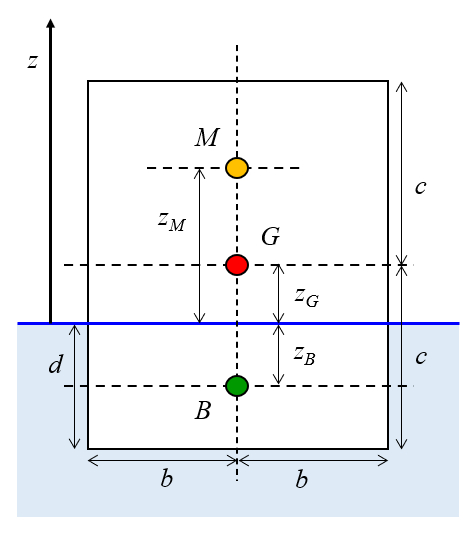
Um modelo comumente utilizado para barcos é o de um paralelepípedo reto com comprimentos de o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e la meia altura do paralelepípedo ($c$), e um centro de massa em seu centro geométrico. Quando colocado na água, o corpo afunda até uma profundidade de um rascunho de objeto ($d$). A posição do centro onde a força de flutuação atua pode ser vista na seguinte imagem, com coordenadas la ponto de altura da força de empuxo de ataque ($z_B$), la altura do centro de massa ($z_G$) e la altura do metacentro ($z_M$):
Portanto la altura do centro de massa ($z_G$) é
| $ z_G = c - d $ |
ID:(11964, 0)
Definindo a posição do metacentro
Descrição
O metacentro é calculado determinando o centro de massa do corpo inclinado sob a condição de que a área abaixo da linha de flutuação (linha azul) seja constante:
ID:(11979, 0)
Cálculo da posição do centro de massa da água deslocada
Descrição
Quando o barco está adernado, uma seção maior de água se move de um lado e a mesma seção menor do lado oposto. O centro de massa é, portanto, deslocado do centro para o setor com maior deslocamento, que é calculado por
$\bar{x} = \displaystyle\frac{\displaystyle\sum_i m_i x_i}{\displaystyle\sum_i m_i}$
A massa é proporcional à seção calculada a partir de o meia largura do paralelepípedo ($b$) e o rascunho de objeto ($d$) por:
$2b d$
Todas as massas deslocadas em ambos os lados do eixo não contribuem para o numerador e apenas os dois triângulos indicados a partir de uma área com o ângulo do calcanhar ($\phi$)
$b^2\phi$
pesar a posição do centro de massa dos triângulos
$\displaystyle\frac{2b}{3}$
o que é visto no gráfico:
Portanto, a distância do centro de massa da água deslocada do eixo é
$\displaystyle\frac{\displaystyle\frac{2b}{3} b^2\phi}{2bd}=\displaystyle\frac{b^2\phi}{3d}$
ID:(14248, 0)
Cálculo da posição do metacentro
Descrição
Se um navio adernar em o ângulo do calcanhar ($\phi$), o centro de massa da água deslocada se move com o meia largura do paralelepípedo ($b$) e o metade do comprimento do paralelepípedo ($a$) a uma distância de:
$\displaystyle\frac{b^2\phi}{3d}$
Como esta distância é o arco do círculo que pode ser traçado em torno do metacentro, a distância entre o metacentro e o centro de massa da água deslocada, que corresponde ao raio, é:
$\displaystyle\frac{b^2}{3d}$
Portanto, a posição do metacentro deve levar em conta que o centro de coordenadas está na altura da superfície da água, que está a uma distância $d/2$ acima do centro de massa da água deslocada:
com la altura do metacentro ($z_M$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11967, 0)
Análise da condição de estabilidade para o paralelepípedo
Descrição
Para que o paralelepípedo seja estável, la altura do metacentro ($z_M$) deve sempre ser maior ou igual a la altura do centro de massa ($z_G$), ou seja,
| $ z_M \geq z_G $ |
Portanto, com la altura do centro de massa ($z_G$) sendo o ponto de aplicação da força de flutuação fornecida com la meia altura do paralelepípedo ($c$) e o rascunho de objeto ($d$):
| $ z_G = c - d $ |
e la altura do metacentro ($z_M$) sendo com o meia largura do paralelepípedo ($b$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
obtemos la condição de estabilidade de um corpo flutuante ($e$):
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
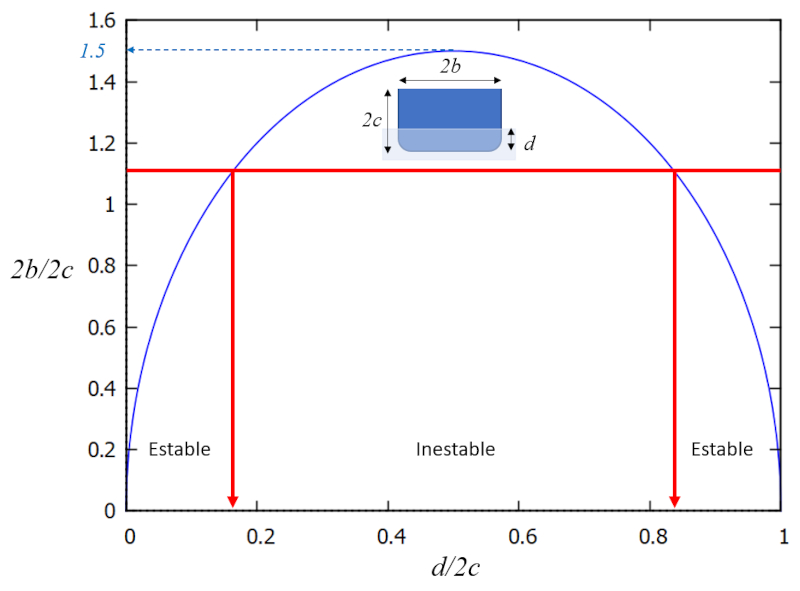
o que significa que existe uma região no gráfico $b/c$ (largura/profundidade) versus $d/2c$ (profundidade/altura) em que o sistema é estável, e em seu complemento, instável:
Ou seja, a estabilidade é alcançada com grandes valores de $b/c$ (largura maior que calado). No caso do navio Vasa, o problema era que o navio era alto demais para sua largura. Uma solução teria sido afundar mais ou alcançar um valor $d/c$ mais elevado para evitar a zona de instabilidade. Porém, isso não foi possível devido às aberturas dos canhões por onde teria entrado água.
Para obter mais informações sobre erros de compilação, consulte Por que o Vasa afundou: 10 problemas e alguns antídotos para projetos de software, Richard E. Fairley, Mary Jane Willshire, março/abril de 2003 IEEE SOFTWARE, que se aplica a projetos de software.
ID:(11976, 0)
Análise do caso Wasa
Descrição
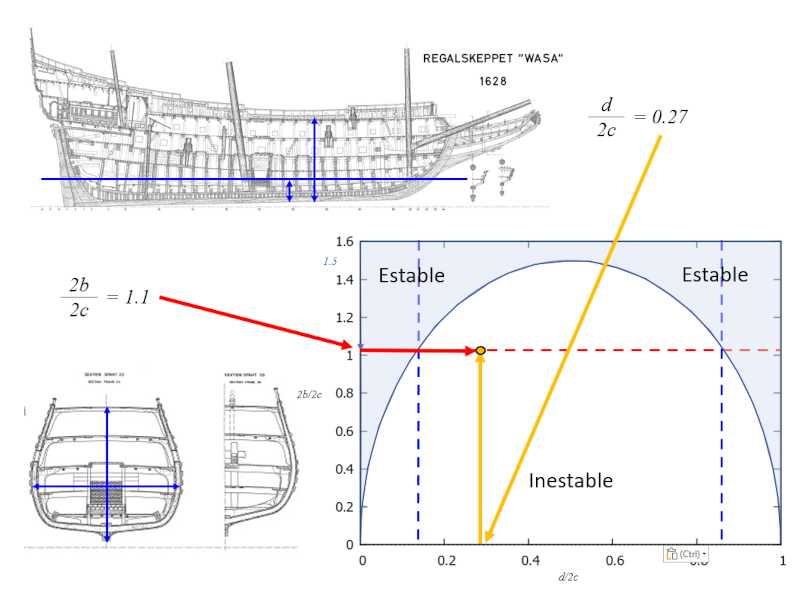
Ao estudar os planos da Vasa, é possível estimar os coeficientes da relação entre a largura e altura, bem como entre o calado e a altura. A partir disso, é possível mostrar que o navio é instável:
ID:(14247, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$
e = b ^2/(6* c ^2) - d *(1 - d /(2* c ))/(2* c )
$ M_b = M_s $
M_b = M_s
$ M_b =4 a b d \rho_w $
M_b =4* a * b * d * rho_w
$ M_s =8 a b c \rho_s $
M_s =8* a * b * c * rho_s
$ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$
rho_s / rho_w = d /(2* c )
$ V_b = 4 a b d $
V_b = 4 * a * b * d
$ z_B =-\displaystyle\frac{ d }{2}$
z_B =- d /2
$ z_G = c - d $
z_G = c - d
$ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$
z_M =- d /2 + b ^2/(3* d )
$ z_M \geq z_G $
z_M >= z_G
ID:(15483, 0)
Flotação, dependendo da massa
Equação
Se la força de empuxo ($F_b$) e la força gravitacional ($F_g$) forem iguais, o objeto flutuará. Neste caso, isso significa que la massa de objeto flutuante ($M_s$) deve ser igual a ($$), resultando em:
| $ M_b = M_s $ |
La força de empuxo ($F_b$) é determinada por la densidade líquida ($\rho_w$), o volume deslocado ($V_b$) e la aceleração gravitacional ($g$) como:
| $ F_b = \rho_w V_b g $ |
o que se opõe a la força gravitacional ($F_g$) com la massa de objeto flutuante ($M_s$) segundo:
| $ F_g = m_g g $ |
portanto, com ($$) e la massa de objeto flutuante ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
temos:
| $ M_b = M_s $ |
Nota: esta relação só é possível se o objeto 'pesar menos que a água', o que significa que a água deslocada ocupa um volume igual ou maior que o do objeto.
ID:(11955, 0)
Massa do objeto
Equação
La massa de objeto flutuante ($M_s$) pode ser calculado a partir de la densidade do objeto ($\rho_s$) e do volume dado pelos seus parâmetros geométricos o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e la meia altura do paralelepípedo ($c$).
Portanto:
| $ M_s =8 a b c \rho_s $ |
ID:(11970, 0)
Massa de água deslocada por modelo de navio
Equação
($$) pode ser calculado a partir de la densidade líquida ($\rho_w$) e do volume dado pelos seus parâmetros geométricos o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e o rascunho de objeto ($d$).
Portanto:
| $ M_b =4 a b d \rho_w $ |
ID:(11971, 0)
Volume deslocado
Equação
O volume deslocado ($V_b$) pode ser calculado a partir de seus parâmetros geométricos o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e o rascunho de objeto ($d$).
Portanto:
| $ V_b = 4 a b d $ |
ID:(11968, 0)
Princípio de Arquimedes para o paralelepípedo
Equação
O princípio de Arquimedes afirma que a massa da água deslocada é igual à massa do objeto. Para o caso específico do paralelepípedo reto, isso pode ser expresso como la densidade do objeto ($\rho_s$), la densidade líquida ($\rho_w$), o rascunho de objeto ($d$) e la meia altura do paralelepípedo ($c$) da seguinte forma:
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
Uma vez que o princípio de Arquimedes estabelece que ($$) é igual a la massa de objeto flutuante ($M_s$),
| $ M_b = M_s $ |
temos que ($$) está relacionado com la densidade líquida ($\rho_w$), o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e o rascunho de objeto ($d$) da seguinte forma:
| $ M_b =4 a b d \rho_w $ |
e la massa de objeto flutuante ($M_s$) está relacionado com la densidade do objeto ($\rho_s$), o metade do comprimento do paralelepípedo ($a$), o meia largura do paralelepípedo ($b$) e la meia altura do paralelepípedo ($c$) da seguinte maneira:
| $ M_s =8 a b c \rho_s $ |
o que implica que
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
ID:(11972, 0)
Posição do ponto de ataque do empuxo
Equação
O ponto em que atua a força de empuxo está localizado no centro de massa do volume de água deslocado pelo barco. No caso de o barco não estar inclinado (escorado), este ponto está localizado no centro do volume a meia altura do calado.
Levando isso em consideração, você pode expressar la ponto de altura da força de empuxo de ataque ($z_B$) como uma função de o rascunho de objeto ($d$) como:
| $ z_B =-\displaystyle\frac{ d }{2}$ |
ID:(11965, 0)
Posição do ponto de ataque da força gravitacional
Equação
O ponto de aplicação da força gravitacional corresponde ao centro do paralelepípedo que modela o casco. Se fixarmos o sistema de coordenadas sobre a superfície da água, la altura do centro de massa ($z_G$) será dado subtraindo o rascunho de objeto ($d$) de la meia altura do paralelepípedo ($c$):
| $ z_G = c - d $ |
ID:(11966, 0)
Posição do metacentro do paralelepípedo
Equação
O cálculo de la altura do metacentro ($z_M$) a partir da distância entre o metacentro e o centro de massa da água deslocada, expressa por o meia largura do paralelepípedo ($b$) e o rascunho de objeto ($d$), é realizado da seguinte forma:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11973, 0)
Condição de estabilidade
Equação
Para que o objeto seja estável, la altura do metacentro ($z_M$) deve sempre ser maior ou igual a la altura do centro de massa ($z_G$).
Portanto, deve ser:
| $ z_M \geq z_G $ |
ID:(11974, 0)
Condição de estabilidade para o paralelepípedo
Equação
Para um paralelepípedo retangular, la condição de estabilidade de um corpo flutuante ($e$) com o meia largura do paralelepípedo ($b$), la meia altura do paralelepípedo ($c$) e o rascunho de objeto ($d$) é:
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
Para que o paralelepípedo seja estável, la altura do metacentro ($z_M$) deve sempre ser maior ou igual a la altura do centro de massa ($z_G$), ou seja,
| $ z_M \geq z_G $ |
Portanto, com la altura do centro de massa ($z_G$) sendo o ponto de aplicação da força de flutuação fornecida com la meia altura do paralelepípedo ($c$) e o rascunho de objeto ($d$):
| $ z_G = c - d $ |
e la altura do metacentro ($z_M$) sendo com o meia largura do paralelepípedo ($b$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
obtemos la condição de estabilidade de um corpo flutuante ($e$):
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
sendo maior que um no caso de uma situação estável e negativo no caso de instabilidade.
ID:(11975, 0)