Usuario:
Estabilidad de la flotación
Storyboard 
La fuerza generada por la flotación actúa en el centro del volumen desplazado, que generalmente está más bajo que el centro de masa del objeto en el agua. Esta pareja de fuerzas implica la generación de momentos de torsión que pueden estabilizar o desestabilizar el objeto. En el segundo caso, incluso podría terminar volteándose. Este principio se aplica tanto a objetos inanimados como a seres vivos que, debido a enfermedades, pueden tener dificultades para mantenerse verticales.
ID:(1610, 0)
Mecanismos
Iframe
Mecanismos
ID:(15481, 0)
La catástrofe del Vasa
Descripción
El barco de guerra sueco Vasa es un ejemplo conocido de un barco inestable. El 10 de agosto de 1628, apenas 20 minutos después de haber zarpado del astillero en su viaje inaugural en el puerto de Estocolmo, el barco se volcó y se hundió:
El diseño del barco era defectuoso, ya que su diseño estrecho estaba destinado a alcanzar altas velocidades y su estructura alta estaba diseñada para acomodar 64 cañones, un número significativo. Sin embargo, este diseño hizo que el barco fuera inherentemente inestable, lo que llevó a su volcamiento con la primera ráfaga de viento.
Afortunadamente, el barco se hundió en aguas poco profundas y se conservó en el agua salada durante 333 años hasta su recuperación en 1961. Inicialmente, el barco se mantuvo húmedo y luego se reemplazó lentamente el agua con una mezcla de cera que permitió exhibirlo completamente seco en un museo a pocos metros de donde se hundió.
El Vasa sirve como una historia de precaución en la construcción naval, demostrando la importancia de un diseño cuidadoso y la estabilidad. Su exhibición en el museo es una atracción popular, atrayendo a visitantes de todo el mundo para ver esta notable pieza de la historia marítima.
ID:(11977, 0)
Punto de ataque de la flotación
Descripción
El punto de aplicación de la fuerza de empuje es igual al centro de masa del volumen de líquido desplazado:
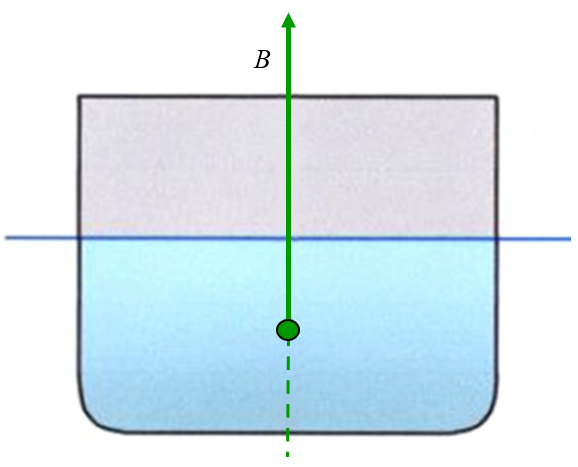
En un barco típico de perfil cuadrado, esto corresponde a un punto ubicado a mitad de calado (profundidad de inmersión).
ID:(11957, 0)
Definir el metacentro
Descripción
Si se aplica una fuerza lateral y se inclina el objeto, se observa que el punto en el que actúa la fuerza de flotación se desplaza fuera del eje. Si se dibuja una línea vertical desde esta nueva posición, se obtiene que la línea se cruza con el eje central en un punto que llamamos metacentro:
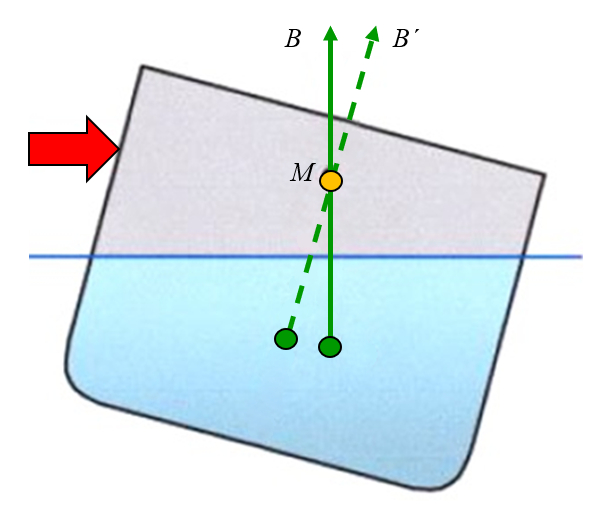
ID:(11959, 0)
Acción de la gravedad
Concepto
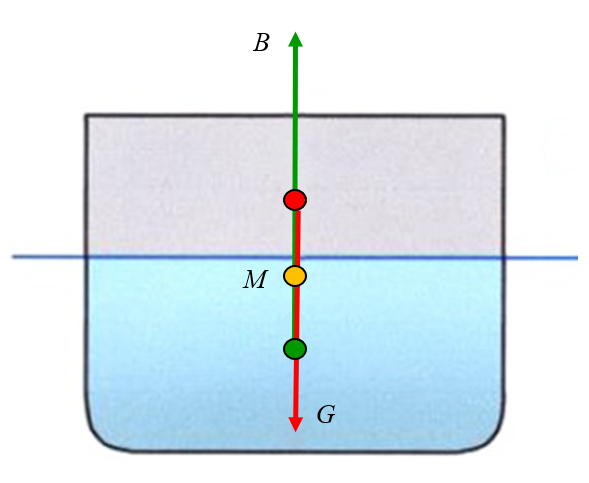
La gravedad actúa sobre el centro de masa, que generalmente se encuentra sobre el punto de aplicación de la fuerza de flotación, pero puede estar por encima o por debajo del metacentro:
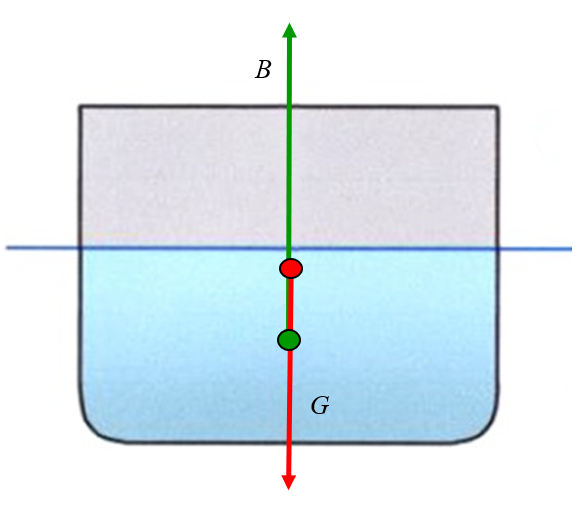
ID:(11960, 0)
Situación estable
Descripción
Si el metacentro está por encima del centro de masa, la fuerza de la gravedad genera un torque que tiende a estabilizar el objeto. Es como si el objeto estuviera colgado del metacentro y la fuerza de la gravedad generara rotaciones en torno a él. Cuando el centro de masa está por debajo del metacentro, el torque genera una rotación hacia el eje, es decir, tiende a corregir el ladeo y, por lo tanto, a estabilizar el objeto:
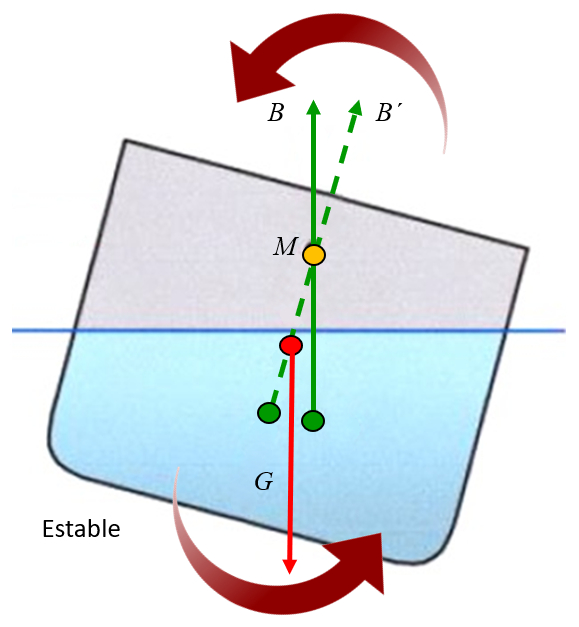
ID:(11961, 0)
Metacentro debajo de centro de gravedad
Descripción
Si el metacentro puede estar sobre o debajo del centro de gravedad. Esto ultimo puede fácilmente ocurrir si se agrega carga en la parte superior haciendo subir el centro de masa lo que lleva a que el sistema se vuelve inestable.
Nota: para evitar perder la estabilidad es importante posicionar la carga en una posición baja (fondo del barco).
ID:(11962, 0)
Situación inestable
Descripción
Si el metacentro está por debajo del centro de masa, la fuerza de la gravedad genera un torque que tiende a desestabilizar el objeto. Es como si el objeto estuviera colgado del metacentro y la fuerza de la gravedad generara rotaciones en torno a él. Cuando el centro de masa está por encima del metacentro, el torque genera una rotación alejándolo del eje, es decir, tiende a aumentar la inclinación y, por lo tanto, a desestabilizar el objeto:
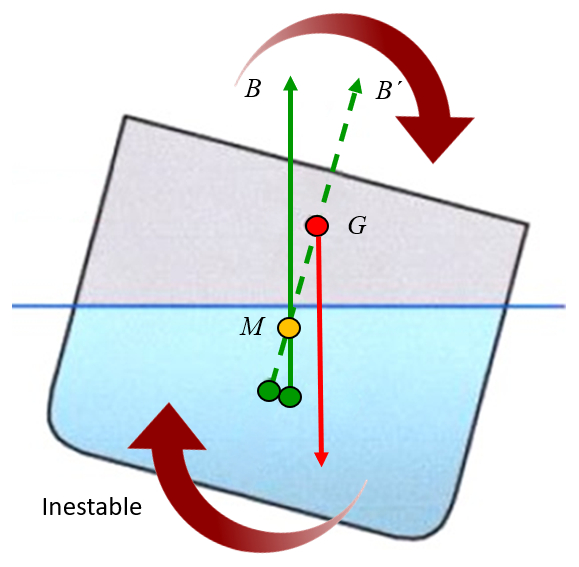
ID:(11963, 0)
Modelo del casco de un barco
Descripción
El modelo del casco del barco se reduce a un paralelepípedo el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y la media altura del paralelepípedo ($c$), con consiguientes dimensiones de $2a \times 2b \times 2c$ y con un calado del objeto ($d$):
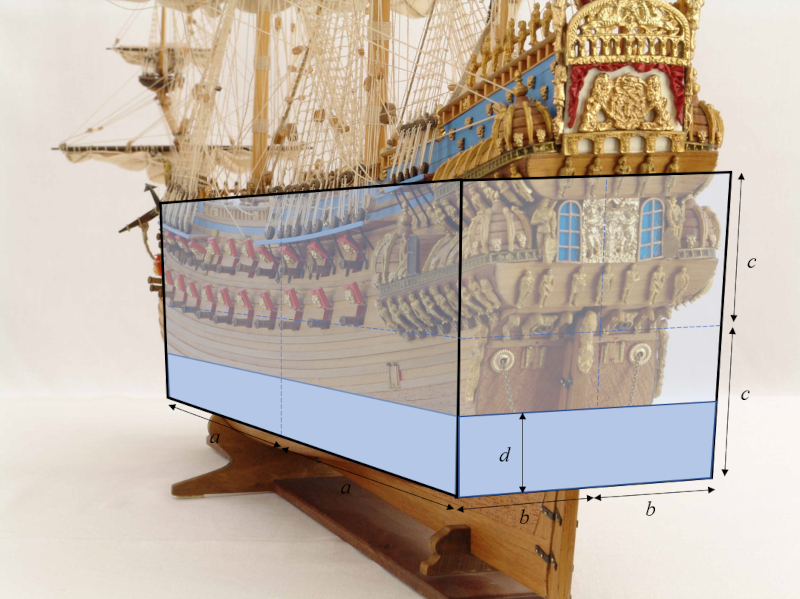
ID:(11969, 0)
Modelo simplificado: paralelepípedo recto
Concepto
Un modelo utilizado para los barcos es el de un paralelepípedo recto con longitudes de el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y la media altura del paralelepípedo ($c$), y un centro de masa en su centro geométrico. Al ser colocado en el agua, el cuerpo se sumerge hasta una profundidad de un calado del objeto ($d$). La posición del centro en la que actúa la fuerza de flotación se muestra en la siguiente imagen, con coordenadas la altura punto de ataque fuerza de flotación ($z_B$), la altura del centro de masa ($z_G$) y la altura del metacentro ($z_M$):
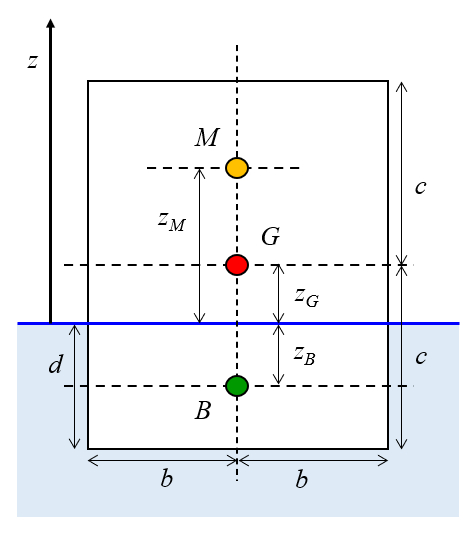
Por ello la altura del centro de masa ($z_G$) es
| $ z_G = c - d $ |
ID:(11964, 0)
Definición de la posición del metacentro
Descripción
El metacentro se calcula determinando el centro de masa del cuerpo inclinado bajo la condición de que el área debajo de la línea de flotación (línea azul) sea constante:
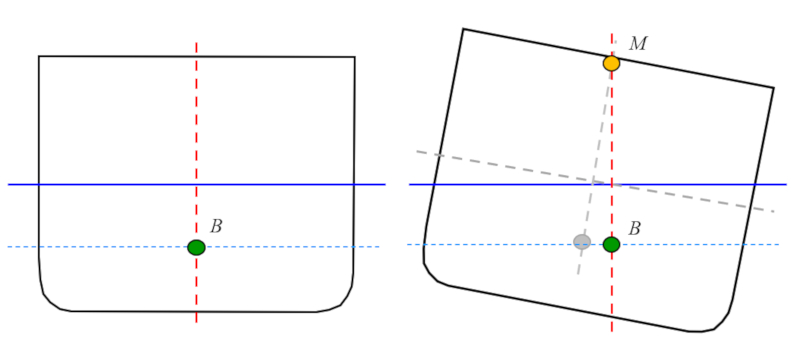
ID:(11979, 0)
Cálculo de la posición del centro de masa del agua desplazada
Descripción
Cuando el barco está escorado se desplaza una sección mayor de agua en un lado y por la misma sección menor en el lado opuesto. El centro de masa se desplaza por ello del centro al sector con mayor desplazamiento que se calcula mediante
$\bar{x} = \displaystyle\frac{\displaystyle\sum_i m_i x_i}{\displaystyle\sum_i m_i}$
La masa es proporcional a la sección que se calcula de el medio ancho del paralelepípedo ($b$) y el calado del objeto ($d$) mediante:
$2b d$
Todas las masas que se compensan a ambos lados del eje no contribuyen al numerador y solo los dos triángulos indicados de un área con el ángulo de escora ($\phi$)
$b^2\phi$
ponderan la posición del centro de masa de los triángulos
$\displaystyle\frac{2b}{3}$
lo que se observa en la grafica:
Por ello la distancia del centro de masa del agua desplazada del eje es
$\displaystyle\frac{\displaystyle\frac{2b}{3} b^2\phi}{2bd}=\displaystyle\frac{b^2\phi}{3d}$
ID:(14248, 0)
Cálculo de la posición del metacentro
Descripción
Si un barco se escora en el ángulo de escora ($\phi$), el centro de masa del agua desplazada se mueve con el medio ancho del paralelepípedo ($b$) y el medio largo del paralelepípedo ($a$) se obtiene una distancia de:
$\displaystyle\frac{b^2\phi}{3d}$
Como esta distancia es el arco del círculo que se puede trazar alrededor del metacentro, la distancia entre el metacentro y el centro de masa del agua desplazada, que corresponde al radio, es:
$\displaystyle\frac{b^2}{3d}$
Por lo tanto, la posición del metacentro debe tener en cuenta que el centro de coordenadas se encuentra a la altura de la superficie del agua, que está a una distancia de $d/2$ por encima del centro de masa del agua desplazada:
con la altura del metacentro ($z_M$):
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11967, 0)
Análisis de la condición de estabilidad para el paralelepípedo
Descripción
Para que el paralelepípedo sea estable, la altura del metacentro ($z_M$) siempre debe ser mayor o igual que la altura del centro de masa ($z_G$), es decir
| $ z_M \geq z_G $ |
Por lo tanto, con la altura del centro de masa ($z_G$) del punto de aplicación de la fuerza de flotación dada es con la media altura del paralelepípedo ($c$) y el calado del objeto ($d$):
| $ z_G = c - d $ |
y la altura del metacentro ($z_M$) es con el medio ancho del paralelepípedo ($b$)
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
se obtiene la condición de estabilidad de un cuerpo que flota ($e$):
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
lo que significa que existe una región en la gráfica $b/c$ (ancho/calado) versus $d/2c$ (calado/altura) en la que el sistema es estable, y en su complemento, inestable:
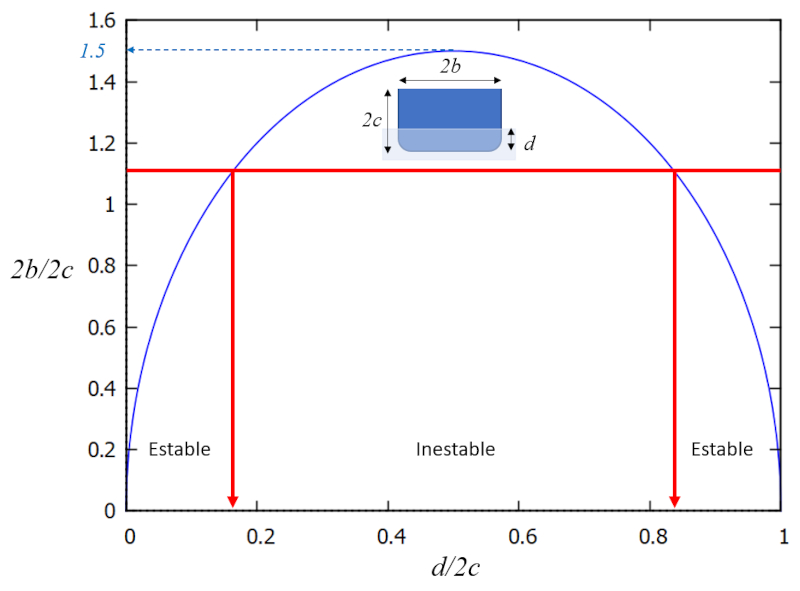
En otras palabras, la estabilidad se logra con valores grandes de $b/c$ (ancho mayor que el calado). En el caso del barco Vasa, el problema era que el barco era demasiado alto para su anchura. Una solución habría sido 'hundirlo más', o lograr un valor de $d/c$ mayor para evitar la zona de inestabilidad. Sin embargo, esto no era posible debido a las aperturas para los cañones a través de las cuales habría entrado agua.
Para obtener más información sobre los errores de construcción, consulte Why The Vasa Sank: 10 Problems and Some Antidotes for Software Projects, Richard E. Fairley, Mary Jane Willshire, marzo/abril de 2003 IEEE SOFTWARE, que se aplica a proyectos de software.
ID:(11976, 0)
Análisis del caso de la Wasa
Descripción
Al estudiar los planos del Vasa, es posible estimar los coeficientes de la relación entre el ancho y la altura, así como entre el calado y la altura. Este análisis revela que el navío es inestable:
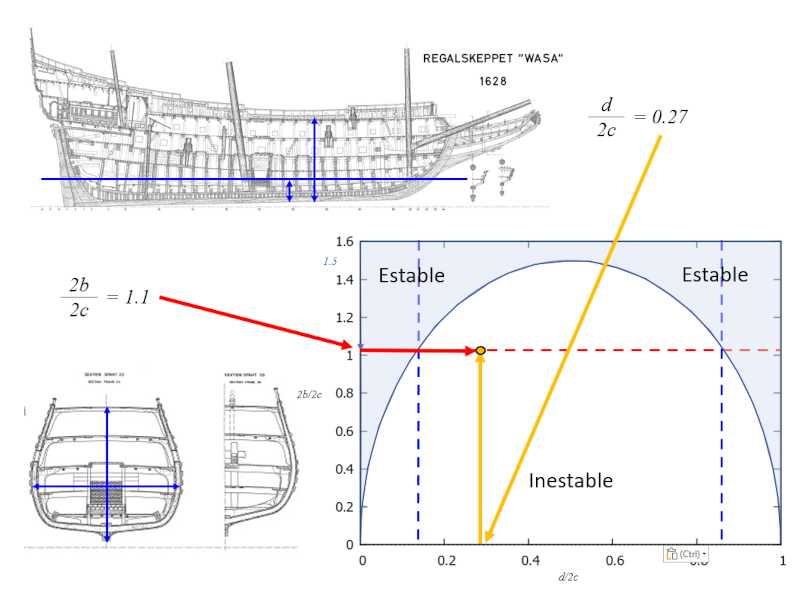
ID:(14247, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$
e = b ^2/(6* c ^2) - d *(1 - d /(2* c ))/(2* c )
$ M_b = M_s $
M_b = M_s
$ M_b =4 a b d \rho_w $
M_b =4* a * b * d * rho_w
$ M_s =8 a b c \rho_s $
M_s =8* a * b * c * rho_s
$ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$
rho_s / rho_w = d /(2* c )
$ V_b = 4 a b d $
V_b = 4 * a * b * d
$ z_B =-\displaystyle\frac{ d }{2}$
z_B =- d /2
$ z_G = c - d $
z_G = c - d
$ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$
z_M =- d /2 + b ^2/(3* d )
$ z_M \geq z_G $
z_M >= z_G
ID:(15483, 0)
Flotación, en función de la masa
Ecuación
Si la fuerza de flotación ($F_b$) y la fuerza gravitacional ($F_g$) son iguales, el objeto flotará. En este caso, esto significa que la masa del objeto que flota ($M_s$) debe ser igual a la masa de líquido desplazado ($M_b$), lo que da como resultado:
| $ M_b = M_s $ |
La fuerza de flotación ($F_b$) está determinada por la densidad del líquido ($\rho_w$), el volumen desplazado ($V_b$) y la aceleración gravitacional ($g$) como:
| $ F_b = \rho_w V_b g $ |
lo cual se opone a la fuerza gravitacional ($F_g$) con la masa del objeto que flota ($M_s$) según:
| $ F_g = m_g g $ |
por lo tanto, con la masa de líquido desplazado ($M_b$) y la masa del objeto que flota ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
se tiene que
| $ M_b = M_s $ |
Nota: esta relación solo es posible si el objeto 'pesa menos que el agua', lo que significa que el agua desplazada ocupa un volumen igual o mayor que el del objeto.
ID:(11955, 0)
Masa del objeto
Ecuación
La masa del objeto que flota ($M_s$) se puede calcular a partir de la densidad del objeto ($\rho_s$) y el volumen dado por sus parámetros geométricos el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y la media altura del paralelepípedo ($c$).
Por lo tanto:
| $ M_s =8 a b c \rho_s $ |
ID:(11970, 0)
Masa del agua desplazada en barco modelo
Ecuación
La masa de líquido desplazado ($M_b$) se puede calcular de la densidad del líquido ($\rho_w$) y el volumen dado por sus parámetros geométricos el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y el calado del objeto ($d$).
Por lo tanto:
| $ M_b =4 a b d \rho_w $ |
ID:(11971, 0)
Volumen desplazado
Ecuación
El volumen desplazado ($V_b$) se puede calcular de sus parámetros geométricos el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y el calado del objeto ($d$).
Por lo tanto:
| $ V_b = 4 a b d $ |
ID:(11968, 0)
Principio de Arquimedes para el paralelepípedo
Ecuación
El principio de Arquímedes establece que la masa de agua desplazada es igual a la masa del objeto. Para el caso específico del paralelepípedo recto, esto se puede expresar como la densidad del objeto ($\rho_s$), la densidad del líquido ($\rho_w$), el calado del objeto ($d$) y la media altura del paralelepípedo ($c$) de la siguiente manera:
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
Dado que el principio de Arquímedes establece que la masa de líquido desplazado ($M_b$) es igual a la masa del objeto que flota ($M_s$),
| $ M_b = M_s $ |
se deduce que la masa de líquido desplazado ($M_b$) está relacionado con la densidad del líquido ($\rho_w$), el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y el calado del objeto ($d$) de la siguiente manera:
| $ M_b =4 a b d \rho_w $ |
y la masa del objeto que flota ($M_s$) está relacionado con la densidad del objeto ($\rho_s$), el medio largo del paralelepípedo ($a$), el medio ancho del paralelepípedo ($b$) y la media altura del paralelepípedo ($c$) de esta manera:
| $ M_s =8 a b c \rho_s $ |
lo que implica que
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
ID:(11972, 0)
Posición del punto de ataque de la fuerza de flotación
Ecuación
El punto en el que actúa la fuerza de flotación se encuentra en el centro de masa del volumen de agua desplazada por el barco. En el caso de que el barco no esté inclinado (escorado), este punto está ubicado en el centro del volumen a media altura del calado.
Teniendo esto en cuenta, se puede expresar la altura punto de ataque fuerza de flotación ($z_B$) en función de el calado del objeto ($d$) es:
| $ z_B =-\displaystyle\frac{ d }{2}$ |
ID:(11965, 0)
Posición del punto de ataque de la fuerza gravitacional
Ecuación
El punto de aplicación de la fuerza gravitatoria corresponde al centro del paralelepípedo que modela el casco. Si se establece el sistema de coordenadas sobre la superficie del agua, la altura del centro de masa ($z_G$) se obtendrá restando el calado del objeto ($d$) a la media altura del paralelepípedo ($c$):
| $ z_G = c - d $ |
ID:(11966, 0)
Posición del metacentro para el paralelepípedo
Ecuación
Se calcula la altura del metacentro ($z_M$) a partir de la distancia entre el metacentro y el centro de masa del agua desplazada, que se expresa con el medio ancho del paralelepípedo ($b$) y el calado del objeto ($d$), como sigue:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11973, 0)
Condición de estabilidad
Ecuación
Para que el objeto sea estable, la altura del metacentro ($z_M$) siempre debe ser mayor o igual que la altura del centro de masa ($z_G$).
Por lo tanto, debe ser:
| $ z_M \geq z_G $ |
ID:(11974, 0)
Condición de estabilidad para el paralelepípedo
Ecuación
Para un paralelepípedo rectangular, la condición de estabilidad de un cuerpo que flota ($e$) con el medio ancho del paralelepípedo ($b$), la media altura del paralelepípedo ($c$) y el calado del objeto ($d$) es igual a:
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
Para que el paralelepípedo sea estable, la altura del metacentro ($z_M$) siempre debe ser mayor o igual que la altura del centro de masa ($z_G$), es decir
| $ z_M \geq z_G $ |
Por lo tanto, con la altura del centro de masa ($z_G$) del punto de aplicación de la fuerza de flotación dada es con la media altura del paralelepípedo ($c$) y el calado del objeto ($d$):
| $ z_G = c - d $ |
y la altura del metacentro ($z_M$) es con el medio ancho del paralelepípedo ($b$)
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
se obtiene la condición de estabilidad de un cuerpo que flota ($e$):
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
siendo mayor que uno en el caso de una situación estable y negativo en el caso de inestabilidad.
ID:(11975, 0)